Các kiểu dữ liệu trong C ( int - float - double - char ...) 
Thuật toán tìm ước chung lớn nhất trong C/C++ 
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành) 
ComboBox - ListBox trong lập trình C# winforms 
Random trong Python: Tạo số random ngẫu nhiên 
Lệnh cin và cout trong C++ 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Thêm Node mới vào cây đỏ đen
Trong bài này mình sẽ giới thiệu đến các bạn cách thêm một Node mới vào cây đỏ đen. Đây là một trong các thao tác cơ bản nhưng rất quan trọng của các cấu trúc dữ liệu nói chung và cây đỏ đen nói riêng.
Chúng ta sẽ cùng nhau tìm hiểu về cách thêm một Node mới như thế nào, sau đó thực hiện một ví dụ thêm Node vào cây đỏ đen.
1. Thêm Node mới vào cây đỏ đen
Việc thêm một Node mới vào cây đỏ đen tương tự như cây nhị phân tìm kiếm, vì bản chất nó là một cây nhị phân tìm kiếm.
- Thực hiện thêm Node như cây nhị phân tìm kiếm.
- Node mới thêm vào luôn luôn có màu đỏ.
- Nếu xảy ra vi phạm quy tắc thì thực hiện điều chỉnh cây.
Khi chúng ta thêm một Node mới là Node đỏ vào cây đỏ đen, có thể sẽ vi phạm một số quy tắc sau:
Bài viết này được đăng tại [free tuts .net]
- Node gốc là Node đen: Khi chúng ta thêm Node đỏ vào cây đỏ đen, mà Node cần thêm đó chính là Node gốc thì khi đó sẽ vi phạm quy tắc số 1 (Node gốc luôn luôn là Node đẹn).
- Xảy ra xung đột đỏ - đỏ: Khi chúng ta thêm một Node đỏ vào cây đỏ đen, mà Node cha của nó cũng là Node đó thì khi đó sẽ xảy ra xung đột đỏ - đỏ.
Như vậy khi ta thêm một Node vào cây đỏ đen có thể làm thay đổi quy tắc của nó, vì vậy chúng ta cần điều chỉnh nó ngay sau khi thêm vào cây. Để làm được điều này, các bạn hãy xem các trường hợp có thể xảy ra ở mục tiếp theo.
2. Điều chỉnh cây vi phạm quy tắc khi thêm Node
Trong phần này mình sẽ đưa ra các trường hợp có thể xảy ra làm thay đổi quy tắc của cây đỏ đen, cụ thể sẽ có 5 trường hợp và mỗi trường hợp mình sẽ có một đoạn code C++.
Trước khi bắt đầu các trường hợp mình có một số ký hiệu để dễ thực hiện hơn như sau:
- N dùng để chỉ Node đang chèn vào.
- P chỉ Node cha của N.
- G chỉ Node ông của N.
- U chỉ Node chú và bác của N.
Trường hợp 1
Node N mới thêm vào ngay tại Node gốc. Trong trường hơp này, gán lại màu đen cho N để đảm bảo tính chất 2 (Gốc luôn luôn đen). Vì mới chỉ bổ sung một nút nên tính chất 5 được bảo đảm vì mọi đường đi chỉ có một nút.
void insert_case1(struct node *n) {
if (n->parent == NULL)
n->color = BLACK;
else insert_case2(n);
}Trường hợp 2
Nút cha P của nút mới thêm là đen, khi đó Tính chất 4 (Cả hai nút con của nút đỏ là đen) không bị vi phạm vì nút mới thêm có hai con là "null' là đen. Tính chất 5 cũng không vi phạm vì nút mới thêm là đỏ không ảnh hưởng tới số nút đen trên tất cả đường đi.
void insert_case2(struct node *n) {
if (n->parent->color== BLACK)
return;
else
insert_case3(n);
} Trường hợp 3
Khi Node cha P và Node chú U có màu đỏ và Node ông G có màu đen, thì ta thực hiện đổi cả hai Node P và U thành đen và G thành đỏ (để đảm bảo quy tắc số 5). Tuy nhiên khi đổi như vậy có thể Node G vi phạm quy tắc số 2 (Node gốc luôn đen), để khắc phục ta thực hiện gọi đệ quy trên G từ trường hợp 1.
void insert_case3(struct node *n) {
if (uncle(n) != NULL && uncle(n)->color == RED) {
n->parent->color = BLACK;
uncle(n)->color = BLACK; grandparent(n)->color = RED;
insert_case1(grandparent(n));
}
else insert_case4(n);
}Trường hợp 4
Nút cha P là đỏ nhưng nút chú bác U là đen, nút mới N là con phải của nút P, và P là con trái của nút G. Trong trường hợp này, thực hiện quay trái chuyển đổi vai trò của nút mới N và nút cha P.
void insert_case4(struct node *n) {
if (n == n->parent->right && n->parent == grandparent(n)->left) {
rotate_left(n->parent); n = n->left; }
else if (n == n->parent->left && n->parent == grandparent(n)->right) {
otate_right(n->parent); n = n->right;
}
insert_case5(n);
}Trường hợp 5
Nút cha P là đỏ nhưng nút bác U là đen, nút mới N là con trái của nút P, và P là con trái của nút ông G. Trong trường hợp này, một phép quay phải trên nút ông G được thực hiện.
void insert_case5(struct node *n) {
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left) {
rotate_right(grandparent(n)); }
else {
rotate_left(grandparent(n));
}
}3. Ví dụ thêm Node mới vào cây đỏ đen
Trong ví dụ này mình sẽ thực hiện thêm vào một số Node là các số nguyên, sau đó thực hiện xuất nó ra màn hình.
#include <iostream>
using namespace std;
/* khai báo thuộc tính color */
enum Color {RED, BLACK};
/* khai báo cấu trúc node */
struct Node
{
int data;
bool color;
Node *left, *right, *parent;
// Constructor
Node(int data)
{
this->data = data;
left = right = parent = NULL;
this->color = RED;
}
};
/* class đại diện cho cây đỏ-đen */
class RBTree
{
private:
Node *root;
protected:
void rotateLeft(Node *&, Node *&);
void rotateRight(Node *&, Node *&);
void fixViolation(Node *&, Node *&);
public:
/* Constructor */
RBTree() { root = NULL; }
void insert(const int &n);
void inorder();
// void levelOrder();
};
/* Một hàm đệ quy để thực hiện việc duyệt thứ tự cấp độ */
void inorderHelper(Node *root)
{
if (root == NULL)
return;
inorderHelper(root->left);
cout << root->data << " ";
inorderHelper(root->right);
}
/* insert Node */
Node* BSTInsert(Node* root, Node *pt)
{
/* Nếu cây trống thì trả về một Node mới */
if (root == NULL)
return pt;
/* Nếu không thì tiếp tục duyệt xuống dưới cây */
if (pt->data < root->data)
{
root->left = BSTInsert(root->left, pt);
root->left->parent = root;
}
else if (pt->data > root->data)
{
root->right = BSTInsert(root->right, pt);
root->right->parent = root;
}
/* trả về con trỏ Node */
return root;
}
/* thuật toán xoay trái */
void RBTree::rotateLeft(Node *&root, Node *&pt)
{
Node *pt_right = pt->right;
pt->right = pt_right->left;
if (pt->right != NULL)
pt->right->parent = pt;
pt_right->parent = pt->parent;
if (pt->parent == NULL)
root = pt_right;
else if (pt == pt->parent->left)
pt->parent->left = pt_right;
else
pt->parent->right = pt_right;
pt_right->left = pt;
pt->parent = pt_right;
}
/*thuật toán xoay phải*/
void RBTree::rotateRight(Node *&root, Node *&pt)
{
Node *pt_left = pt->left;
pt->left = pt_left->right;
if (pt->left != NULL)
pt->left->parent = pt;
pt_left->parent = pt->parent;
if (pt->parent == NULL)
root = pt_left;
else if (pt == pt->parent->left)
pt->parent->left = pt_left;
else
pt->parent->right = pt_left;
pt_left->right = pt;
pt->parent = pt_left;
}
/* sửa lại cấu trúc khi chèn Node vào hoặc xóa node */
void RBTree::fixViolation(Node *&root, Node *&pt)
{
Node *parent_pt = NULL;
Node *grand_parent_pt = NULL;
while ((pt != root) && (pt->color != BLACK) &&
(pt->parent->color == RED))
{
parent_pt = pt->parent;
grand_parent_pt = pt->parent->parent;
/* trường hợp A:
Node cha của pt là con trái của Node cha của pt */
if (parent_pt == grand_parent_pt->left)
{
Node *uncle_pt = grand_parent_pt->right;
/* trường hợp : 1
Node chú của pt là Node đỏ khi này chỉ cần đổi màu cho Node đó thành đen */
if (uncle_pt != NULL && uncle_pt->color == RED)
{
grand_parent_pt->color = RED;
parent_pt->color = BLACK;
uncle_pt->color = BLACK;
pt = grand_parent_pt;
}
else
{
/* trường hợp : 2
pt là Node con phải của Node cha nó ta thực hiện xoay trái*/
if (pt == parent_pt->right)
{
rotateLeft(root, parent_pt);
pt = parent_pt;
parent_pt = pt->parent;
}
/* trường hợp : 3
pt là con trái của node cha nó ta thực hiện xoay phải */
rotateRight(root, grand_parent_pt);
swap(parent_pt->color, grand_parent_pt->color);
pt = parent_pt;
}
}
/* trường hợp : B
Node cha của pt là con phải của Node cha của pt */
else
{
Node *uncle_pt = grand_parent_pt->left;
/* trường hợp : 1
Node chú của pt là Node đỏ khi này chỉ cần đổi màu cho Node đó thành đen */
if ((uncle_pt != NULL) && (uncle_pt->color == RED))
{
grand_parent_pt->color = RED;
parent_pt->color = BLACK;
uncle_pt->color = BLACK;
pt = grand_parent_pt;
}
else
{
/* Case : 2
pt là con trái của node cha nó ta thực hiện xoay phải */
if (pt == parent_pt->left)
{
rotateRight(root, parent_pt);
pt = parent_pt;
parent_pt = pt->parent;
}
/* Case : 3
pt là Node con phải của Node cha nó ta thực hiện xoay trái */
rotateLeft(root, grand_parent_pt);
swap(parent_pt->color, grand_parent_pt->color);
pt = parent_pt;
}
}
}
root->color = BLACK;
}
/* chèn một Node mới với dữ liệu đã cho */
void RBTree::insert(const int &data)
{
Node *pt = new Node(data);
/* thực hiện chèn như bình thường */
root = BSTInsert(root, pt);
/* sửa lại lỗi của quy tắc cây đỏ đen */
fixViolation(root, pt);
}
void RBTree::inorder() { inorderHelper(root);}
/* hàm main để thực hiện kiểm tra kết quả */
int main()
{
RBTree tree;
tree.insert(7);
tree.insert(6);
tree.insert(5);
tree.insert(4);
tree.insert(3);
tree.insert(2);
tree.insert(1);
cout << "Output: \n";
tree.inorder();
cout<<"\n-------------------------------------\n";
cout<<"Chương trình này được đăng tại Freetuts.net";
}
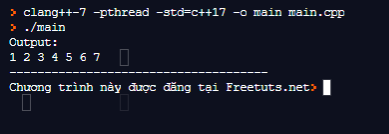
Kết quả: Với input là 7, 6, 5, 4, 3, 2, 1.
4. Kết luận
Như vậy chúng ta đã tìm hiểu xong cách thêm một Node vào cây đỏ đen, cũng như các trường hợp và cách khắc phục khi bị vi phạm một số quy tắc của cây đỏ đen. Ở bài tiếp theo mình sẽ thực hiện xóa Node khỏi cây đỏ đen, các bạn chú ý theo dõi nhé !!!
