Xóa Node khỏi cây nhị phân tìm kiếm
Trong hướng dẫn này mình sẽ giới thiệu các bạn cách xóa một Node bất kì khỏi cây nhị phân tìm kiếm. Đây là một thao tác rất quan trong và đòi hỏi các bạn phải nắm vững kiến thức về C++ cũng như cấu trúc dữ liệu cây.

Chúng ta sẽ cùng nhau thực hiện xóa Node có 1 con, Node có 2 con và Node lá trong cây nhị phân tìm kiếm.
1. Xoá Node có một con và Node lá
Việc xóa Node có một con và Node lá được thực hiện khá đơn giản, cụ thể như sau:
Việc đầu tiên ta cần kiểm tra xem cây có tồn tại phần tử hay không, nếu không tồn tại ta return rồi kết thúc hàm, ngược lại nếu tồn tại phần tử ta bắt đầu duyệt sang cây con trái và cây con phải để tìm phần tử cần xóa.
Bài viết này được đăng tại [free tuts .net]
Nếu như data nhỏ hơn Node gốc thì ta duyệt sang nhánh trái của cây và nếu data lớn hơn Node gốc thì ta duyệt qua nhánh phải của cây.
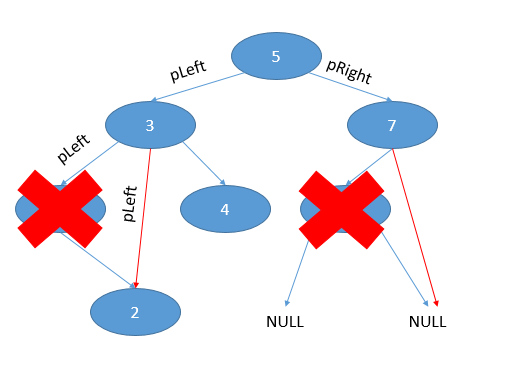
Sau khi tìm được giá trị cần xóa, khi này ta cần cập nhật lại mối liên kết trước khi bắt đầu tiến hành xóa Node. Ta sẽ tạo một Node *X = t (X là Node thế mạng, lát nữa ta sẽ xóa nó).
Trong trường hợp Node có một con sẽ có hai trường hợp khác đó chính là Node có cây con trái và Node cây con phải.
- Nếu Node có một cây con trái thì ta thực hiện duyệt sang trái để cập nhật lại mối liên kết giữa Node cha và Node con của Node cần xóa
- Nếu Node có một cây con phải thì ta thực hiện duyệt sang phải để cập nhật lại mối liên kết giữa Node cha và Node con của Node cần xóa.
Sau khi cập nhật xong mối liên kết giữa Node cần xóa với các Node con và Node cha, thì ta sẽ thực hiện xóa Node đó.
*Lưu ý: Trong trường hợp xóa Node có một con, hệ quả của nó có thể dùng để xóa Node lá luôn, bởi vì Node lá là Node không tồn tại cây con trái và cây con phải. Vì vậy khi cập nhật lại mối liên kết thì cây con trái hay cây con phải đều bằng NULL.
void XoaNode(TREE &t, int data) // data chính là giá trị của cái node cần xóa
{
// nếu như cây đang rỗng
if (t == NULL)
{
return; // kết thúc hàm
}
else
{
// nếu như data nhỏ hơn node gốc
if (data < t->data)
{
XoaNode(t->pLeft, data); // duyệt sang nhánh trái của cây
}
else if (data > t->data)
{
XoaNode(t->pRight, data); // duyệt sang nhánh phải của cây
}
else // data == t->data - đã tìm ra cái node cần xóa
{
NODE *X = t; // node X là node thế mạng - tí nữa chúng ta sẽ xóa nó
// nếu như nhánh trái bằng NULL <=> đây là cây có 1 con chính là con phải
if (t->pLeft == NULL)
{
// duyệt sang phải của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pRight;
}
else if (t->pRight == NULL)
{
// duyệt sang trái của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pLeft;
}
delete X; // xóa node cần xóa
}
}
}2. Xóa Node có hai con
Trường hợp xóa Node có hai con về cơ bản thì phức tạp hơn cách xóa Node có một con và Node lá, nhưng nếu như các bạn nắm được bản chất của nó thì cũng sẽ rất đơn giản.
Trước khi xóa một Node có hai con ta cần chiều chỉnh lại mối liên kết giữa Node cần xóa với Node cha và Node con của nó. Để làm được điều này ta cần thực hiện như sau:
- Đầu tiên ta cần tìm ta Node thế mạng cho Node cần xóa, vì khi chúng ta xóa Node X đi thì ta cần bỏ vào đó một Node khác nhưng vẫn thõa mãn cấu trúc dữ liệu cây nhị phân tìm kiếm. Để có được Node thế mạng ta cần tạo một hàm
NodeTheMang()để tìm ra Node có thể thay thế được Node cần xóa. Để tìm được Node này ta sẽ có hai cách: Tìm Node phải nhất bên cây con trái và tìm Node trái nhất của cây con phải. - Sau khi tìm được Node thay thế, ta chỉ cần cập nhật lại data của Node cần xóa chính là data của Node thế mạng. Cũng như cập nhật lại mối liên kết cho Node cha của Node thế mạng và Node con của Node thế mạng.
- Và ở hàm
XoaNode()ngoài hai trường hợp là Node cần xóa là Node có một con và Node lá ra, ta sẽ thêm một trường hợp là Node có hai con rồi gọi đệ quy duyệt sang bên phải (mình đang làm cách tìm Node trái nhất của cây con phải).
Dưới đây là hàm xóa Node bất kì khỏi cây nhị phân tìm kiếm mà mình đã viết, trong đó mình có chú thích rất rõ ràng, các bạn có thể đọc tham khảo nhé.
// hàm tìm node thế mạng
void NodeTheMang(TREE &X, TREE &Y) // NODE Y là node thế mạng cho node cần xóa - node này sẽ đảm nhận nhiệm vụ tìm ra node trái nhất(TÌM NODE TRÁI NHẤT CÂY CON PHẢI) hoặc phải nhất(TÌM NODE PHẢI NHẤT CỦA CÂY CON TRÁI)
{
// CÁCH 1: TÌM NODE TRÁI NHẤT CỦA CÂY CON PHẢI
// duyệt sang bên trái nhất
if (Y->pLeft != NULL)
{
NodeTheMang(X, Y->pLeft);// tìm ra node trái nhất ?
}
else // tìm ra được node trái nhất rồi nek..
{
X->data = Y->data; // cập nhật cái data của node cần xóa chính là data của node thế mạng
X = Y; // cho node X(là node mà chúng ta sẽ đi xóa sau này) trỏ đến node thế mạng ==> ra khỏi hàm thì ta sẽ xóa node X
Y = Y->pRight; // bản chất chỗ này chính là cập nhật lại mối liên kết cho node cha của node thế mạng(mà chúng ta sẽ xóa) với node con của node thế mạng
}
/* CÁCH 2: TÌM NODE PHẢI NHẤT CỦA CÂY CON TRÁI
duyệt sang bên phải
if (Y->pRight != NULL)
{
DiTimNodeTheMang(X, Y->pRight);// tìm ra node phải nhất ?
}
else // tìm ra được node phải nhất rồi nek..
{
X->data = Y->data; // cập nhật cái data của node cần xóa chính là data của node thế mạng
X = Y; // cho node X(là node mà chúng ta sẽ đi xóa sau này) trỏ đến node thế mạng ==> ra khỏi hàm thì ta sẽ xóa node X
Y = Y->pLeft; // bản chất chỗ này chính là cập nhật lại mối liên kết cho node cha của node thế mạng(mà chúng ta sẽ xóa) với node con của node thế mạng
} */
}
// hàm xóa 1 cái node bất kì trong cây nhị phân tìm kiếm
void XoaNode(TREE &t, int data) // data chính là giá trị của cái node cần xóa
{
// nếu như cây đang rỗng
if (t == NULL)
{
return; // kết thúc hàm
}
else
{
// nếu như data nhỏ hơn node gốc
if (data < t->data)
{
XoaNode(t->pLeft, data); // duyệt sang nhánh trái của cây
}
else if (data > t->data)
{
XoaNode(t->pRight, data); // duyệt sang nhánh phải của cây
}
else // data == t->data - đã tìm ra cái node cần xóa
{
NODE *X = t; // node X là node thế mạng - tí nữa chúng ta sẽ xóa nó
// nếu như nhánh trái bằng NULL <=> đây là cây có 1 con chính là con phải
if (t->pLeft == NULL)
{
// duyệt sang phải của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pRight;
}
else if (t->pRight == NULL)
{
// duyệt sang trái của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pLeft;
}
else // node cần xóa là node có 2 con
{
// CÁCH 1: Tìm node trái nhất của cây con phải(cây con phải của cái node cần xóa)
NodeTheMang(X, t->pRight);
// CÁCH 2: Tìm node phải nhất của cây con trái(cây con trái của cái node cần xóa)
//DiTimNodeTheMang(X, t->pLeft);
}
delete X; // xóa node cần xóa
}
}
}3. Ví dụ xóa Node trong cây nhị phân tìm kiếm
Trong ví dụ này mình sẽ thực hiện xóa một Node bất kì trong cây nhị phân tìm kiếm. Để làm được bài toán này ta cần có các hàm khác sau:
- Cấu trúc dữ liệu cây và cấu trúc Node.
- Hàm thêm Node vào cây.
- Hàm duyệt cây.
- Hàm xóa Node khỏi cây.
Full code
#include<iostream>
using namespace std;
// khai báo cấu trúc 1 cái node trong cây nhị phân tìm kiếm
struct node
{
int data; // dữ liệu chứa trong 1 cái node
struct node *pLeft; // con trỏ liên kết với cái node bên trái <=> cây con trái
struct node *pRight; // con trỏ liên kết với cái node bên phải <=> cây con phải
};
typedef struct node NODE;
typedef NODE* TREE;
// hàm khởi tạo cây nhị phân tìm kiếm
void KhoiTaoCay(TREE &t)
{
t = NULL;
}
// hàm thêm 1 cái phần tử vào cây
void ThemNodeVaoCay(TREE &t, int x)
{
// nếu cây rỗng
if (t == NULL)
{
NODE *p = new NODE;
p->data = x;
p->pLeft = NULL;
p->pRight = NULL;
t = p;
}
else
{
// nếu phần tử thêm vào mà nhỏ hơn nút gốc thì sẽ duyệt qua bên trái
if (x < t->data)
{
ThemNodeVaoCay(t->pLeft, x);
}
else if (x > t->data)
{
ThemNodeVaoCay(t->pRight, x);
}
}
}
// hàm xuất phần tử trong cây nhị phân tìm kiếm
void NLR(TREE t)
{
if (t != NULL)
{
// xử lí
cout << t->data << " ";
NLR(t->pLeft);
NLR(t->pRight);
}
}
// hàm tìm node thế mạng
void NodeTheMang(TREE &X, TREE &Y) // NODE Y là node thế mạng cho node cần xóa - node này sẽ đảm nhận nhiệm vụ tìm ra node trái nhất(TÌM NODE TRÁI NHẤT CÂY CON PHẢI) hoặc phải nhất(TÌM NODE PHẢI NHẤT CỦA CÂY CON TRÁI)
{
// CÁCH 1: TÌM NODE TRÁI NHẤT CỦA CÂY CON PHẢI
// duyệt sang bên trái nhất
if (Y->pLeft != NULL)
{
NodeTheMang(X, Y->pLeft);// tìm ra node trái nhất ?
}
else // tìm ra được node trái nhất rồi nek..
{
X->data = Y->data; // cập nhật cái data của node cần xóa chính là data của node thế mạng
X = Y; // cho node X(là node mà chúng ta sẽ đi xóa sau này) trỏ đến node thế mạng ==> ra khỏi hàm thì ta sẽ xóa node X
Y = Y->pRight; // bản chất chỗ này chính là cập nhật lại mối liên kết cho node cha của node thế mạng(mà chúng ta sẽ xóa) với node con của node thế mạng
}
/* CÁCH 2: TÌM NODE PHẢI NHẤT CỦA CÂY CON TRÁI
duyệt sang bên phải
if (Y->pRight != NULL)
{
DiTimNodeTheMang(X, Y->pRight);// tìm ra node phải nhất ?
}
else // tìm ra được node phải nhất rồi nek..
{
X->data = Y->data; // cập nhật cái data của node cần xóa chính là data của node thế mạng
X = Y; // cho node X(là node mà chúng ta sẽ đi xóa sau này) trỏ đến node thế mạng ==> ra khỏi hàm thì ta sẽ xóa node X
Y = Y->pLeft; // bản chất chỗ này chính là cập nhật lại mối liên kết cho node cha của node thế mạng(mà chúng ta sẽ xóa) với node con của node thế mạng
} */
}
// hàm xóa 1 cái node bất kì trong cây nhị phân tìm kiếm
void XoaNode(TREE &t, int data) // data chính là giá trị của cái node cần xóa
{
// nếu như cây đang rỗng
if (t == NULL)
{
return; // kết thúc hàm
}
else
{
// nếu như data nhỏ hơn node gốc
if (data < t->data)
{
XoaNode(t->pLeft, data); // duyệt sang nhánh trái của cây
}
else if (data > t->data)
{
XoaNode(t->pRight, data); // duyệt sang nhánh phải của cây
}
else // data == t->data - đã tìm ra cái node cần xóa
{
NODE *X = t; // node X là node thế mạng - tí nữa chúng ta sẽ xóa nó
// nếu như nhánh trái bằng NULL <=> đây là cây có 1 con chính là con phải
if (t->pLeft == NULL)
{
// duyệt sang phải của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pRight;
}
else if (t->pRight == NULL)
{
// duyệt sang trái của cái node cần xóa để cập nhật mối liên kết giữa node
// cha của node cần xóa với node con của node cần xóa
t = t->pLeft;
}
else // node cần xóa là node có 2 con
{
// CÁCH 1: Tìm node trái nhất của cây con phải(cây con phải của cái node cần xóa)
NodeTheMang(X, t->pRight);
// CÁCH 2: Tìm node phải nhất của cây con trái(cây con trái của cái node cần xóa)
//DiTimNodeTheMang(X, t->pLeft);
}
delete X; // xóa node cần xóa
}
}
}
// hàm nhập cây nhị phân tìm kiếm
void Menu(TREE &t)
{
int luachon;
while(true)
{
cout << "\n\n\t\t ============ MENU ============";
cout << "\n1. Nhập phần tử cho cây";
cout << "\n2. Duyệt cây";
cout << "\n3. Xóa một Node bất kì";
cout << "\n0. Thoát";
cout << "\n\n\t\t ============= END =============";
cout << "\nNhập lựa chọn của bạn: ";
cin >> luachon;
if (luachon == 1)
{
int x;
cout << "\nNhập giá trị: ";
cin >> x;
ThemNodeVaoCay(t, x);
}
else if (luachon == 2)
{
cout << "\nCây nhị phân tìm kiếm\n";
NLR(t);
}
else if (luachon == 3)
{
int x;
cout << "\nNhập giá trị cần xóa: ";
cin >> x;
XoaNode(t, x);
}
else
{
break;
}
}
}
int main()
{
TREE t;
KhoiTaoCay(t);
Menu(t);
cout<<"\n---------------------------------\n";
cout<<"Chương trình này được đăng tại Freetuts.net";
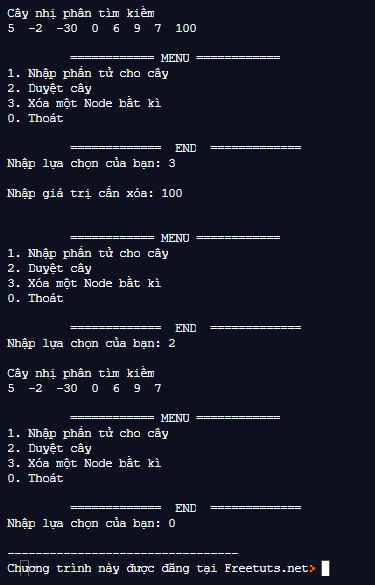
}Kết quả:
Như vậy là chúng ta đã thực hiện xong chương trình xóa một Node bất kì khỏi cây nhị phân tìm kiếm, các bạn có thể thực hiện bài toán này theo nhiều cách khác nhau. Chúc các bạn thực hiện thành công!!!

 Các kiểu dữ liệu trong C ( int - float - double - char ...)
Các kiểu dữ liệu trong C ( int - float - double - char ...)  Thuật toán tìm ước chung lớn nhất trong C/C++
Thuật toán tìm ước chung lớn nhất trong C/C++  Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)  ComboBox - ListBox trong lập trình C# winforms
ComboBox - ListBox trong lập trình C# winforms  Random trong Python: Tạo số random ngẫu nhiên
Random trong Python: Tạo số random ngẫu nhiên  Lệnh cin và cout trong C++
Lệnh cin và cout trong C++  Cách khai báo biến trong PHP, các loại biến thường gặp
Cách khai báo biến trong PHP, các loại biến thường gặp  Download và cài đặt Vertrigo Server
Download và cài đặt Vertrigo Server  Thẻ li trong HTML
Thẻ li trong HTML  Thẻ article trong HTML5
Thẻ article trong HTML5  Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên  Cách dùng thẻ img trong HTML và các thuộc tính của img
Cách dùng thẻ img trong HTML và các thuộc tính của img  Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng