Các kiểu dữ liệu trong C ( int - float - double - char ...) 
Thuật toán tìm ước chung lớn nhất trong C/C++ 
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành) 
ComboBox - ListBox trong lập trình C# winforms 
Random trong Python: Tạo số random ngẫu nhiên 
Lệnh cin và cout trong C++ 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Thuật toán tìm kiếm nội suy (Interpolation Search)
Trong bài này mình sẽ giới thiệu thuật toán Interpolation Search (tìm kiếm nội suy). Đây là một trong những thuật toán tìm kiếm được sử dụng rất nhiều vì tốc độ tìm kiếm rất nhanh và chính xác.
Chúng ta sẽ cùng nhau tìm hiểu về Interpolation Search. Và so sánh nó với Binary Search, để xem sự khác biệt giữa hai cách tìm kiếm này. Sau đó mình sẽ đưa ra thuật toán cho phương pháp tìm kiếm này.
1. Tìm kiếm nội suy là gì?
Thuật toán tìm kiếm nội suy là một sự cải tiến của tìm kiếm nhị phân Binary Search. Nó có xu hướng tiến gần đến vị trí, giá trị tìm kiếm. Do đó tốc độ tìm kiếm được tối ưu rất cao và nhanh hơn nhiều so với Binary Search.
Cách thức hoạt động của nó dựa trên Binary Search, nhưng có sự cải tiến hơn. Đó chính là nó tìm ra phần tử gần với giá trị tìm kiếm nhất và bắt đầu từ đó để tìm.
Bài viết này được đăng tại [free tuts .net]
Ví dụ:
Chúng ta có danh sách các sinh viên trong một lớp. Nếu chúng ta muốn tìm một bạn tên Tiến, thì chúng ta sẽ ưu tiên việc tìm kiếm từ cuối danh sách. Chứ không nên tìm kiếm từ đầu danh sách vì điều đó rất mất thời gian.
Với Interpolation Search nó sẽ linh hoạt hơn rất nhiều trong lúc tìm kiếm.
2. Thuật toán tìm tiếm nội suy (Interpolation Search)
Giả xử chúng ta có:
- Left, right là hai vị trí đầu và cuối.
- T là tập.
- X là giá trị cần tìm.
Giải thích thuật toán
Bước 1:Chúng ta sẽ sử dụng công thức tìm phần tử chính giữa của tập theo cách tìm kiếm Binary Search:
Search = left + (right - left) * 1/2
Trong công thức trên chúng ta sẽ thay giá trị 1/2 bằng biểu thức sau:
(X - T[left]) / (T[right] - T[left])
Sau khi thay biểu thức vào công thức sẽ được công thức mới như sau:
Search = left + (X- T[left]) * (right – left) / (T[right] – T[left])
Bước 2: Bây giờ chúng ta sẽ kiểm tra T[Search] nếu bằng X thì Search chính là vị trí cần tìm.
- Nếu Search < X thì tăng left lên một đơn vị rồi quay lại bước 1.
- Nếu Search > X thì giảm right xuống một đơn vị rồi quay lại bước 1.
Thuật toán tìm kiếm Interpolation Search
int InterPolationSearch(int arr[], int n, int x)
{
int left = 0;
int right = n-1;
while (left <= right && x >= arr[left] && x <= arr[right])
{
double val1 = (double) (x - arr[left]) / (arr[right]-arr[left]);
int val2 = (right-left);
int Search = left + val1*val2;
if (arr[Search] == x)
return Search;
if (arr[Search] < x)
left = Search + 1;
else
right = Search - 1;
}
return -1;
}3. Ví dụ tìm kiếm nội suy
Chúng ta sẽ áp dụng thuật toán trên để tìm một phần tử x trong mảng, được nhập từ bàn phím.
Sau khi đã viết được hàm InterPolationSearch(), thì việc đơn giản của chúng ta sẽ là viết hàm Main và gọi nó ra.
Main:
int main()
{
int arr[] = {10, 12, 13, 16, 18, 19, 20, 21, 22, 23, 24, 33, 35, 42, 47};
int n = sizeof(arr)/sizeof(arr[0]);
int x;
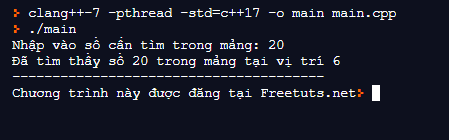
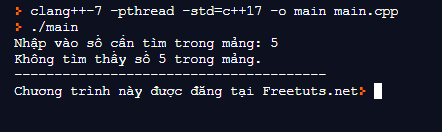
cout<<"Nhập vào số cần tìm trong mảng: ";
cin>>x;
int index = InterPolationSearch(arr, n, x);
if (index != -1)
cout << "Đã tìm thấy số "<<x<< " trong mảng tại vị trí " << index;
else
cout << "Không tìm thấy số "<<x<<" trong mảng.";
}Full Code:
#include <iostream>
using namespace std;
int InterPolationSearch(int arr[], int n, int x)
{
int left = 0;
int right = n-1;
while (left <= right && x >= arr[left] && x <= arr[right])
{
double val1 = (double) (x - arr[left]) / (arr[right]-arr[left]);
int val2 = (right-left);
int Search = left + val1*val2;
if (arr[Search] == x)
return Search;
if (arr[Search] < x)
left = Search + 1;
else
right = Search - 1;
}
return -1;
}
int main()
{
int arr[] = {10, 12, 13, 16, 18, 19, 20, 21, 22, 23, 24, 33, 35, 42, 47};
int n = sizeof(arr)/sizeof(arr[0]);
int x;
cout<<"Nhập vào số cần tìm trong mảng: ";
cin>>x;
int index = InterPolationSearch(arr, n, x);
if (index != -1)
cout << "Đã tìm thấy số "<<x<< " trong mảng tại vị trí " << index;
else
cout << "Không tìm thấy số "<<x<<" trong mảng.";
cout<<"\n---------------------------------------\n";
cout<<"Chương trình này được đăng tại Freetuts.net";
}Kết quả 1:
Kêt quả 2:
Như vậy là chúng ta đã thực hiện xong chương trình kiểm tra một số có trong mảng. Cũng như kết thúc hướng dẫn thuật toán tìm kiếm Interpolatipon Search. Chúc các bạn thực hiện thành công!!!
