Các kiểu dữ liệu trong C ( int - float - double - char ...) 
Thuật toán tìm ước chung lớn nhất trong C/C++ 
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành) 
ComboBox - ListBox trong lập trình C# winforms 
Random trong Python: Tạo số random ngẫu nhiên 
Lệnh cin và cout trong C++ 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Đệ quy đa tuyến (Exponential Recursion)
Trong bài này mình sẽ giới thiệu đến các bạn một trong các hàm đệ quy tiếp theo đó chính là đệ quy đa tuyến (Expenential Recursion).
Đây là một thuật toán được sử dụng khá nhiều trong các bài toán về sắp xếp.
Chúng ta sẽ cùng nhau tìm hiểu về đệ quy đa tuyến là gì? một vài ví dụ sử dụng đệ quy đa tuyến.
1. Đệ quy đa tuyến là gì?
Một hàm được gọi là đệ quy đa tuyến nếu mỗi lần gọi đệ quy nó phát sinh ra khoảng n lần gọi đệ quy khác. Thông thường câu lệnh gọi đệ quy được đặt trong các vòng lặp.
Bài viết này được đăng tại [free tuts .net]
Ví dụ chúng ta có một hàm đệ quy đa tuyến như sau:
void daTuyen(int i, int n, int *X)
{
int val;
for (val = 0; val < 2; val++)
{
X[i] = val;
if (i == (n-1))
{
int j;
for(j = 0; j < n; j ++)
{
cout<< X[j];
}
cout<<"\n";
}
else
{
daTuyen(i+1, n, X);
}
}
}Đây là một hàm tìm các dãy nhị phân có chiều dài n. Như các bạn thấy trong hàm có sử dụng vòng lặp và thực hiện gọi đệ quy ngay trong vòng lặp.
Cơ chế hoạt động của nó tương tự các hàm đệ quy khác, thay vào đó nó chỉ lặp đi lặp lại nhiều lần hơn mà thôi. Các bạn có thể thao khảo cơ chế hoạt động của các hàm đệ quy tại đây.
Bây giờ các bạn cùng mình tìm hiểu một vài ví dụ áp dụng hàm đệ quy đa tuyến để có thế hiểu rõ hơn về nó nhé.
2. Ví dụ 1 đệ quy đa tuyến
Ở ví dụ đầu tiên mình sẽ thực hiện bài toán tìm tất cả các dãy nhị phân có chiều dài n nhập từ bàn phím.
Hàm dayNhiPhan()
void dayNhiPhan(int i, int n, int *X)
{
int val; // val là các giá trị có thể gán cho các vị trí trong x
for (val = 0; val < 2; val++) // val có thể nhận hai giá trị là 0 và 1
{
X[i] = val;
if (i == (n-1)) // nếu i là phần tử cuối của dãy
{
int j;
for(j = 0; j < n; j ++) // thì tin ra nhị phân mới tìm được
{
cout<<X[j];
}
cout<<"\n";
}
else // nếu i chưa phải là phần tử cuối thì gán cho i sau là i+1.
{
dayNhiPhan(i+1, n, X); // gọi đệ quy tiếp tục thực hiện hàm
}
}
}Mình đã chú thích rất rõ ràng trong hàm, các bạn hãy đọc kỹ để hiểu rõ hơn nhé.
Full code:
#include<stdio.h>
#include<iostream>
using namespace std;
void dayNhiPhan(int i, int n, int *X)
{
int val; // val là các giá trị có thể gán cho các vị trí trong x
for (val = 0; val < 2; val++) // val có thể nhận hai giá trị là 0 và 1
{
X[i] = val;
if (i == (n-1)) // nếu i là phần tử cuối của dãy
{
int j;
for(j = 0; j < n; j ++) // thì tin ra nhị phân mới tìm được
{
cout<<X[j];
}
cout<<"\n";
}
else // nếu i chưa phải là phần tử cuối thì gán cho i sau là i+1.
{
dayNhiPhan(i+1, n, X); // gọi đệ quy tiếp tục thực hiện hàm
}
}
}
int main()
{
int n;
cout<<"Nhập n : ";
cin>>n;
int X[n];
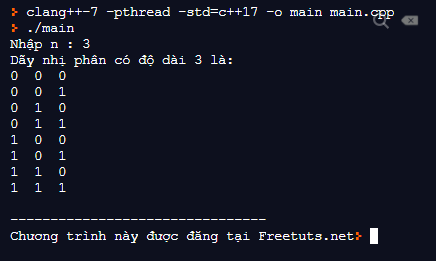
cout<<"Dãy nhị phân có độ dài "<<n<<" là:\n";
dayNhiPhan(0, n, X);
cout<<"\n--------------------------------\n";
cout<<"Chương trình này được đăng tại Freetuts.net";
}Kết quả:
3. Ví dụ 2 đệ quy đa tuyến
Trong ví dụ này mình sẽ thực hiện sắp xếp các số trong mảng M, sử dụng đệ quy đa tuyến để sắp xếp. Với các phần tử trong mảng M được nhập từ người dùng.
Hàm sort()
void sort(int arr[], int n, int i){
int j, swap;
//thực hiện vòng lặp để sắp xếp các phần tử
for(j = i + 1; j < n; j++){
if(arr[i] > arr[j]){ // Nếu phần tử trước lớn hơn phần tử sau thì thực hiện tráo đổi vị trí giữa hai phần tử
swap = arr[i];
arr[i] = arr[j];
arr[j] = swap;
}
sort(arr, n, i + 1);//Tiếp tục gọi đệ quy và thực hiện đến khi hàm kết thúc
}
}
Mình đã giải thích từng dòng lệnh trong hàm, các bạn có thể chạy tay hàm này để có thể hiểu được từng bước hoạt động của nó. Ở các bài trước mình đã biểu diễn cơ chế hoạt động một cách cụ thể thông qua Stack và cây.
Full code:
#include<stdio.h>
#include<iostream>
using namespace std;
/* hàm xuất các phần tử trong mảng */
void printArr(int arr[], int n){
for(int i = 0; i < n; i++) //chạy vòng lặp từng phần tử trong mảng
cout<<arr[i]<<"\t"; // xuất các phần tử trong mảng
cout<<endl;
}
/* hàm sắp xếp các phần tử trong mảng */
void sort(int arr[], int n, int i){
int j, swap;
//thực hiện vòng lặp để sắp xếp các phần tử
for(j = i + 1; j < n; j++){
if(arr[i] > arr[j]){ // Nếu phần tử trước lớn hơn phần tử sau thì thực hiện tráo đổi vị trí giữa hai phần tử
swap = arr[i];
arr[i] = arr[j];
arr[j] = swap;
}
sort(arr, n, i + 1);//Tiếp tục gọi đệ quy và thực hiện đến khi hàm kết thúc
}
}
int main()
{
int n;
int a[n];
do{
cout << "\nNhập vào số lượng phần tử có trong mảng: ";
cin >> n;
}while(n <= 0);
for(int i = 0;i < n;i++){
cout<<"a["<<i<<"]=";
cin >> a[i];
};
sort(a, n, 0);
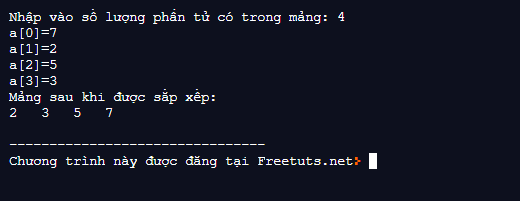
cout<<"Mảng sau khi được sắp xếp: \n";
printArr(a, n);
cout<<"\n--------------------------------\n";
cout<<"Chương trình này được đăng tại Freetuts.net";
}Kết quả:
Kết luận
Trên đây mình đã thực hiện hai ví dụ về việc sử dụng đệ quy đa tuyến. Các bạn hãy luyện tập bằng cách chạy tay các bài tập trên để nắm rõ các bước thực hiện của nó. Nếu các bạn thực hiện nhiều lần và thành thạo, điều đó giúp các bạn nhớ rất lâu và có một tư duy logic tốt.
