Lăng trụ tam giác đều, định nghĩa, tính chất và bài tập

Cùng tìm hiểu khái niệm, tính chất và các công thức tính diện tích, thể tích của một khối lăng trụ tam giác đều cùng các dạng bài tập liên quan.

Trong bộ môn hình học lớp 7, các em sẽ được tìm hiểu kiến thức liên quan về hình lăng trụ tam giác đều. Tuy nhiên, vì nội dung của bài học này rất nhiều nên chắc hẳn sẽ có nhiều bạn không thể tiếp thu hết được. Chính vì thế, trong bài viết hôm nay, freetuts sẽ đi sâu giảng giải và giúp các em hiểu rõ hơn về hình lăng trụ tam giác đều cũng như các bài tập liên quan. Cùng tìm hiểu ngay tại đây nhé!

Khái niệm Lăng trụ tam giác đều

Lăng trụ tam giác đều một lăng trụ đứng có hai đáy là hai tam giác đều.

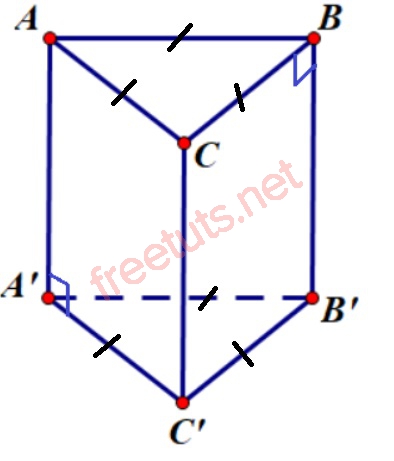
Hình lăng trụ đều ABC. A’B’C’

Tính chất Lăng trụ tam giác đều

Lăng trụ tam giác đều có đầy đủ tính chất của một lăng trụ đều, cụ thể như sau:

Bài viết này được đăng tại [free tuts .net]

• Trong lăng trụ tam giác đều, hai đáy là hai tam giác đều bằng nhau.
• Các mặt bên là các hình chữ nhật bằng nhau.
• Các cạnh bên luôn vuông góc với mặt đáy.

Ví dụ: Cho lăng trụ tam giác đều ABC.A’B’C’, ta có:

• Tam giác đều ABC = tam giác đều A’B’C’.
• ABA’B, BCB’C’, ACA’C’ là hình chữ nhật.
• AA’ vuông góc với ABC và A’B’C’, BB’ vuông góc với ABC và A’B’C’, CC’ vuông góc với ABC và A’B’C’.

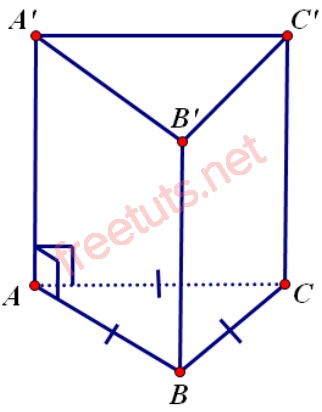
Mặt phẳng đối xứng trong lăng trụ tam giác đều

Mặt phẳng đối xứng của lăng trụ tam giác đều là mặt phẳng mà chia hình lăng trụ tam giác đều thành 2 phần đối xứng với nhau. Mỗi lăng trụ tam giác đều có 4 mặt phẳng đối xứng lần lượt là:

• 1 mặt phẳng đi qua trung điểm của các cạnh bên.
• 3 mặt phẳng lần lượt chứa các đường phân giác của các cặp góc ở đỉnh của tam giác đều.

Ví dụ:

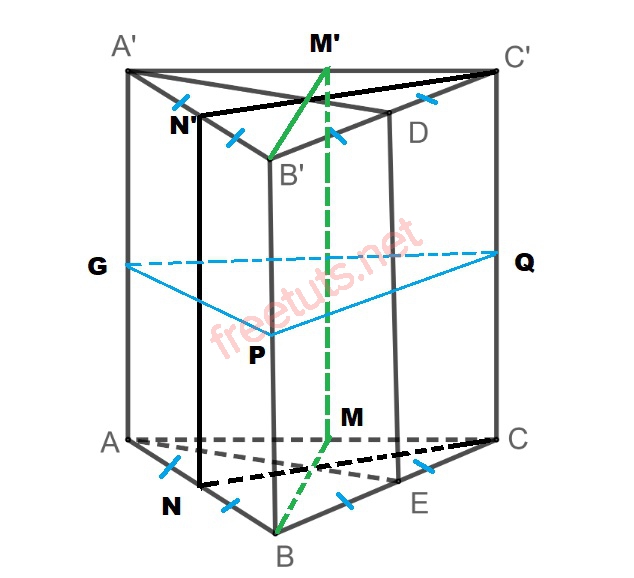
Cho hình lăng trụ tam giác đều ABC.A’B’C như hình vẽ trên. Lúc này ta có các mặt phẳng AA’DE, CC’N’N, BB’M’M và GPQ là 4 mặt phẳng đối xứng của lăng trụ tam giác đều.

Công thức tính diện tích, thể tích lăng trụ tam giác đều

Cùng tìm hiểu về công thức tính diện tích xung quanh, diện tích toàn phần và thể tích lăng trụ tam giác đều ngay bên dưới đây nhé.

Công thức tính diện tích xung quanh lăng trụ tam giác đều

Diện tích xung quanh của hình lăng trụ tam giác đều (Sxq) bằng chu vi đáy nhân với chiều cao.

Công thức: Sxq = P x h.

Trong đó:

• P là chu vi đáy.
• h là chiều cao

Ví dụ minh họa:

Cho hình lăng trụ tam giác đều MNP.M’N’P’ có độ dài cạnh đáy MN = 4 cm, chiều cao MM’ = 6cm, tính Sxq(MNP.M’N’P’)

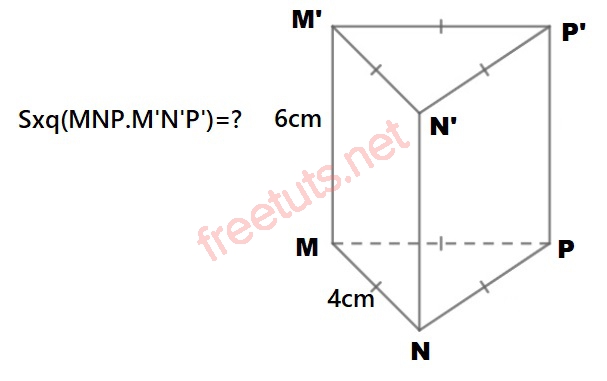
Hướng dẫn giải:

Chu vi tam giác đều MNP là:

P(MNP) = 3 x MN = 3 x 4 = 12 (cm)

Công thức tính diện tích xung quanh của hình lăng trụ đứng tam giác đều MNP.M’N’P’ là:

Sxq (MNP.M’N’P’) = P(MNP) x MM’ = 12 x 6 = 72 cm2

Đáp số: 72 cm2.

Công thức tính diện tích toàn phần lăng trụ tam giác đều

Diện tích toàn phần của hình lăng trụ tam giác đều (Stp) bằng tổng diện tích xung quanh và diện tích 2 mặt đáy.

Công thức: Stp = Sxq + 2Sđáy

Ví dụ minh họa:

Cho lăng trụ tam giác đều ABC.A’B’C’ có độ dày cạnh đáy AB = 3cm, chiều cao AA’ = 5cm, tính diện tích toàn phần của lăng trụ ABC.A’B’C’.

Hướng dẫn giải:

Chu vi tam giác đều ABC là:

P(ABC) = 3 x AB = 3 x 3 = 9 (cm)

Diện tích xung quanh của lăng trụ đều ABC.A’B’C’ là:

Sxq = P(ABC) x AA’ = 9 x 5 = 45 (cm)

Diện tích hai đáy của lăng trụ đều ABC.A’B’C’ là:

S2 đáy = 2 x S(ABC) = 2 x S(A’B’C’) = 2 x ½ x AB x AB x√3/2 = 2 x ½ x 9 x√3/2 = 9√3/2 (cm2)

Diện tích toàn phần lăng trụ tam giác đều ABC.A’B’C’ là:

Stp = Sxq + 2Sđáy = 45 + 9√3/2 = 52,79 (cm2)

Đáp số: 52,79 cm2

Công thức tính thể tích của hình lăng trụ tam giác đều

Thể tích của hình lăng trụ tam giác đều bằng diện tích đáy nhân với chiều cao.

Công thức: V = Sđáy x h

Trong đó:

• Sđáy là diện tích mặt đáy của lăng trụ tam giác đều.
• h là chiều cao.

Ví dụ minh họa:

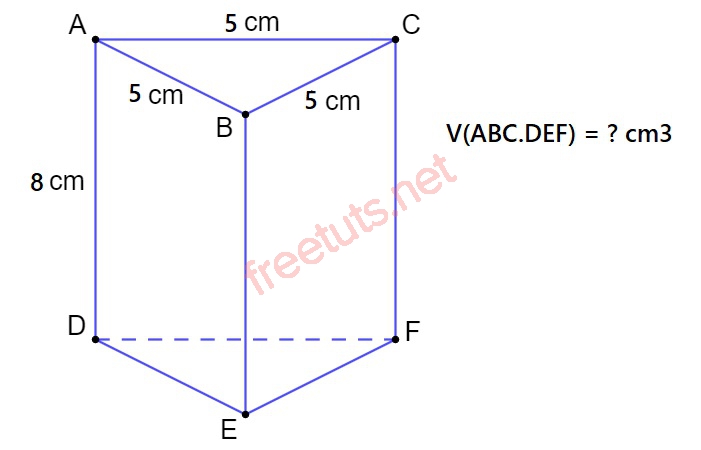
Cho hình lăng trụ tam giác đều ABC.DEF có độ dài cạnh đáy là 5cm, chiều cao là 8 (cm), tính thể tích ABC.DEF

Hướng dẫn giải:

Diện tích đáy của tam giác đều ABC là:

Sđáy = S(ABC) = S(DEF) = ½ x AB x AB√3/2 = ½ x 25 x√3/2 = 25√3/4 (cm2)

Thể tích của lăng trụ đều ABC.DEF là:

V = Sđáy x h = 25√3/4 x 8 = 422 (cm3)

Đáp số: 422 (cm3)

Bài tập về Lăng trụ tam giác đều

Cùng freetuts tìm hiểu một số dạng bài tập liên quan đến lăng trụ tam giác đều ngay bên dưới đây nhé!

Dạng 1: Tính diện tích xung quanh lăng trụ tam giác đều

Bài tập 1:

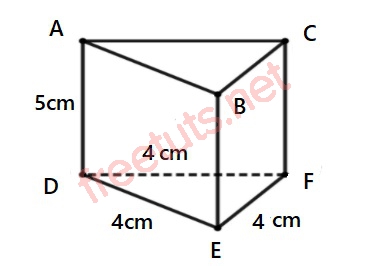
Cho hình lăng trụ đứng tam giác đều ABC.DEF có độ dài AD = 5cm, DE = EF = DF = 4cm, tính diện tích toàn phần của ABC.DEF.

Hướng dẫn giải:

Diện tích xung quanh của lăng trụ đứng tam giác đều ABC.DEF là:

S(ABC.DEF) = (DE + DF + EF) x AD = (4 + 4 + 4) x 5 = 60 cm2.

Đáp án: 60 cm2.

Bài tập 2: Cho hình lăng trụ đứng tam giá đều ABC.A’B’C’ có độ dài cạnh đáy = 5cm, diện tích xung quanh = 80 cm2, tính chiều cao AA’ =?cm.

Hướng dẫn giải:

Áp dụng công thức tính diện tích xung quanh của lăng trụ đứng tam giác đều ta có:

Sxq = Pđáy x chiều cao ⟹ Chiều cao = Sxq / P đáy.

Vậy chiều cao AA’ = Sxq/ P(DEF) = 80/(5+5+5) = 5,3 cm.

Đáp án: AA’ = 5,3cm.

Dạng 2: Tính diện tích toàn phần hình lăng trụ tam giác đều

Bài tập: Cho lăng trụ tam giác đều ABC.DEF có độ dày cạnh đáy DE = 4cm, chiều cao AD = 6cm, tính diện tích toàn phần của lăng trụ ABC.DEF.

Hướng dẫn giải:

Chu vi tam giác đều DEF là:

P(DEF) = 3 x DE = 3 x 4 = 12 (cm)

Diện tích xung quanh của lăng trụ đều ABC.DEF là:

Sxq = P(DEF) x AD = 12 x 6 = 72 (cm)

Diện tích hai đáy của lăng trụ đều ABC.DEF là:

S2 đáy = 2 x S(ABC) = 2 x S(DEF) = 2 x ½ x DE x DE x√3/2 = 2 x ½ x 16 x√3/2 =8√3 (cm2)

Diện tích toàn phần lăng trụ tam giác đều ABC.A’B’C’ là:

Stp = Sxq + 2Sđáy = 72 + 8√3 = 85,85 (cm2)

Đáp số: 85,85 cm2

Dạng 3: Tính thể tích hình lăng trụ tam giác đều

Bài tập:

Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a, hãy tính thể tích khối lăng trụ tam giác đều cạnh a đó.

Hướng dẫn giải:

Diện tích của tam giác đều ABC là:

S(ABC) = ½ AB x chiều cao tam giác ABC = ½ x a x a√3/2 = a^2√3/4.

Thể tích khối lăng trụ tam giác đều có các cạnh bằng a là:

V = Sđáy x h = a x a^2√3/4 = a^3√3/4.

Đáp số: a^3√3/4

Dạng 4: Bài tập trắc nghiệm lăng trụ tam giác đều

Câu 1: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?

A. 1 mặt phẳng

B. 2 mặt phẳng

C. 3 mặt phẳng

D. 4 mặt phẳng.

Đáp án D là đáp án đúng. Một lăng trụ tam giác đều sẽ có 4 mặt phẳng đối xứng.

Câu 2: Thể tích của một khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a sẽ là?

A. a^3√2/3

B. a^3√2/6

C. a^3√2/2

D. a^3√2/4

Đáp án đúng là C.

Câu 3: Một lăng trụ tam giác đều có tất cả bao nhiêu mặt?

A. 5 mặt gồm 3 mặt bên, 2 mặt đáy.

B. 4 mặt gồm 2 mặt bên, 2 mặt đáy.

C. 5 mặt gồm 2 mặt bên, 3 mặt đáy.

D. 6 mặt gồm 3 mặt bên, 3 mặt đáy.

Đáp án đúng là A. 5 mặt gồm 3 mặt bên và 2 mặt đáy.

Câu 4: Hình Lăng trụ tam giác đều có đứng không?

A. Có.

B. Không

Đáp án đúng A. Có

Vì theo định nghĩa ta có lăng trụ tam giác đều là một lăng trụ ĐỨNG có đáy là tam giác đều.

Câu 5: Hình lăng trụ đều có đáy là tam giác gì?

A. Tam giác vuông cân.

B. Tam giác cân.

C. Tam giác đều.

D. Tam giác bất kỳ.

Đáp án đúng là C. Tam giác đều

Câu 6: Lăng trụ tam giác đều có các mặt bên là hình gì?

A. Hình tam giác.

B. Hình chữ nhật

C. Hình tròn

Đáp án đúng là B. Hình chữ nhật.

Dạng 5: Bài tập nâng cao

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều ABC, biết (ABC’) tạo với mặt phẳng đáy góc 60 độ, diện tích ABC’ = √3a^2, tính thể tích ABC.A’B’C’

Hướng dẫn giải:

Gọi M là trung điểm của cạnh đáy AB, vì ABC là tam giác đều nên ta có CM vuông góc với AB. Tương tự ta có C’M cũng vuông góc với AB.

Theo đề bài, ta có góc CMC’ = 60 độ.

Xét tam giác MCC’ vuông tại C, ta có:

MC’ = MC/(Cos60) = BC x sin B x ½ = 2AB. Sin 60 = √3AB (1)

Theo đề bài, ta có diện tích tam giác ABC’ = √3a^2, ta có:

S(ABC) = ½ MC’.AB = √3a^2 ⇔ MC’.AB = 2√3a^2 (2)

Từ (1) và (2) ta có:

√3AB.AB = 2√3a^2 ⇔AB.AB = 2a^2

⟹ AB = √2a ⟹ MC = a√6

Diện tích tam giác ABC là:

S (ABC) = ½ CM x AB = ½ AB sin 60 x AB = √3a^2/2

Thể tích khối lăng trụ tam giác đều ABC.A’B’C’ là:

V(ABC.A’B’C’) = S(ABC).CC’ = 3√6/4a^3

Đáp số: 3√6/4a^3

Bài viết trên đã chia sẻ khái niệm, tính chất của một lăng trụ tam giác đều đi kèm những công thức tính diện tích xung quanh, diện tích toàn phần hay thể tích của hình lăng trụ này và một số bài tập có liên quan. Hy vọng đây sẽ là những kiến thức bổ ích cho các em học sinh lớp 7.

Nếu các em muốn tìm hiểu thêm các kiến thức môn toán khác hãy ghé ngay chuyên mục Toán học của freetuts.net ngay nha, còn rất nhiều bài học hữu ích chờ các em khám phá đó nè.