Cách viết phương trình tiếp tuyến của đường tròn và bài tập

Cách viết phương trình tiếp tuyến của đường tròn khi biết tọa đọa một điểm thuộc đường tròn, khi biết tiếp tuyến song song hoặc vuông góc với một đường thẳng cho trước.

Phương trình tiếp tuyến của đường tròn là một bài học vô cùng quan trọng trong chương trình toán lớp 10, tuy nhiên, hiện nay, có nhiều em học sinh chưa nắm rõ được cách viết phương trình tiếp tuyến của một đường tròn bất kỳ.

Chính vì thế, trong bài viết hôm nay, freetuts sẽ giúp các em ôn lại phần lý thuyết quan trọng này và hướng dẫn chi tiết cách viết pt tiếp tuyến của đường tròn nhé.

Lý thuyết hương trình tiếp tuyến của đường tròn

Phương trình tiếp tuyến đường tròn là gì?

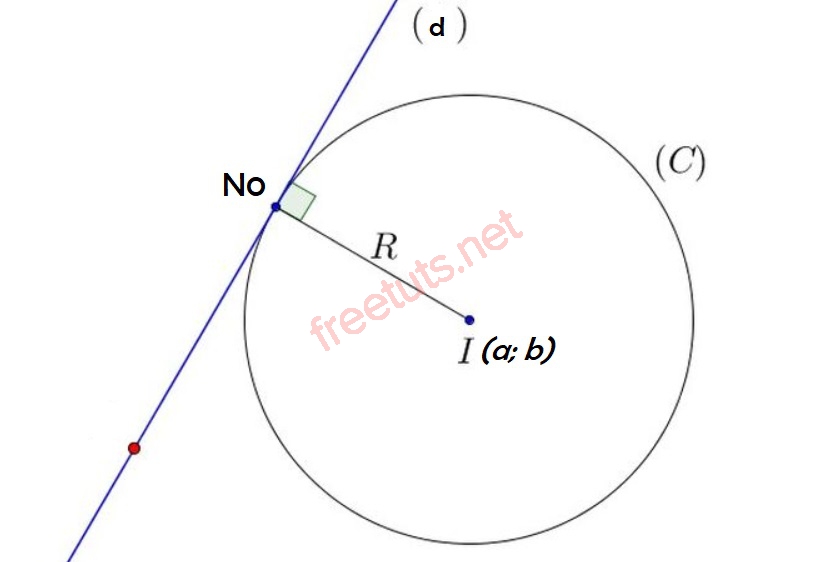
Đường thẳng d tiếp tuyến với đường tròn (C) tại N0.

PT tiếp tuyến của đường tròn là một phương trình tuyến tính biểu diễn cho một đường thẳng bất kỳ tiếp xúc với đường tròn tại điểm nhất định thuộc đường tròn đó.

Bài viết này được đăng tại [free tuts .net]

Cho điểm N0(x0; y0) thuộc đường tròn (C) (x - a)^2 + (y - b)^2 = 0 , tâm I(a; b), gọi d là tiếp tuyến của © tại N0, lúc này, ta có:

N0 thuộc d và véc tơ IN0 = (x0 - a; y0 - b) là véc tơ pháp tuyến của đường thẳng d.

Vậy, công thức phương trình tiếp tuyến d là:

(x0 - a).(x - x0) + (y0 - b).(y - y0) = 0 (1)

Lúc này, ta gọi (1) là pt tiếp tuyến của đường tròn (C) (x - a)^2 + (y - b)^2 = 0 tại điểm N0(x0; y0).

Một đường tròn có thể có bao nhiêu phương trình tiếp tuyến?

Đối với một đường tròn bất kỳ, chúng ta có thể lập nhiều phương trình tiếp tuyến khác nhau phụ thuộc vào điểm tiếp tuyến trên đường tròn và hướng của tiếp tuyến, chính vì vậy, số lượng pt tiếp tuyến sẽ phụ thuộc vào dữ liệu của bài toán đưa ra.

Cách viết phương trình tiếp tuyến của đường tròn

Có rất nhiều cách để viết được pt tuyến tuyến đường tròn bất kỳ, mời các em cùng tham khảo một số trường hợp mà freetuts đã tổng hợp ngay dưới đây nha.

Khi biết tọa độ một điểm thuộc đường tròn

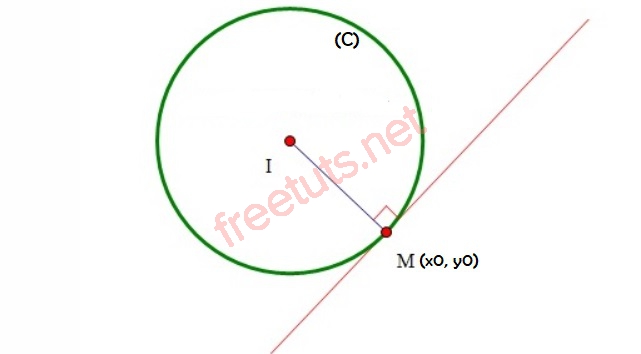
Phương trình tiếp tuyến đi qua điểm M, thuộc đường tròn (C).

• Dạng 1: Cho đường tròn (C) có pt: x^2 + y^2 + 2ax + 2by + c = 0, điểm M(x0, y0) thuộc (C).

Ta có, phương trình tiếp tuyến tại M(x0, y0) của (C) là:

x0x + y0y + a(x0 + x ) + b(y0 + y) + c = 0.

• Dạng 2: Cho đường tròn (C) có pt: (x - a)^2 + (y - b)^2 = R^2, điểm M(x0, y0) thuộc (C).

Ta có, pt tiếp tuyến tại M(x0, y0) là:

(x0 - a)(x - a) + (y0 - b)(y - b) = R^2.

Ví dụ minh họa:

Cho đường tròn (C) có phương trình x^2 + y^2 + 6x + 6y - 20 = 0, điểm M(2; 1) thuộc (C), viết phương trình tiếp tuyến với đường tròn C tại M.

Lời giải:

Với M(2; 1) thuộc (C), vậy phương trình tiếp tuyến của C tại M là:

2.x + 1.y + 3(2 + x) + 3(1+ y) - 20 = 0

2x + y + 6 + 3x + 3 + 3y - 20 = 0

5x + 4y -11 = 0.

Khi biết tọa độ của tâm và đi qua một điểm cho trước

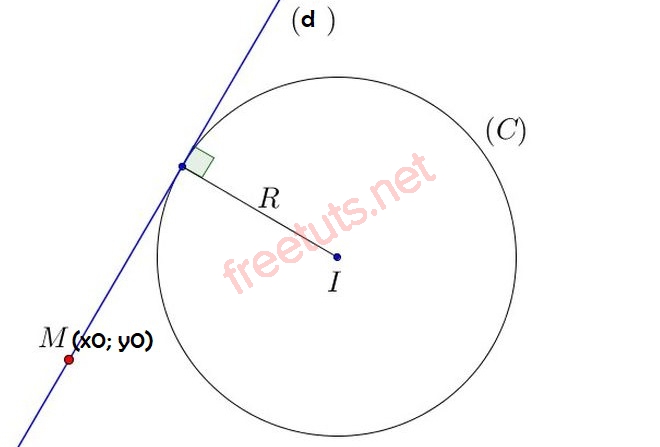
PT tiếp tuyến d đi qua M(x0, y0).

Cho đường tròn (C) có pt: (x - a)^2 + (y - b)^2 = R^2, điểm M(x0, y0) là điểm tiếp tuyến của đường tròn, hãy lập pt tiếp tuyến (d) của (C).

• Bước 1: Dựa vào phương trình đường tròn, suy ra tâm và bán kính.

Xét (C) có pt: (x - a)^2 + (y - b)^2 = R^2, suy ra đường tròn C có tâm I(a; b) và bán kính R.

• Bước 2: Lập pt tiếp tuyến (d) tại M.

Do đường thẳng d là tiếp tuyến của đường tròn tại điểm M, nên suy ra d sẽ vuông góc với IM, vậy đường thẳng d sẽ đi qua điểm M và có véc tơ pháp tuyến là IM.

Ví dụ minh họa:

Cho đường tròn (C) : (x - 1)^2 + (y + 2)^2 = 2. Viết phương trình tiếp tuyến d của đường tròn C tại điểm M(3; -4).

Lời giải:

Xét pt đường tròn (C) : (x - 1)^2 + (y + 2)^2 = 2, ta có tâm I(1; -2), bán kính R = căn bậc 2 của 2.

Vì d tiếp xúc với C tại M(3 ; -4), nên d sẽ vuông góc với IM, véc tơ pháp tuyến IM(2; -2)

Phương trình tiếp tuyến của đường tròn là (d): 2(x -3) - 2(y + 4) = 0 (d): x - y = 7.

Khi biết tiếp tuyến song song với đường thẳng cho trước

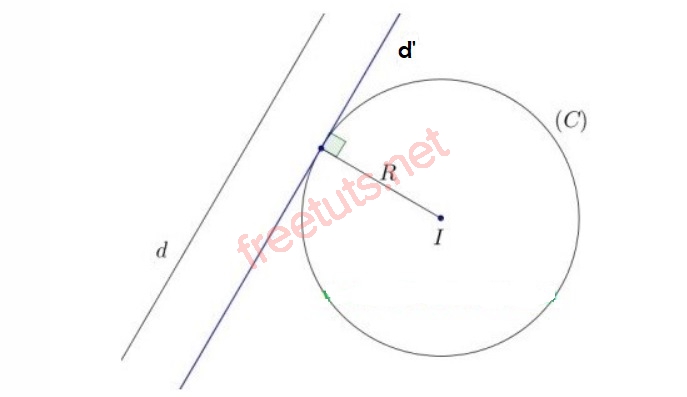
Đường thẳng d’ là pt tiếp tuyến của (C) và song song với d.

Cho đường tròn (C) có pt: (x - a)^2 + (y - b)^2 = R^2, đường thẳng (d): Ax + By + C = 0. Viết phương trình tiếp tuyến () của (C) , biết () song song với (d).

• Bước 1: Dựa vào pt đường tròn, xác định tâm I và bán kính R của đường tròn.
• Bước 2: Viết pt tiếp tuyến.
  • Vì () song song với (d) nên (): Ax + By + c =0 (1), với c khác 0,
  • Do () tiếp xúc với đường tròn (C ), nên d(I, ()) = R (2).
  • Giải phương trình (1) và (2), ta sẽ tìm được c và suy ra được pt tiếp tuyến của đường tròn C.

Ví dụ minh họa:

Cho đường tròn (C) có pt: (x - 1)^2 + (y + 3)^2 = 16, đường thẳng (d): 6x - 8y + 2023 =0, hãy viết pt tiếp tuyến (d’) của C, biết (d’) song song với (d).

Lời giải:

Xét (C) có pt: (x - 1)^2 + (y + 3)^2 = 16, ta có đường tròn có tâm I(1; -3), bán kính R = 4.

Vì d’ // d, nên d’: 6x - 8y + c = 0, c khác 2023.

d’ tiếp xúc với (C ) d(I, d’) = R |30 + c|100 = 4 c = 10 hoặc c = -70.

Vậy có 2 phương trình tiếp tuyến của đường tròn, song song với d là:

d’1 = 6x - 8y + 10 = 0 và d’2 = 6x - 8y -10 = 0.

Khi biết tiếp tuyến vuông góc với đường thẳng cho trước

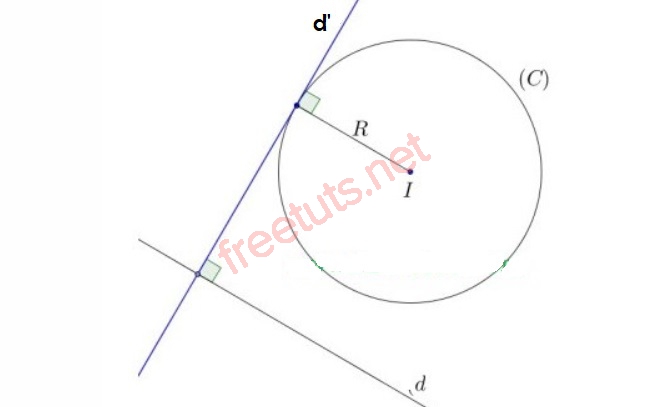
Hình minh họa phương trình tiếp tuyến d’ vuông góc với d.

Cho đường tròn (C) có pt: (x - a)^2 + (y - b)^2 = R^2, đường thẳng (d): Ax + By + C = 0, viết phương trình tiếp tuyến d’ của C, biết d’ vuông góc với d.

• Bước 1: Dựa vào pt đường tròn, xác định tâm I và bán kính R của đường tròn.
• Bước 2: Do d’ vuông góc với d nên d’ có dạng: Bx - Ay + c = 0.

d’ tiếp xúc với (C) nên d(I, d’) = R, giải phương trình tìm được c.

Ví dụ minh họa:

Cho đường tròn (C): x^2 + y^2 - 4x + 8y - 5 = 0, đường thẳng (d): 3x + 4y + 2023 =0.

Viết phương trình tiếp tuyến d’ của đường tròn C biết d’ vuông góc với d.

Lời giải:

Xét pt (C): x^2 + y^2 - 4x + 8y - 5 = 0, ta có tâm I(2; -4 ), bán kính R = 5.

Vì d’ vuông góc với d, nên d’ có dạng: 4x - 3y + c = 0.

d’ tiếp xúc với C, nên d(I, d’) = R |20 + c|/25 = 5 c = 5, hoặc c = -45.

Vậy có 2 phương trình tiếp tuyến là:

d’1: 4x - 3y + 5 = 0, và d’2 : 4x - 3y -45 = 0

Bài tập viết phương trình tiếp tuyến của đường tròn và cách giải

Sau khi đã nắm vững lý thuyết và các cách viết pt tiếp tuyến của đường tròn, các em hãy vận dụng để giải một số bài tập sau nha:

Bài 1: Cho đường tròn (C): (x + 3)^2 + (y + 1)^2 = 1, điểm M(-4; 1), Viết phương trình tiếp tuyến của (C) tại điểm M.

Lời giải:

Với đường tròn (C): (x + 3)^2 + (y + 1)^2 = 1, ta có tâm I(-3; -1), bán kính R = 1.

Gọi d là tiếp tuyến của C, đi qua điểm M(-4, 1), lúc này d có dạng:

A (x + 4) + B(y - 1) = 0 (Ax + By + 4A - B = 0, với A^2 + B^2 khác 0

Vì d tiếp xúc với C, nên d (I, d) = R |A - 2B|/A2+B2=1 -4AB + 3B^2 = 0

B = 0 -4A + 3B = 0.

• Với B = 0, chọn A = 1, ta có pt tiếp tuyến d là x + 4 = 0.
• Với -A4 + 3B = 0, chọn A = 3, B = 4, ta có pt tiếp tuyến d là 3x + 4y + 8 = 0

Vậy có 2 pt tiếp tuyến với đường tròn C, đi qua M(-4; 1) là x + 4 = 0 và 3x + 4y + 8 = 0.

Bài 2: Cho đường tròn (C): (x - 4)^2 + (y + 1)^2 = 9, đường thẳng d: 2x + y + 5 = 0, viết pt tiếp tuyến d’ của (C), biết d’ song song với d.

Lời giải:

Vì d’ song song với d nên d’ có dạng: 2x + y + m = 0, với m khác 5.

Đường tròn (C): (x - 4)^2 + (y + 1)^2 = 9, suy ra tâm I(4; -1), R = 9.

Đường thẳng d’ tiếp xúc với C, khi:

d(I, d’) = R |2.4 - 1 + m|.9 = 9 |7+m| =1 7+m = 1 hoặc 7 + m = -1

m = -6 hoặc m = -8.

Vậy d’ = 2x + y - 6 = 0, hoặc d’1 = 2x + y - 8 = 0.

Bài tập tự luyện viết phương trình tiếp tuyến của đường tròn

Sau đây là một số bài tập để các em có thể tự ôn luyện lại phần kiến thức quan trọng này nha:

• Câu 1: Viết pt tiếp tuyến d của đường tròn (C): (x + 3)^2 + (y + 4)^2 = 25 tại điểm M(2,1).
• Câu 2: Viết pt tiếp tuyến của đường tròn (C): (x - 4)^2 + (y + 1)^2 = 5, biết tiếp tuyến này song song với đường thẳng d: 3x + y + 7 = 0.
• Câu 3: Cho đường tròn (C): (x - 3)^2 + (y + 2)^2 = 2. Viết phương trình tiếp tuyến d của (C), biết d đi qua điểm N(4;0).

Như vậy, qua bài viết trên, freetuts.net đã tổng hợp các cách viết phương trình tiếp tuyến của đường tròn trong các trường hợp đặc biệt, hy vọng các em học sinh có thể áp dụng những kiến thức này một cách thuần thục để có thể đạt kết quả cao trong học tập.