Tổng hợp các tác giả văn học hiện đại Việt Nam 
Số tự nhiên là gì? Sự khác nhau giữa tập hợp N và N* 
Tiểu sử nhà văn Tô Hoài: Sự nghiệp sáng tác văn học của ông 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Cách tính chu vi hình thang và bài tập thực hành
Bài viết này sẽ đăng công thức tính chu vi hình thang, bên cạnh đó kèm theo các bài tập thực hành.
Chu vi hình thang là một kiến thức cơ bản trong bộ môn hình học. Hi vọng bài viết dưới đây sẽ giúp ích cho các bạn trong việc thực hiện các bài tập một cách đơn giản và nhanh chóng.
1. Chu vi hình thang là gì?
Chu vi hình thang là tổng độ dài các cạnh của hình thang đó. Nó chính là độ dài củ các đường biên tạo nên hình thang.
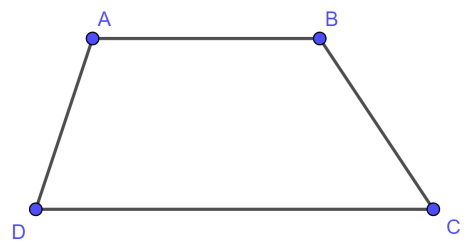
Theo như trong hình thì chu vi sẽ bằng các cạnh: AB + BC + CD + DA.
Bài viết này được đăng tại [free tuts .net]
2. Cách tính chu vi hình thang
Dựa vào khái niệm của chu vi hình thang chúng ta rút ra được cách tính chu vi của một hình thang đó là: Chu vi hình thang sẽ bằng tổng số đo độ dài của hai đáy và hai cạnh bên của hình thang.
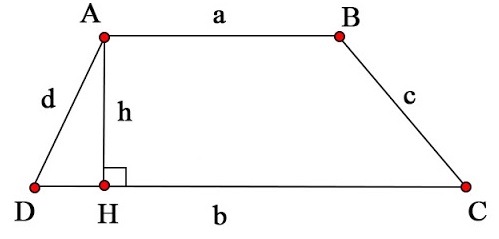
Cho hình thang và các ký hiệu như sau:
Công thức tổng quát: (! P = a + b + c + d !)
Trong đó:
- P là kí hiệu của chu vi
- a,b là hai cạnh đáy của hình thang
- c,d là hai cạnh bên của hình thang
Ví dụ: Cho hình thang có độ dài hai cạnh đáy và hai cạnh bên lần lượt là 8cm,9cm,6cm và 7cm. Tính chu vi của hình thang đó?
Dựa vào công thức tính chu vi ta có chu vi của hình thang đó là: (! P = 8+9+6+7 = 30(cm) !)
Đáp số: 30(cm)
Đối với hình thang vuông chúng ta cũng sẽ có cách tính chu vi tương tự như cách tính chu vi của hình thang thường.
Nhưng đối với hình thang cân chúng ta sẽ có cách tính khác hơn một chút, chúng ta cùng tiếp tục tìm hiểu nhé.
3. Cách tính chu vi hình thang cân
Vì hình thang cân là hình có hai góc kề một đáy bằng nhau và hai cạnh bên bằng nhau nên chúng ta có công thức tính chu vi hình thang cân như sau:
(!! P= (2 \times a) + b + c !!)
Ví dụ: Cho hình thang có hai cạnh đáy lần lượt là 6cm và 4cm. Chiều dài của cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó?
Gọi a là chiều dài của cạnh bên hình thang, nó được có giá trị là: (! a = (6+4) \times 2 = 5(cm) !)
Áp dụng công thức, ta có chu vi của hình thang đó là: (! P = (2 \times 5) + 6 + 4 = 20(cm) !)
Đáp số: 20 cm
Hi vọng bài viết trên sẽ giúp các bạn nắm bắt và củng cố lại kiến thức cơ bản về cách tính chu vi hình thang. Chúc các bạn học tập tốt.
