Công thức tính khoảng cách đầy đủ và bài tập áp dụng

Tổng hợp công thức tính khoảng cách giữa hai điểm, từ điểm tới đường thẳng, khoảng cách từ điểm tới mặt phẳng, khoảng cách giữa 2 mặt phẳng trong không gian,...

Trong chương trình toán THPT, công thức tính khoảng cách là một phần kiến thức hết sức cơ bản mà bất kỳ em học sinh nào cũng cần phải nắm vững để làm nền tảng giải các bài toán chuyên sâu hơn. Trong bài viết hôm nay, hãy cùng freetuts ôn tập lại các công thức liên quan đến tính khoảng cách quan trọng nha.

Công thức tính khoảng cách giữa hai điểm

Trong mặt phẳng Oxy

Cho hệ trục tọa độ phẳng Oxy, điểm M(a,b), điểm N (,), lúc này, khoảng cách giữa hai điểm MN sẽ được tính bằng công thức sau:

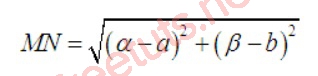
Ví dụ minh họa:

Bài viết này được đăng tại [free tuts .net]

Trong mặt phẳng Oxy, cho hai điểm M(2; 3), điểm N(4,1), hãy tính tính khoảng cách giữa 2 điểm tọa độ M và N.

Lời giải:

Áp dụng ct tính khoảng cách hai điểm, ta có:

MN = (4-2)2+(1-3)2=8

Trong mặt phẳng Oxyz ( Trong không gian 3 chiều)

Trong không gian, cho hệ trục tọa độ Oxyz, và 2 điểm M(a, b, c) và điểm N(; ; ), lúc này, ta có khoảng cách giữa hai điểm MN sẽ được tính như sau:

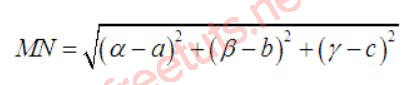
Ví dụ minh họa:

Trong không gian Oxyz, cho điểm M(2,3,4), N(3,2,3), tính khoảng cách MN = ?

Lời giải:

Áp dụng ct tính khoảng cách 2 điểm trong không gian, ta có:

MN = (2-3)2 + (3-2)2 + (4-3)2=3

Công thức tính khoảng cách từ điểm đến đường thẳng

Trong hệ trục tọa độ Oxy, cho đường thẳng d: ax + by + c = 0, điểm M (x0,y0), lúc này khoảng cách từ điểm M đến đường thẳng d được tính theo công thức:

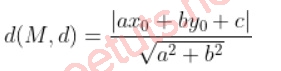
Ví dụ minh họa: Cho đường thẳng d : 3x + 2y - 2 = 0, điểm M(1; 2), tính khoảng cách từ M đến đường thẳng d.

Lời giải:

Áp dụng ct tính khoảng cách từ một điểm đến đường thẳng, ta có:

d(M,D) = |3.1 + 2.2 - 2|/32+22=5/12

Công thức tính khoảng cách từ điểm đến mặt phẳng Oxyz

Khoảng cách từ một điểm tới mặt phẳng là khoảng cách được tính từ điểm đó tới hình chiếu vuông góc của nó trên mặt phẳng đó.

Trong hệ trục Oxyz, cho A(, , ), mặt phẳng (P): ax + by + cz + d = 0. Khoảng cách từ điểm A tới mặt phẳng P được tính theo công thức như sau:

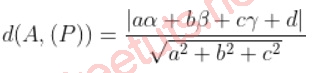
Ví dụ minh họa:

Cho mặt phẳng (P) 3x + 2y + 4z - 2 = 0, điểm M(1,2,-3), tính khoảng cách từ điểm M tới mặt phẳng P.

Lời giải:

Áp dụng ct, ta có:

d(M, (P)) = |3.1 + 2.2 + 4.-3 -2|/32+22 + 42 = 7/29

Công thức tính khoảng cách giữa 2 đường thẳng chéo nhau, song song.

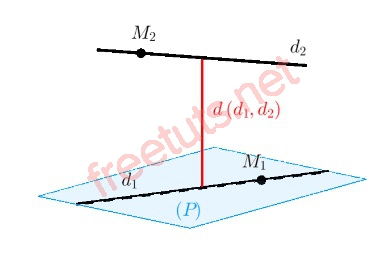
Khoảng cách giữa hai đường thẳng chéo nhau.

Khoảng cách giữa 2 đường thẳng chéo nhau hoặc song song, được tính bằng khoảng cách từ một điểm trên đường thẳng này đến đường thẳng kia.

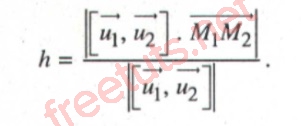
Cho 2 đường thẳng d1 và d2, d1 đi qua điểm M1, có véc tơ chỉ phương u1, d2 đi qua điểm M2, có vecto chỉ phương u2, lúc này, ta có ct tính khoảng cách giữa hai đường thẳng d1 và d2 là:

Ví dụ minh họa:

Cho 2 đường thẳng d1 và d2 có phương trình như sau:

d1: = x/1 = (y - 1)/2 = (z - 6)/3 và (d2): x = 1 + t, y = -2 + t, z = 3 - t.

Tình khoảng cách giữa d1 và d2.

Lời giải:

d1: = x/1 = (y - 1)/2 = (z - 6)/3, vậy d1 đi qua điểm M1(0; 1; 6), có véc tơ chỉ phương u1 = (1; 2; 3).

(d2): x = 1 + t, y = -2 + t, z = 3 - t, vậy d2 đi qua điểm M2(1; -2; 3) và có véc tơ chỉ phương u2 = (1; 1; -1).

M1M2= (1; -3; -3), [u1.u1] = (-5; 4; -1), vậy [u1.u1] .M1M2= -14

Khoảng cách giữa d1 và d2 là:

d = |[u1.u1] .M1M2|/|[u1.u1]| = 14/25+16+1= 42/3.

Công thức tính khoảng cách giữa 2 mặt phẳng trong không gian

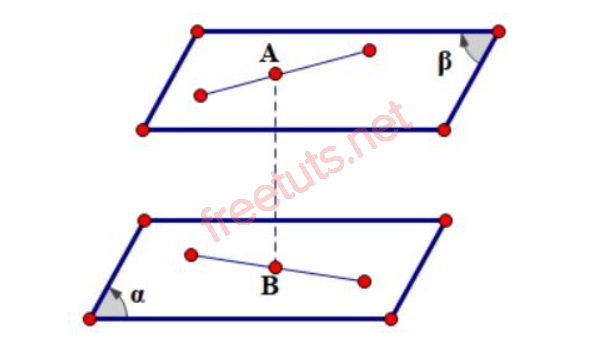
Cho hai mặt phẳng (P), (Q) song song, (P): ax + by + cz + d = 0, (Q) = ax + by + cz + d’ = 0,

với (a^2 + b^2 + c^2 > 0, d khác d’.

Cho điểm M ( ; ; ) thuộc (P), a. + b. + c. = -d, vậy khoảng cách giữa (P) và (Q), chính bằng khoảng cách giữa M và (Q), ta có các công thức tính khoảng cách lớp 12 về hai mặt phẳng trong không gian như sau:

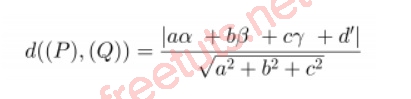
Hoặc:

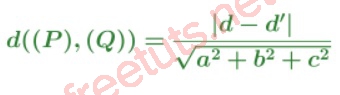
Ví dụ minh họa:

Cho mặt phẳng (P): x + 2y + 2z + 4 = 0, (Q) 2x + 4y + 4z - 10 = 0, tính khoảng cách giữa (P) và (Q).

Lời giải:

Với (Q) 2x + 4y + 4z - 10 = 0 x + 2y + 2z - 10 = 0

d((P),(Q)) = |4 -(- 5)|/12+22+22 = 11/9

Vậy, khoảng cách giữa hai mặt phẳng (P) và (Q) là 11/9.

Công thức tính khoảng cách 2 điểm cực trị

Trong toán học, không có một công thức chung nào để tính được khoảng cách giữa hai điểm cực trị nếu chưa biết được thông tin cụ thể về các hàm số. Vì vậy, muốn tính được khoảng cách giữa 2 điểm cực trị, có thể chia làm các trường hợp sau:

• Trường hợp 1: Nếu hàm số đang xét là hàm bậc nhất hoặc bậc 2, hãy áp dụng pt đường thẳng hoặc đường cong để tính khoảng cách giữa hai điểm.
• Trường hợp 2: Nếu hàm số đang xét là hàm bậc 3, 4 hoặc phức tạp hơn, các em hãy sử dụng tích phân, đạo hàm để giải các phương trình này nhé.

Ví dụ minh họa:

Cho hàm số y = 4x^3 - 3x - 1, hãy tính khoảng cách giữa 2 điểm cực trị của hàm số này.

Lời giải:

Với y = 4x^3 - 3x - 1 y ‘ = 12x^2 - 3 = 0 x = ½; y = -2 và x = -½; y = 0.

Suy ra tọa độ 2 điểm cực trị là A(½; -2); B(-½; 0).

Khoảng cách 2 điểm A, B là:

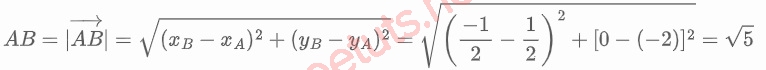
Vậy khoảng cách 2 điểm cực trị của hàm số y = 5

Công thức tính khoảng cách giữa hai số bất kỳ

Nếu bạn muốn tính khoảng cách giữa 2 số bất kỳ, hay chính là khoảng cách giữa hai điểm trên một trục số hoặc độ dài đoạn thẳng nối 2 điểm đó, hãy áp dụng công thức sau:

d = |a - b|

Ví dụ minh họa:

Trong hệ trục tọa độ Oxy, trên trục tung Ox, lần lượt lấy 2 điểm M, N với OM = 5, ON = 3, tính khoảng cách giữa hai điểm M và N.

d = |OM - ON| = |5 - 3| = 2.

Vậy khoảng cách giữa M và N là 2.

Công thức tính khoảng cách từ ảnh đến một thấu kính

Để tính khoảng cách từ ảnh của một vật thể đến thấu kính, ta có thể áp dụng công thức sau:

d = f(s - s’)/s’.

Trong đó:

• d: Khoảng cách từ ảnh đến thấu kính (m, inch).
• s: Kích thước thực của vật thể (m, inch).
• s’: Kích thước của ảnh (m, inch).
• f: Tiêu cự của thấu kính (m, inch).

Ví dụ minh họa:

Cho vật thể M có kích thước 3m, kích thước ảnh của vật thể trong thấu kính là 2m, thấu kính F có tiêu cự f = 1m, tính khoảng cách từ ảnh của vật thể M đến thấu kính F, biết ảnh của M được tạo ra trên mặt phẳng tiêu chuẩn của F.

Lời giải:

Áp dụng ct tính khoảng cách từ ảnh đến thấu kính, ta có:

d = 1.(3 - 2)/2 = ½

Vậy khoảng cách từ ảnh của vật thể M đến thấu kính F là ½ m

Bài tập liên quan đến công thức tính khoảng cách

• Bài 1: Cho 2 đường thẳng a: x - 3y + 4 = 0 và b: 2x + 3y - 1 = 0, tính khoảng cách giao điểm 2 đường thẳng a và b đến đường thẳng d: 3x + y + 16 = 0.

Lời giải:

Gọi A là giao điểm của 2 đường thẳng a và b, ta có tọa độ điểm A là nghiệm của hệ pt:

x - 3y + 4 = 0 và 2x + 3y - 1 = 0 x = -1 và y = 1.

Vậy tọa độ điểm A(-1,1)

Khoảng cách từ điểm A đến đường thẳng d là:

d(M,D) = |3(-1) + 1 + 16|/32 +12 = 14/10.

• Bài 2:

Trong trục tọa độ Oxyz, ta có hai mặt phẳng (P): x - 2y + z + 3 = 0 và (Q): x - 2y + z - 1 = 0, tính khoảng cách giữa (P) và (Q).

Lời giải:

Áp dụng ct tính khoảng cách giữa 2 mặt phẳng trong không gian, ta có:

d((P);(Q)) = |3 - (-1)|/12+(-2)2+12=4/6

Vậy, khoảng cách giữa 1 mặt phẳng (P) và (Q) là 4/6

• Bài 3: Trong trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 2z + 3 = 0, điểm M(0; 1; 3), tính khoảng cách từ điểm M đến mặt phẳng (P).

Lời giải:

Áp dụng ct tính khoảng cách từ 1 điểm đến mặt phẳng, ta có:

d(M(P)) = |0 + 2.2 - 2.3 +3|/12+22+(-2)2=1/3

Vậy khoảng cách từ điểm M đến mặt phẳng (P) là 1/3.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ tất cả các công thức tính khoảng cách thường gặp, hy vọng với những thông tin này, các em có thể dễ dàng hiểu được bản chất của các công thức và cách vận dụng chúng để giải các bài toán. Và đừng quên ghé thăm trang web của chúng tôi thường xuyên để tìm hiểu thêm kiến thức về các môn học khác nữa nhé!