Cách tính diện tích và thể tích hình lăng trụ đứng

Bài này sẽ tổng hợp kiến thức về hình lăng trụ đứng như: Khái niệm, các loại hình lăn trụ đứng, cách tính diện tích và thể tích.

Hình lăng trụ là một trong những loại hình học không gian được đưa vào chương trình giảng dạy toán phổ thông nói chung và toán lớp 8 nói riêng. Khi học nội dung này thì học sinh phải nắm vững các tính chất và công thức để vận dụng vào việc giải bài tập.

1. Hình lăng trụ đứng là gì?

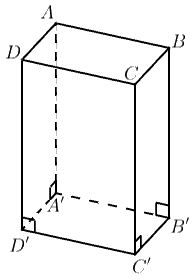
Hình lăng trụ đứng chính là các khối hình học có cạnh bên vuông góc với mặt đáy.

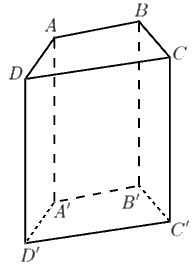
Hình vẽ trên đây là một ví dụ cho hình lăng trụ đứng. Nhìn vào hình vẽ chúng ta thấy hình lăng trụ trên có:

Bài viết này được đăng tại [free tuts .net]

• Có 8 đỉnh A,B,C,D,A’,B’,C’,D’ (số đỉnh tùy thuộc vào từng loại hình)
• Có các mặt bên đều là hình chữ nhật đó là AA’D’D, DCD’C’, BCB’C’, ABB’A’
• Có các đoạn thẳng song song với nhau và bằng nhau, chúng được gọi là các cạnh bên: AA’, BB’, CC’, DD’

Từ đây ta thấy hình hộp chữ nhật là một trường hợp đặc biệt của hình lăng trụ đứng, bởi nó có 8 đỉnh, các mặt bên đều là hình chữ nhật.

2. Tính chất của hình lăng trụ đứng

• Hai đáy của hình lăng trụ chính là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.
• Hình lăng trụ có các mặt bên vuông góc với mặt phẳng đáy và chúng đều là hình chữ nhật.
• Các cạnh bên của hình lăng trụ song song và bằng nhau, chúng vuông góc với mặt phẳng đáy và đó cũng chính là chiều cao của hình lăng trụ.

3. Hình lăng trụ đứng có những loại nào?

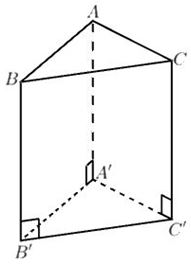
* Lăng trụ đứng tam giác: là hình lăng trụ có mặt phẳng đáy là hình tam giác

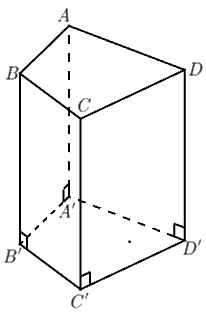
* Lăng trụ đứng tứ giác: là hình lăng trụ có đáy là một hình tứ giác

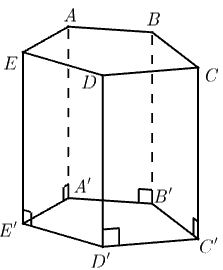
* Lăng trụ đứng ngũ giác: là hình trụ mà mặt phẳng đáy của nó có hình ngũ giác

* Hình hộp đứng: là hình trụ mà mặt phẳng đáy của nó chính là một hình bình hành

* Ngoài ra hình hộp chữ nhật hay hình lập phương cũng chính là những loại hình của lăng trụ đứng

4. Cách tính diện tích của hình lăng trụ đứng

Chúng ta cũng có hai phần như bài học trước, thứ nhất là diện tích xung quanh và thứ hai là diện tích toàn phần.

Cách tính diện tích xung quanh của lăng trụ đứng

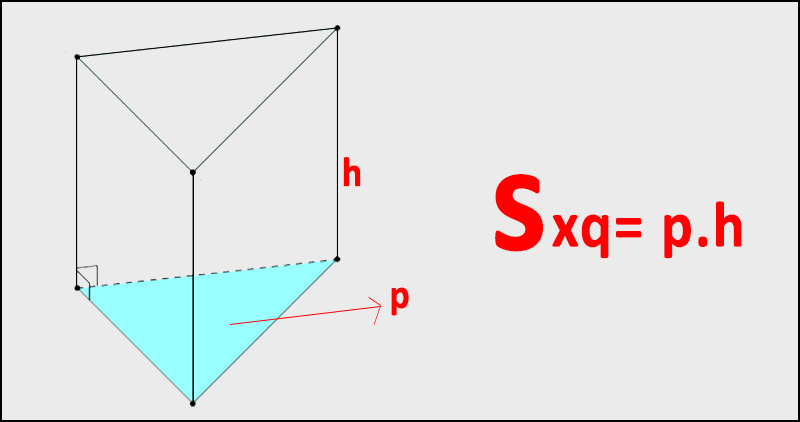
Diện tích xung quanh của hình lăng trụ đứng chính là tổng diện tích của tất cả các mặt bên của một hình lăng trụ.

Để tính được diện tích xung quanh của hình lăng trụ đứng chúng ta lấy chu vi đáy nhân với chiêu cao.

Công thức tổng quát:

(!! Sxq = P \times h !!)

Trong đó:

• Sxq là diện tích xung quanh
• P là chu vi đáy, tùy thuộc vào mỗi hình mà có cách tính chu vi khác nhau.
• h là chiều cao của lăng trụ đứng

Ví dụ: Cho một lăng trụ đứng tam giác có độ dài các cạnh đáy lần lượt là 5cm,6cm và 5cm. Tính diện tích xung quanh của lăng trụ đó biết chiều cao của lăng trụ đó là 7cm?

Bài giải:

Vì là hình lăng trụ hình tam giác nên để tính chu vi đáy thì ta sẽ áp dụng công thức tính chu vi hình tam giác.

Chu vi mặt đáy của lăng trụ đó là:

(!! P = 5+6+5=16(cm) !!)

Vậy, diện tích xung quanh của lăng trụ đó là:

(!! Sxq = 16 \times 7= 112(cm^2) !!)

Đáp số: 112 cm2

Cách tính diện tích toàn phần của lăng trụ đứng

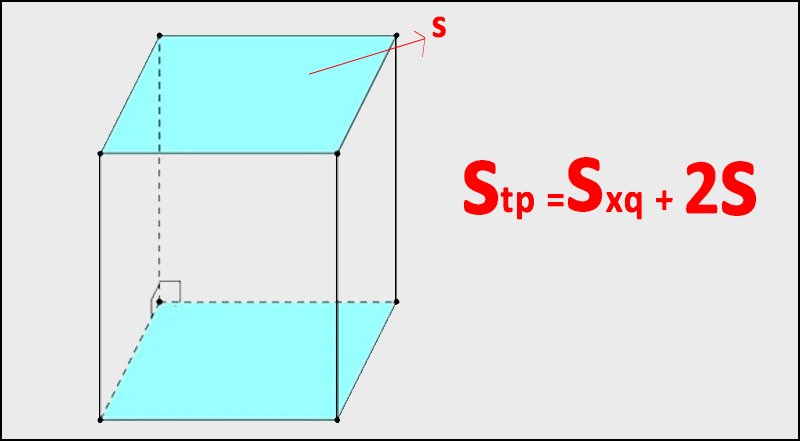
Diện tích toàn phần của hình lăng trụ đứng chính là bằng tổng diện tích của các mặt bên hình lăng trụ và hai mặt đáy của hình lăng trụ đó. Hay nói cách khác, diện tích toàn phần của hình lăng trụ là tổng diện tích xung quanh và diện tích hai mặt đáy.

Chúng ta có công thức tổng quát sau:

(!! Stp= Sxq + 2Sđáy !!)

Trong đó:

• Stp là diện tích toàn phần
• Sxq là diện tích xung quanh
• Sđáy là diện tích đáy, tùy thuộc vào mỗi hình mà có công thức tính khác nhau.

Ví dụ: Cho một hình lăng trụ đứng tứ giác, có mặt đáy của hình là một hình thang. Mặt đáy có chiều dài hai đáy lần lượt là 10cm, 13cm, và chiều dài hai cạnh bên là 8cm và 11cm, chiều cao của hình thang mặt đáy là 7cm. Hãy tính diện tích toàn phần của lăng trụ đó, biết chiều cao hình lăng trụ là 6cm?

Bài giải:

Ta sẽ áp dụng công thức tính chu vi hình thang để tính chu vi mặt đáy của hình lăng trụ tứ giác này.

Chu vi của mặt đáy hình thang là:

(!! P = 10+13+8+11= 42(cm) !!)

Diện tích mặt đáy của lặng trụ đó là:

(!! Sđáy = \frac{(13+10) \times 7}{2}=80,5 (cm^2) !!)

Diện tích xung quanh của hình lăng trụ đó là:

(!! Sxq = 42 \times 6= 252 (cm^2) !!)

Diện tích toàn phần của hình lăng trụ đó là:

(!! Stp = 252 + (2 \times 80,5)= 413 (cm^2) !!)

Đáp số: 413cm²

5. Cách tính thể tích của lăng trụ đứng

Thể tích của một hình lăng trụ đứng chính là phần không gian mà hình đó chiếm phải. Chúng ta tính thể tích của một hình lăng trụ bằng cách lấy diện tích đáy nhân với chiều cao.

Công thức chung:

(!! V = S \times h !!)

Trong đó:

• V là thể tích
• S là diện tích đáy
• h là chiều cao

Ví dụ: Cho một hình lăng trụ tam giác có diện tích đáy là 32cm² và chiều cao của hình lăng trụ là 5cm. Tính thể tích của hình lăng trụ đứng đó?

Bài giải:

Thể tích của hình lăng trụ đó là:

(!! S = 32 \times 5 = 160(cm^2) !!)

Đáp số: 160 cm²

Trên đây là bài viết tổng quát về hình lăng trụ, các loại hình lăng trụ đứng và các công thức liên quan kèm theo ví dụ. Hi vọng bài viết sẽ giúp các bạn hiểu rõ hơn về lăng trụ đứng để áp dụng nó vào việc giải bài tập một cách phù hợp nhất. Chúc các bạn học giỏi.