Hình tứ giác lớp 2: Định nghĩa, tính chất và phân loại

Hình tứ giác là một đa giác có 4 cạnh và 4 đỉnh, trong đó 2 cạnh bất kỳ không cùng nằm trên một đường thẳng và tổng 4 góc trong bằng 360 độ.

Trong toán học, hình tứ giác là một hình vô cùng đặc biệt và quan trọng, là nền tảng để cho các em phát triển bộ môn hình học sau này. Chính vì thế, trong bài viết hôm nay, hãy cùng freetuts đi sâu tìm hiểu tất tần tật những kiến thức liên quan đến hình tứ giác và một số dạng bài tập liên quan nha.

Định nghĩa hình tứ giác trong toán học

Định nghĩa hình tứ giác.

Trong hình học phẳng, tứ giác là một đa giác gồm có 4 cạnh và 4 đỉnh, và đa giác này không có 2 cạnh bất kỳ nào cùng nằm trên một đường thẳng.

Tính chất hình tứ giác trong toán học

Đối với tứ giác bất kỳ, có 2 tính chất quan trọng mà các em học sinh học toán cần phải ghi nhớ đó chính là:

Bài viết này được đăng tại [free tuts .net]

Tính chất 1: Góc của hình tứ giác

Tổng 4 góc trong của tứ giác bao giờ cũng bằng 360 độ.

Ví dụ minh họa:

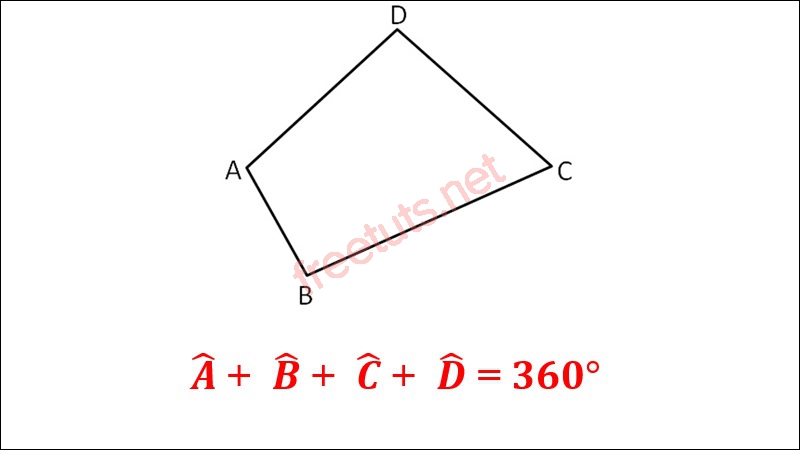
Tổng 4 góc của một tứ giác bằng 360 độ.

Tính chất 2: Đường chéo hình tứ giác

Trong một tứ giác lồi, 2 đường chéo sẽ cắt nhau tại 1 điểm thuộc miền trong của giác đó.

Ví dụ minh họa:

Đường chéo tứ giác lồi ABCD cắt nhau tại điểm E thuộc miền trong của ABCD.

Tổng hợp công thức tính chu vi và hình tứ giác trong toán học

Sau đây, freetuts sẽ chia sẻ một số công thức hình học quan trọng liên quan đến hình tứ giác mà các em cần nhớ.

Công thức tính chu vi hình tứ giác

Muốn tính chu vi của một tứ giác bất kỳ, bạn hãy cộng tổng số đo của 4 cạnh trong hình lại với nhau.

Công thức tính chu vi hình tứ giác: P = a + b + c + d.

Trong đó:

• P: Là chu vi hình tứ giác.
• a, b, c, d lần lượt là độ dài của 4 cạnh.

Lưu ý: Các cạnh phải có cùng đơn vị đo nhé.

Ví dụ minh họa:

Cho tứ giác ABCD có độ dài các cạnh lần lượt là AB = 4cm, BC = 6cm, CD = 8 cm, DA = 7cm, tính chu vi ABC.

Theo công thức tính chu vi tứ giác, ta có P(ABCD) = AB + BC + CD + DA = 4 + 6 + 8 + 7 = 25cm.

Công thức tính diện tích hình tứ giác

Không có một công thức chung nào để tính diện tích cho hình tứ giác, với mỗi loại tứ giác cụ thể, các em sẽ có từng công thức tính diện tích khác nhau như sau:

Công thức tính diện tích hình thang: S = h x ((a+b)/2)

Trong đó:

• a, b lần lượt là độ dài hai cạnh đáy,
• h là chiều cao.

Ví dụ minh họa:

Cho hình thang ABCD, có AB = 3cm, CD = 5cm, chiều cao h = 4cm, hãy tính diện tích hình thang

Lời giải:

Áp dụng công thức tính S hình thang, ta có S(ABCD) = 4 x ((3 + 5)/2) = 16 cm2

Công thức tính diện tích hình bình hành: S = b x h

Trong đó:

• b là độ dài cạnh đáy
• h là chiều cao.

Ví dụ minh họa:

Cho hình bình hành EFGH, có độ dài cạnh đáy GH = 5cm, chiều cao h = 3cm, tính diện tích hbh EFGH.

Lời giải:

Áp dụng công thức tính diện tích hình bình hành ta có: S(EFGH) = 5 x 3 = 15 cm2.

Công thức tính diện tích hình thoi: S = 1/2 x d1 x d2

Trong đó:

• d1. d2 lần lượt là độ dài hai đường chéo của hình thoi.

Ví dụ minh họa:

Cho hình thoi ABCD có độ dài hai đường chéo AC = 4cm, BD = 6cm, tính diện tích hình thoi này.

Lời giải:

Áp dụng công thức tính diện tích hình thoi, ta có: S(ABCD) = 1/2 x 4 x 6 = 12 cm2.

Công thức tính diện tích hình chữ nhật: S = a x b

Trong đó:

• a, b lần lượt là chiều dài và chiều rộng của hình chữ nhật.

Ví dụ minh họa:

Cho hình chữ nhật ABDC, có chiều dài AB = 7cm, chiều rộng BC = 3cm, tính diện tích hình chữ nhật này.

Lời giải:

Áp dụng công thức tính diện tích hình chữ nhật, ta có S(ABCD) = 7 x 3 = 21 cm2.

Công thức tính diện tích hình vuông: S = a x a

Trong đó:

• a là độ dài cạnh của hình vuông.

Ví dụ minh họa:

Cho hình vuông EFGH, có độ dài cạnh EF = FG = GH = HE = 4cm, hãy tính diện tích hình vuông này.

Lời giải:

Áp dụng công thức tính diện tích hình vuông, ta có S(ABCD) = 4 x 4 = 16 cm2.

Các loại hình tứ giác cơ bản và đặc biệt toán học

Hình tứ giác cơ bản

Có 4 loại tứ giác cơ bản như sau:

• Tứ giác đơn: Dấu hiệu nhận biết hình tứ giác đơn là tứ giác không có 2 cạnh không kề (cạnh đối) nào cắt nhau.
• Hình tứ giác lồi: Là tứ giác mà tất cả các số đo góc trong đều nhỏ hơn 180 độ, 2 đường chéo luôn nằm trong tứ giác. Hoặc các em có thể hiểu một cách đơn giản hơn là, tứ giác đơn là tứ giác luôn nằm trong 1 nửa mặt phẳng có bờ là bất kỳ một cạnh nào đó.
• Tứ giác lõm: Là tứ giác không lồi, có một góc trong lớn hơn 180 độ và một trong 2 đường chéo sẽ nằm ngoài tứ giác.
• Tứ giác không đều: Là một tứ giác mà không có bất kỳ cặp cạnh nào song song với nhau.

Hình tứ giác đặc biệt

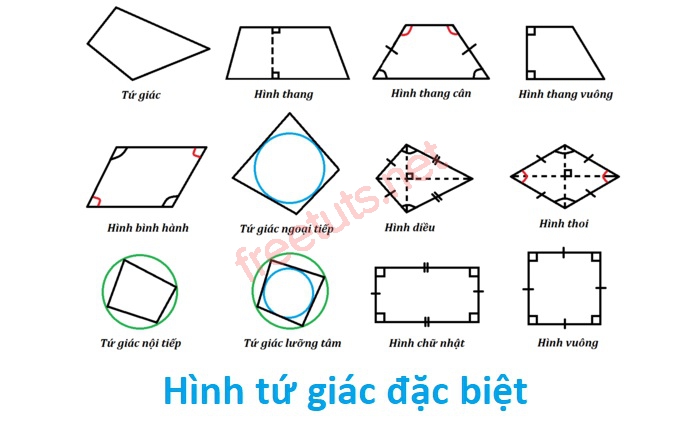
Các hình tứ giác đặc biệt.

Ngoài 3 dạng tứ giác cơ bản trên, thì thực tế cũng có một số tứ giác khá là đặc biệt như:

• Hình thang: Là tứ giác lồi có 3 cạnh đối diện song song.
• Hình thang cân: Là hình thang có số đo của 2 góc kề cùng một cạnh đáy bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm.
• Hình bình hành: Là tứ giác có 2 cặp cạnh đối song song bằng nhau, các góc đối bằng nhau, 2 đường chéo cắt nhau tại trung điểm.
• Hình thoi: Là tứ giác có 4 cạnh bằng nhau.
• Hình chữ nhật: Là tứ giác có 4 góc vuông.
• Hình vuông: Là tứ giác có 4 cạnh bằng nhau, 4 góc vuông, các cặp cạnh đối song song, hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
• Tứ giác nội tiếp: Là tứ giác có 4 đỉnh cùng nằm trên 1 đường tròn ngoại tiếp.
• Tứ giác ngoại tiếp: Là tứ giác có 4 cạnh cùng tiếp xúc với đường tròn nội tiếp.

Các dạng bài tập hình tứ giác lớp 2

Ngay bên dưới đây là một số các dạng bài tập thường gặp có liên quan đến hình tứ giác, mời các em học sinh và phụ huynh cùng tham khảo để biết cách giải chi tiết nha.

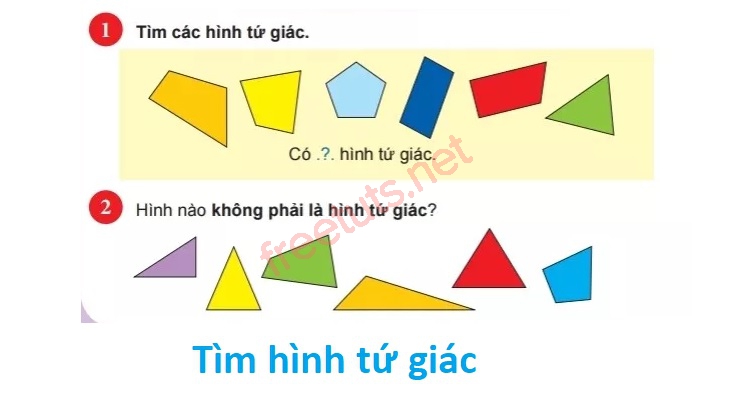
Dạng 1: Tìm hình tứ giác lớp 2

Đây là dạng bài tập cơ bản nhất cho các em học sinh lớp 2, để làm được dạng bài tập này, các e cần nắm vững lý thuyết định nghĩa hình tứ giác là gì nha.

Dạng 2: Dạng định nghĩa

Đây là một trong những dạng trắc nghiệm khá là phổ biến, nhằm kiểm tra khả năng ghi nhớ kiến thức của các em học sinh. Để giải được dạng câu hỏi này, các e cần phải nắm rõ dấu hiệu nhận biết hình tứ giác bằng cách ghi nhớ định nghĩa liên quan đến các dạng của tứ giác.

Ví dụ: Tứ giác có 2 cặp cạnh đối song song bằng nhau, 2 góc đối bằng nhau, 2 đường chéo cắt nhau tại trung điểm của mỗi đường là hình gì?

A. Hình chữ nhật.

B. Hình thoi.

C. Hình bình hành.

D. Hình thang.

Dựa vào kiến thức mà chúng tôi đã chia sẻ ở phần Các dạng hình tứ giác đặc biệt thì đáp án đúng sẽ là C. Hình bình hành.

Dạng 3: Dạng tính chu vi/diện tích của hình tứ giác

Đây là dạng câu hỏi vô cùng phổ biến. Để làm được tốt dạng này, các em cần ghi nhớ công thức tính chu vi, diện tích của hình tứ giác nha.

Ví dụ: Cho hình thoi ABCD có độ dài hai đường chéo là AC = 5cm, BD = 3cm, tính S hình thoi này.

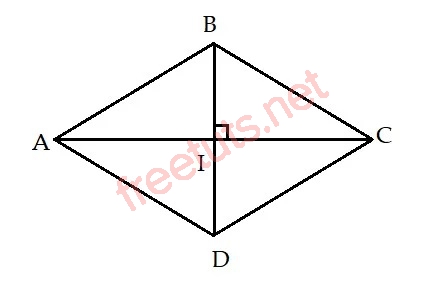
Lời giải:

Áp dụng công thức tính diện tích hình thoi, ta có: S(ABCD) = 1/2 x 5 x 3 = 7.5 cm2.

Dạng 4: Tính số đo các góc bất kỳ của hình tứ giác

Để có thể hoàn thành tốt các bài tập dạng này, các em cần nắm rõ kiến thức, tổng các góc trong của một tứ giác bằng 360 độ, tổng hai góc kề bù bằng 180 độ.

Ví dụ: Cho hình tứ giác ABCD như hình bên dưới, có số đo góc A = 50 độ, B = 117 độ, góc C = 71 độ, tính số đo góc kề bù với góc D.

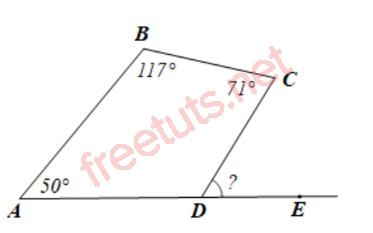
Lời giải:

Áp dụng tính chất góc của tứ giác, ta có Số đo góc D = 360 - 50 - 117 - 71 = 122 độ.

Vì số đo tổng hai góc kề bù bằng 180 độ, ta có góc kề bù với góc D = 180 - 122 = 58 độ.

Bài tập liên quan đến hình tứ giác

Bài tập 1: Cho tứ giác ABCD có góc A = 72 độ, góc B = 120 độ, góc C = 85 độ, tính số đo góc D.

Lời giải:

Áp dụng định lý tổng 4 góc trong của tứ giác bằng 360 độ, ta có

góc A + góc B + góc C + góc D = 360 độ, suy ra số đo góc D = 360 - A - B - C = 360 - 72 - 100 - 85 = 83 độ.

Bài tập 2: Cho hình thang ABCD, có AB = 6cm, CD = 9cm, chiều cao h = 5cm, hãy tính diện tích hình thang.

Lời giải:

S (ABCD) = 5 x ((6 + 9)/2) = 37.5 cm2

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ cho các em học sinh những kiến thức liên quan đến hình tứ giác, hy vọng những thông tin này sẽ giúp các em học tập hiệu quả hơn nè. Hẹn gặp lại các em trong các bài đăng tiếp theo để cùng nhau khám phá thêm nhiều kiến thức toán học thú vị khác nha.