Đường trung trực là gì? Tính chất, cách vẽ và bài tập áp dụng

Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng ấy và vuông góc với nó, mỗi đoạn thẳng chỉ có duy nhất một đường trung trực.

Đường trung trực là một phần kiến thức vô cùng quan trọng trong chương trình Toán lớp 7. Tuy nhiên cũng còn rất nhiều học sinh khá mơ hồ về nội dung này, nắm bắt được điều này, trong bài viết hôm nay, freetuts sẽ giúp các em ôn tập các kiến thức liên quan đến đường trung trực và cùng giải một số bài tập liên quan nhé.

Định nghĩa đường trung trực của một đoạn thẳng

Trong hình học, đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với chính nó là đường trung trực của đoạn thẳng này.

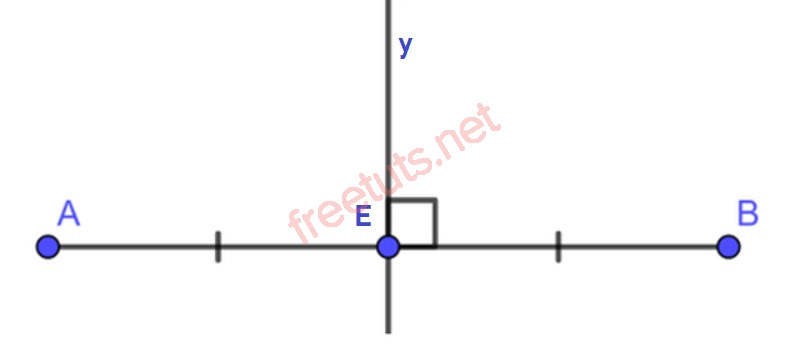
Hình ảnh minh họa về đường trung trực của đoạn thẳng.

Ví dụ: Cho đoạn thẳng AB, E là trung điểm của AB, đường thẳng y đi qua E và vuông góc với AB, lúc này, ta nói đường thẳng y là đường trung trực của AB.

Bài viết này được đăng tại [free tuts .net]

Tính chất đường trung trực của đoạn thẳng và tam giác

Cùng tìm hiểu về những tính chất đặc biệt của đường trung trực đối với đoạn thăng và các trường hợp đặc biệt của tam giác nha.

Tính chất, định lý đường trung trực của 1 đoạn thẳng

Tính chất 1: Cho một đoạn thẳng bất kỳ, điểm nằm trên đường trung trực của đoạn thẳng này thì luôn cách đều 2 đầu mút của đoạn thẳng đó.

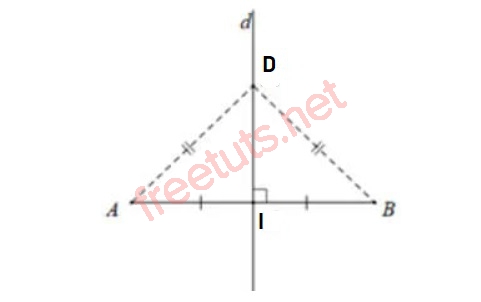
Ví dụ minh họa:

Cho đoạn thẳng AB, I là giao điểm của đường trung trực d và đoạn thẳng AB. D thuộc (d), lúc này ta có DA = DB.

Tính chất 2: Điểm cách đều hai đầu mút của một đoạn thẳng bất kỳ thì sẽ thuộc đường trung trực của đoạn thẳng ấy.

Từ tính chất này, ta có thể rút ra được nhận xét như sau:

Tập hợp các điểm cách đều 2 đầu mút của đoạn thẳng chính là đường trung trực của đoạn thẳng này.

Ví dụ minh họa:

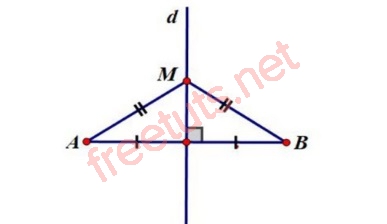
Cho đoạn thằng AB, điểm M không thuộc AB, MA = MB, suy ra M sẽ nằm trên đường trung trực của đoạn thẳng AB.

Tính chất đường trung trực của tam giác

Trong một tam giác bất kỳ, giao điểm của 3 đường trung trực là tâm của đường tròn ngoại tiếp tam giác đó.

Chứng minh như sau:

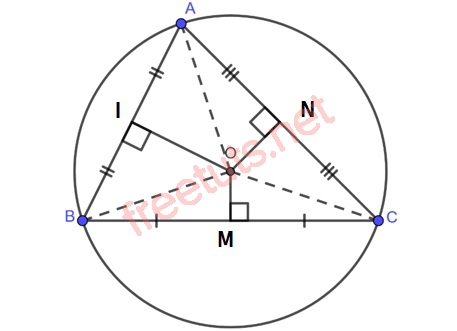
Cho tam giác ABC, OM, ON, OI lần lượt là 3 đường trung trực của 3 cạnh BC, AC và AB. Chứng minh O là tâm của đường tròn ngoại tiếp tam giác ABC.

Lời giải:

Xét tam giác OMC và tam giác OMB, ta có:

• OM chung
• Góc OMC = góc OMB = 90 độ (OM là trung trực của BC)
• BM = MC (M là trung điểm BC)

Nên ta có tam giác OMC = tam giác OMB, suy ra OC = OB (1)

Xét tam giác OBI và tam goác OIA, ta có:

OI chung

góc OIA = góc OIB = 90 độ (OI là trung trực BA)

IA = IB (I là trung điểm của AB)

Nên ta có tam giác OBI = tam goác OIA, suy ra OB = OA (2)

Từ (1) và (2), ta có OA = OB = OC.

Suy ra, O là tâm của đường tròn ngoại tiếp tam giác ABC (điều phải chứng minh)

Tính chất đường trung trực trong tam giác cân

Trong tam giác cân, đường trung trực ứng với cạnh đáy cũng chính là đường cao, đường phân giác và đường trung tuyến xuất phát từ đỉnh đối diện với cạnh đáy.

Chứng minh như sau:

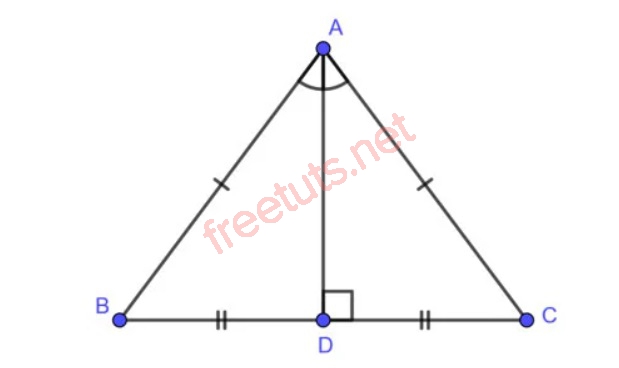
Cho tam giác cân ABC, AD là đường trung trực của cạnh đáy BC, chứng minh AD cũng là đường phân giác, đường cao và đường trung tuyến ứng với cạnh BC.

Lời giải:

Xét tam giác ADB và tam giác ADC, ta có:

AD: chung

BD = DC (AD là đường trung trực của BC)

AB = AC (Tam giác ABC cân)

Suy ra tam giác ABD = tam giác ADC, nên góc BAD = góc CAD

Suy ra AD chính là đường phân giác của góc BAC, ta có BD = DC, AD vuông góc với BC nên AD sẽ vừa là đường trung trực, đường phân giác, đường trung tuyến và đường cao ứng với cạnh BC (điều phải chứng minh).

Tính chất đường trung trực trong tam giác vuông

Trong tam giác vuông, giao điểm của 2 đường trung trực của 2 cạnh bên chính là trung điểm của cạnh huyền.

Ví dụ minh họa:

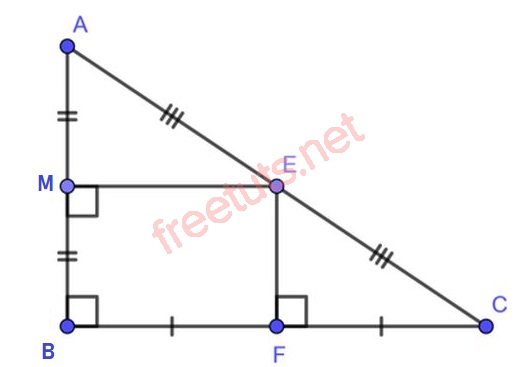
Cho tam giác ABC vuông tại B, EF là đường trung trực của cạnh BC, EM là đường trung trực của cạnh AB, E thuộc AC, lúc này ta có EA = EC hay nói cách khác, E chính là trung điểm của cạnh AC.

Cách vẽ đường trung trực của một đoạn thẳng

Có hai cách vẽ đường trung trực của một đoạn thẳng như sau:

Cách 1: Dùng thước kẻ và eke

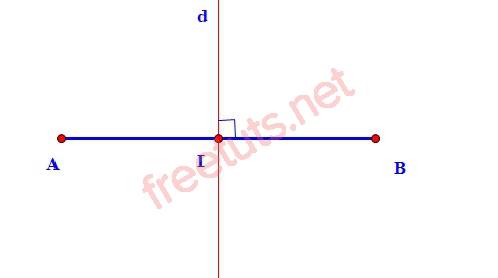
• Bước 1: Vẽ đoạn thẳng AB bất kỳ, xác định trung điểm I của AB, sao choIA = IB.
• Bước 2: Từ trung điểm N, dựng đường thẳng (d) vuông góc với AB, lúc này ta có (d) là đường trung trực của đoạn AB.

Cách 2: Dùng thước kẻ và compa

Ngoài cách dùng thước kẻ để xác định đường vuông góc trên, chúng ta có thể sử dụng compa để vẽ đường trung trực thông qua các bước sau:

• Bước 1: Vẽ đoạn thẳng AB
• Bước 2: Dùng compa lần lượt vẽ 2 đường tròn tâm A, B có bán kính bằng nhau.
• Bước 3: Hai đường tròn vừa vẽ sẽ giao nhau tại hai điểm (M và N), dùng thước nối hai điểm M và N ta sẽ có được đường trung trực của đoạn thẳng AB.

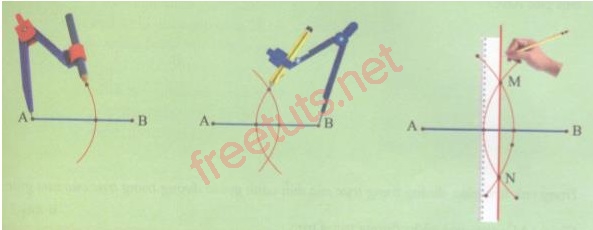
Chi tiết các bước vẽ đường trung trực bằng compa.

Dạng bài tập liên quan đến đường trung trực

Như vậy, các em đã nắm được các kiến thức quan trọng về đường trung trực rồi đúng không nào, bây giờ hãy cùng vận dụng chúng để đi giải một số dạng bài tập mà freetuts đã tổng hợp ngay bên dưới đây nha.

Dạng 1: Chứng minh đường trung trực

Để chứng minh đường thẳng (d) bất kỳ là đường trung trực của đoạn thẳng AB, các em hãy chứng minh một điểm nằm trên (d) cách đều 2 đầu mút AB.

Ví dụ minh họa:

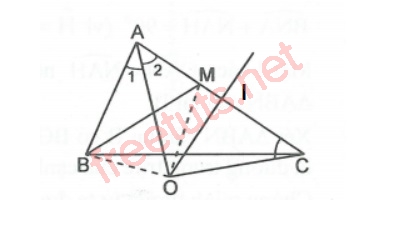
Cho tam giác ABC, AB < AC. Điểm M thuộc AC, sao cho MC = AB, đường trung trực của AC cắt đường phân giác của góc A tại điểm O. Chứng minh rằng O thuộc đường trung trực của đoạn BM.

Lời giải:

Để chứng minh O nằm trên đường trung trực của BM, chúng ta hãy cùng chứng minh OB = OM nha.

Ta có, điểm O thuộc đường trung trực của AC nên ta có OA = OC.

Nên tam giác OAC cân tại O, ta có góc OAC bằng góc OCA (1)

Mà O thuộc đường phân giác góc A, nên ta có góc OCA = OAB (2)

Kết hợp (1) và (2) ta có:

góc OCA = góc OAB (3)

Xét tam giác ABO và tam giác CMO, ta có:

• AB = CM (đề cho)
• góc OCA = góc OAB (đã chứng minh ở trên)
• OA = OC

Suy ra, tam giác ABO = tam giác CMO (cạnh.góc.cạnh)

Suy ra OB = OM, vậy điểm O nằm trên đường trung trực của BM (điều phải chứng minh)

Dạng 2: Chứng minh hai đoạn thẳng bằng nhau

Để làm tốt dạng toán này, các em cần sử dụng tính chất “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều 2 đầu mút của đoạn thẳng ấy.”

Ví dụ: Cho tam giác ABC, gọi E,F lần lượt là trung điểm của AB và AC. Đường trung trực của AB và AC cắt BC lại M và N. Tam giác ABM và tam giác ANC là tam giác gì?

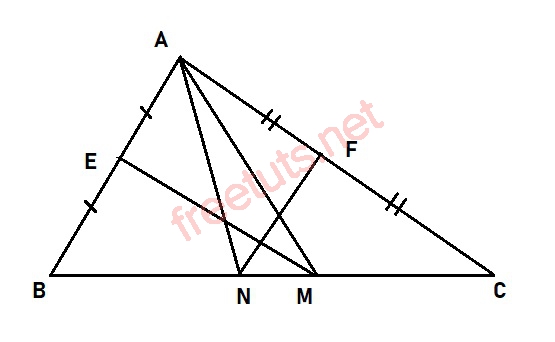
Lời giải:

Xét tam giác ANF và tam giác CFN, ta có:

• FA = FC (F là trung điểm AC)
• góc NFC = góc NFA = 90 độ (NF là đường trung trực cạnh AC)
• Cạnh NF chung

Suy ra tam giác ANF = tam giác CFN, suy ra AN = CN

Xét tam giác ANC có AN = NC, nên suy ra tam giác ANC cân tại N.

Xét tam giác MEB và tam giác MEA, ta có:

• ME chung
• EA = EB (E là trung điểm AB)
• góc MEB = góc MEA = 90 độ (ME là đường trung trực của cạnh AB)

Suy ra tam giác MEB = tam giác MEA, suy ra cạnh MB = MA

Xét tam giác MAB có MA = MB, nên tam giác MAB là tam giác cân tại M.

Dạng 3: Áp dụng tính chất đường trung trực trong bài toán tìm cực trị

Đối với dạng toán này, các em hãy áp dụng tính chất đường trung trực để thay đổi độ dài đoạn thẳng thành một đoạn thẳng khác bằng nó, sau đó kết hợp với bất đẳng thức trong tam giác để tìm giá trị lớn nhất hoặc nhỏ nhất.

Ví dụ minh họa:

Cho hai điểm M, N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng y, tìm vị trí điểm A trên đường thẳng y sao cho giá trị của AM + AN là nhỏ nhất.

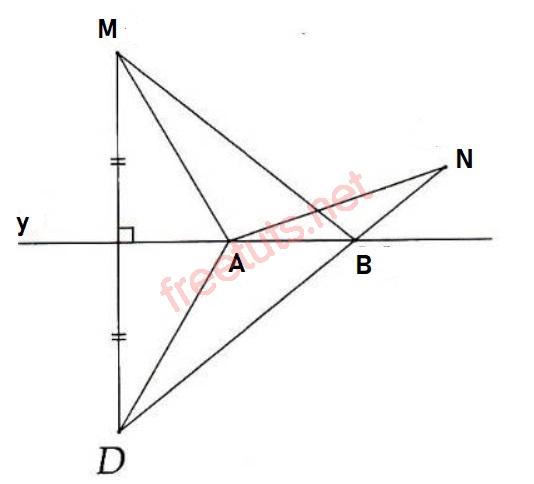
Lời giải:

Lấy D là điểm đối xứng với M qua d, áp dụng tính chất đường trung trực, ta có AD = AM.

Do đó, AM + AN = AD + AN.

Gọi B là giao điểm của DM và đường thẳng (y).

Nếu A không trùng B, ta xét:

Tam giác NAD, có: AD + AN > DN hay

AM + AN > DN (1)

Nếu A trùng B thì:

AM + AN = AB + BN = BD + BN = DN (2)

Từ (1) và (2) ta suy ra, khi điểm A trùng B hoặc A là giao điểm của DN và (y) thì AM + AN đạt giá trị nhỏ nhất. (điều phải chứng minh)

Dạng 4: Bài toán liên quan đến đường trung trực trong tam giác vuông

Để giải được dạng toán này, các em cần nắm rõ tính chất đường trung trực của tam giác vuông nhé.

Ví dụ minh họa:

Cho tam giác AMN vuông tại A, AN = 6cm, AM = 8cm, E là giao điểm của 3 đường trung trực của tam giác AMN. Tính khoảng cách EA, EM và EN =?

Lời giải:

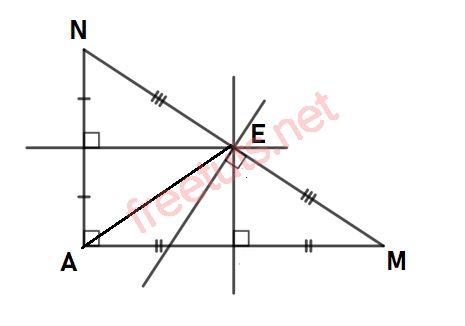
Vì E là giao điểm của 3 đường trung trực tam giác AMN, nên ta có EA = EM = EN.

Xét tam giác AMN vuông tại A, nên E là trung điểm của cạnh huyền MN.

Áp dụng định lý pytago cho tam giá AMN, ta có:

MN^2 = AM^2 + AN^2 = 6^2 + 8^2 = 100

Suy ra MN = 10 cm.

Mà EA = EM = EN = 1/2MN = 1/2 x 10 = 5 cm.

Dạng 5: Bài toán liên quan đến đường trung trực trong tam giác cân

Đối với các dạng toán liên quan đến đường trung trực trong tam giác cân, các em cần nắm vững tính chất đường trung trực của tam giác cân đã nêu ở trên để có thể áp dụng vào giải các bài tập nha.

Ví dụ minh họa:

Cho 3 tam giác cân ABC, MBC, NBC có chung cạnh đáy BC. Chứng minh rằng ba điểm A, M, N thẳng hàng.

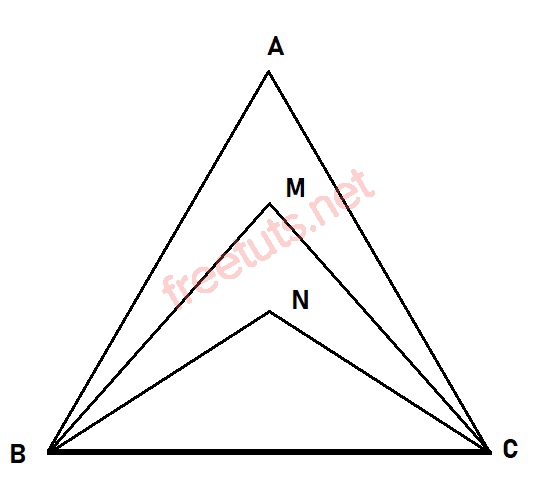
Lời giải:

Xét tam giác ABC cân tại A, nên ta có AC = AB, suy ra A thuộc đường trung trực của BC. (1)

Xét tam giác MBC cân tại M, nên ta có MB = MC, suy ra M thuộc đường trung trực của BC. (2)

Xét tam giác NBC cân tại N, nên ta có NB = BC, suy ra N thuộc đường trung trực của BC. (3)

Từ (1), (2), (3), suy ra A, M, N thuộc đường trung trực của BC nên A, M, N thẳng hàng.

Hỏi đáp về đường trung trực

Đường trung trực tiếng Anh là gì?

Đường trung trực trong tiếng Anh là “midperpendicular”

Trong tam giác thường, đường trung trực và đường trung tuyến có phải là một không?

Điều này hoàn toàn là sai nhé, nó chỉ đúng với trường hợp tam giác này là tam giác cân thôi nè.

Một đoạn thẳng có bao nhiêu đường trung trực?

Vì đường trung trực của đoạn thẳng là đường đi qua trung điểm và vuông góc với chính nó nên mỗi đoạn thẳng chỉ có duy nhất một đường trung trực mà thôi.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ các kiến thức liên quan đến đường trung trực bao gồm định nghĩa, tính chất và các dạng bài tập liên quan. Hy vọng những thông tin này sẽ hữu ích đối với các bạn học sinh, chúc các em đạt kết quả cao trong học tập nha.