Rút gọn biểu thức lớp 8 - 9, tổng hợp đầy đủ và bài tập

Cách rút gọn biểu thức chứa căn, biểu thức logarit, biểu thức lượng giác và tổng hợp một số bài tập liên quan cùng cách giải chi tiết, tham khảo tại đây.

Rút gọn biểu thức là một bài học vô cùng quan trọng trong chương trình toán cấp 2, nhờ việc rút gọn các biểu thức có thể giúp các em dễ dàng giải nhiều dạng bài tập nâng cao liên quan. Trong bài viết hôm nay, hãy cùng freetuts tìm hiểu chi tiết cách rút gọn đối với từng biểu thức khác nhau nha.

Rút gọn biểu thức chứa căn thức bậc hai, bậc ba

Đối với dạng bài tập rút gọn một biểu thức có chứa căn, các em hãy làm theo các bước sau nha:

• Bước 1: Tìm điều kiện để biểu thức xác định (nếu đề bài chưa có), A có nghĩa khi A 0.
• Bước 2: Biến đổi các biểu thức trong căn về dạng A^2, A^3, A^4,...để có thể tiến hành rút gọn các biểu thức này. Nếu biểu thức chứa các căn thức giống nhau thì đặt căn thức đó làm ẩn phụ và đưa về dạng bài toán rút gọn với ẩn phụ mới.

Lưu ý:

Bài viết này được đăng tại [free tuts .net]

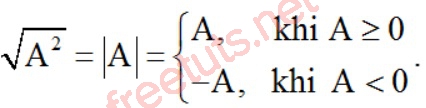
Hãy nắm vững một số tính chất của căn thức để có thể áp dụng vào việc rút gọn bt chức căn nha:

Ví dụ minh họa:

Hãy rút gọn bt sau: A = 100a2+a .

Lời giải:

A = 100a2+a =102.a2 + a = (10a)2 + a = |10a| + a.

• Nếu a < 0, thì |10a| = -10a, A = -10a + a = -9a.
• Nếu a > 0 thì |10a| = 10a, A = 10a + a = 11a.

Rút gọn biểu thức chứa logarit

Muốn thực hiện được các bài toán rút gọn một biểu thức có chứa logarit, các em cần vận dụng quy tắc, tính chất của công thức logarit kết hợp với các công thức lũy thừa đã học để có thể hoàn thành được bài tập dạng này nha.

Ví dụ minh họa:

Hãy rút gọn M = 3log94 + log36

Lời giải:

Ta có:

log94 + log36 = 1/2log34 + log36 = log32 + log36 = log312

Vậy M = 3log94 + log36= 3log312 = 12

Rút gọn biểu thức phân số

Nếu gặp một biểu thức có chứa mẫu cần rút gọn, các em hãy làm theo thứ tự các bước hướng dẫn sau của freetuts nha:

• Bước 1: Tìm điều kiện xác định của biểu thức, A/B có nghĩa khi B khác 0.
• Bước 2: Phân tích tử và mẫu số thành nhân tử rồi thực hiện rút gọn, nếu biểu thức chưa nhiều biểu thức con, các em hãy rút họn từng biểu thức con trước nhé.

Ví dụ minh họa:

Cho Q = (1- xx 1-x + x ).(1-a1-a)2

Lời giải:

Q có nghĩa khi x 0, 1 - a 0, 1-x 0 x 0 và x 1.

Đặt x = t, suy ra, x = t^2.

Q = (1-t31-t+ t)(1-t1-t2)2 =[(1-t)(1+t+t2)1-t+ t][1-t(1-t)(t+1)]2 = (1 + t + t^2 + t)(1t+1)2

= (1 + t + t^2 + t)(1/(1 + t + t^2 + t)) = 1.

Rút gọn biểu thức lượng giác

Khi gặp dạng toán rút gọn một biểu thức chứa hàm lượng giác, các em chỉ cần nắm vững công thức lượng giác từ cơ bản đến nâng cao để có thể biến đổi biểu thức một cách linh hoạt, từ đó có thể triệt tiêu các giá trị lượng giác không đặc biệt để đưa về giá trị lượng giác của các cung đặc biệt.

Ví dụ minh họa:

Cho biểu thức A = cos10x + 2cos^2(4x) + 6coss3x.cosx - cosx - 8 cosx.cos^3(3x), hãy rút gọn A.

Lời giải:

A = cos10x + 2cos^2(4x) + 6coss3x.cosx - cosx - 8 cosx.cos^3(3x)

A = cos10x + 1 + cos8x - cosx - 2(4cos^3(3x) - 3cos3x).cosx

A = 2.cos9x.cosx + 1 - cosx - 2.cos9x.cosx = 1 - cosx.

Bài tập rút gọn biểu thức và cách giải

Sau khi đã nắm được các dạng rút gọn bt ở trên, bây giờ, các em hãy vận dụng nó để giải một số bài tập sau nha.

Bài tập rút gọn biểu thức lớp 8:

Rút gọn bt sau: A = x + 2x-1 -x 2 2x-1

Lời giải:

A = x + 2x-1 -x -2 x-1

A = x -1+ 2x-1-1 -x -1-2 x-1+1

A = (x-1+1)2 -(x-1-1)2

A = |x-1+1| - |x-1-1|

A = x-1+1 - x-1+1 = 2.

Bài tập rút gọn biểu thức lớp 9 nâng cao: 

Cho biểu thức P = 2lna + 3logee - 3/lna - 2/logae, a > 0, a khác 1, hãy rút gọn P.

Lời giải:

Ta có:

P = 2lna + 3logee - 3/lna - 2/logae = 2lna + 3.(1/lna) - (3/lna) - 2logae

P = 2lna + 3/lna - 3/lna - 2lna = 0.

Bài tập rút gọn biểu thức lượng giác 11 nâng cao:

Rút gọn các biểu thức sau:

A = (sinx + sin3x + sin5x)/(cosx + cos3x + cos5x)

A = (sinx + sin5x + sin 3x)/(cosx + cos5x + cos3x)

A = (2sin3x.cos2x + sin3x)/(2coss3x.cos2x + cos3x)

A = (sinx(2cos2x + 1)/(cos3x(1cos2x - 1)

A = sin3x/cos3x

A = tan3x.

Bài tập tự luyện rút gọn biểu thức

Và bây giờ, các em hãy thử sức mình với một số bài tập tự luyện ngay dưới đây nha.

Bài 1: Chứng minh biểu thức sau không phụ thuộc vào x:

A = Cos^2(x - pi/3) + cos2x + cos2(x + pi/3)

B = Cosx + cos(x + 2a) + cos(x + 4a) + cos(x + 6a)

Bài 2: Rút gọn các biểu thức sau:

A = 2x/(x +3) -(x - 1)/(3 - x ) - (3 -11x )/(x - 9)

B = 2log212 + 3log25 -log215-log2150

C = (2x - 3)(4x + 6) - (6 - 3x)(4x -2)

D = (x - 1)/(x - 3) - (7x - 9)(x - 9)

Như vậy. qua bài viết trên, freetuts.net đã chia sẻ cách rút gọn biểu thức thường gặp trong chương trình toàn lớp 8 và lớp 9. Hy những thông tin này sẽ giúp các em củng cố lại được kiến thức và có thể hoàn thành tốt các dạng bài tập liên quan.