Tiệm cận ngang: công thức, cách tìm TCN của đồ thị hàm số

Tiệm cận ngang là khái niệm dùng để diễn tả hành vi của một đồ thị hàm số bất kỳ khi x tiến tới vô cùng, từ đó có thể biết thêm nhiều thông tin về hàm số này.

Tiệm cận ngang là một kiến thức vô cùng quan trọng trong chương trình toán THPT, tuy nhiên, đối với nhiều em học sinh chắc hẳn còn chưa nắm rõ về kiến thức này. Chính vì vậy, trong bài viết hôm nay, freetuts sẽ giúp các em ôn lại các kiến thức về đường tiệm cận ngang, cách giải cũng như một số dạng bài tập cơ bản nha.

Vai trò của đường tiệm cận ngang trong đại số

Định nghĩa đường tiệm cận ngang

Tiệm cận ngang là một khái niệm quan trọng trong toán học dùng để mô tả hành vi của một đồ thị hàm số y = f(x) xác định trên a đến vô cùng. Có hai loại tiệm cận ngang là TCN dương và đường TCN âm, cụ thể như sau:

• Nếu limx→+∞ y = b thì y = b là đường TCN của đồ thị hàm số y = f(x), với x xác định trên khoảng từ (a, +∞)
• Nếu lim_x→−∞ y = b thì y = b là đường TCN của đồ thị hàm số y = f(x), với x xác định trên khoảng từ (a, -∞)

Và như vậy, đối với một hàm số y = f(x) bất kỳ, ta chỉ có tối đa là 2 đường TCN và cũng có thể không có đường TCN nào cả.

Bài viết này được đăng tại [free tuts .net]

Tại sao phải tìm đường tiệm cận ngang của một hàm số?

Bây giờ, hãy cùng tìm hiểu tại sao đường TCN lại là một kiến thức quan trong trong chương trình toán THPT nha.

Khi biết được đường TCN của một đồ thị hàm số, các em sẽ nắm được những thông tin sau:

• Biết được hướng tiếp cận của đồ thị hàm số với đường TCN thì theo hướng âm hay hướng dương.
• Biết được đặc điểm của đồ thì hàm số y = f(x) bất kỳ, nếu hàm số y = f(x) có đường tiệm cận ngang dương, chúng ta có thể rút ra được kết luận quan trọng là giá trị của hàm số đó sẽ không bao giờ nhỏ hơn TCN đó và ngược lại, nếu đường TCN âm, giá trị của hàm số y = f(x) sẽ không bao giờ lớn hơn đường tiệm cận đó.
• Và một điều quan trọng không kém là đường tiệm cận sẽ giúp chúng ta xác định được các đường bị chặn của hàm số bất kỳ.

Các công thức tính tiệm cận ngang

Tìm tiệm cận ngang của đồ thị hàm phân thức hữu tỉ

Nếu muốn tìm đường TCN của một hàm số phân thức hữu tỉ, các em hãy áp dụng công thức dưới đây nha:

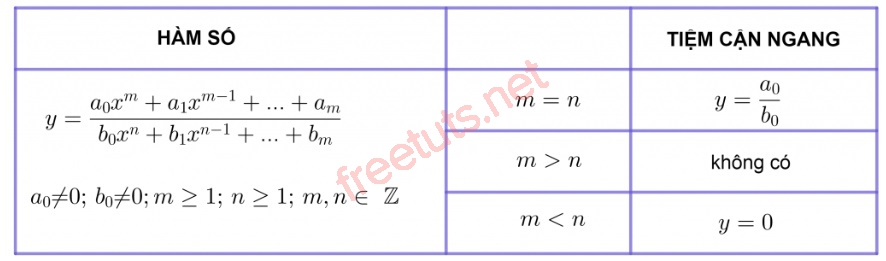
Tìm tiệm cận ngang của đồ thị hàm phân thức vô tỷ

Để tính TCN của hàm phân thức vô tỷ, hãy áp dụng công thức theo bảng sau nè.

Tìm tiệm cận ngang của hàm số căn thức

Cho hàm số y = f(x) với f(x) là hàm số chứa căn thức bất kỳ. Tìm tập xác định D của hàm số f(x).

Để hàm số y = f(x) có tồn tại TCN thì:

• Trong tập xác định D của hàm số y = f(x) phải chứa âm vô cùng (−∞) hoặc dương vô cùng (+∞).
• Một trong 2 giới hạn là limx→-∞ y hoặc limx→+∞ là số hữu hạn.​

Cách tìm tiệm cận ngang của một đồ thị hàm số bất kỳ

Sử dụng máy tính bỏ túi Casio để tìm TCN.

Hướng dẫn cơ bản

Để tìm được đường tiệm cận ngang của một đồ thị hàm số y = f(x) bất kỳ, các em hãy làm theo hướng dẫn sau đây nha:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính giới hạn của hàm số đó tại vô cực, từ đó sẽ xác định đường đường TCN cần tìm.

Cách tính đường tiệm cận ngang bằng máy tính bỏ túi Casio

Hiện nay, các em có thể dễ dàng tìm đường TCN của một hàm số bất kỳ bằng máy tính bỏ túi casio đấy nha. Hãy cũng heo dõi hướng dẫn sau để biết thêm chi tiết nè.

Bước 1: Tìm giá trị gần đúng của lim_x →−∞y và lim_x →+∞y.

Bước 2:

• Tìm giá trị của lim_x →+∞y, ta tường lấy x = 10 mũ 9, kết quả sẽ là giá trị gần đúng của lim_x →+∞y.
• Tìm giá trị của lim_x →−∞y, ta tường lấy x = -10 mũ 9, kết quả sẽ là giá trị gần đúng của lim_x →−∞y.

Bước 3: Sử dụng chức năng CALC trên máy tính bỏ túi Casio để tìm giá trị hàm số tại giá trị tương ứng của x.

Ví dụ minh họa:

Cho đường TCN của đồ thị hàm số y = (1-x)/(3x+1), hãy tìm đường TCN của đồ thị hàm số y.

Lời giải:

Xét hàm số y = (1-x)/(3x+1), có TXĐ: x thuộc R\{-1/3}

• Nhập hàm số y = (1-x)/(3x+1) vào máy tính, chọn phím CALC, nhập giá trị x = 10 mũ 9, bấm dấu =, lúc này ta sẽ được kết quả = -0.3333, xấp xỉ bằng -1/3
• Nhập hàm số y = (1-x)/(3x+1) vào máy tính, chọn phím CALC, nhập giá trị x = -10 mũ 9, bấm dấu =, lúc này ta sẽ được kết quả = -0.3333, xấp xỉ bằng -1/3

Vậy ta có:

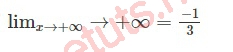
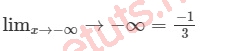
Lúc này, ta có thể đưa ra kết luận, hàm số có 1 TCN là đường thẳng y = -1/3

Cách tính đường tiệm cận ngang dựa vào bảng biến biên

Ngoài 2 cách trên để tìm TCN, các em có thể dễ dàng xác định được đường TCN của một đồ thị hàm số bất kỳ dựa vào bảng biến thiên với các bước như sau:

Bước 1: Đầu tiên, các em hãy tìm tập xác định (tập nghiệm) của hàm số này dựa vào bảng biến thiên.

Bước 2: Dựa vào bảng biến thiên, hãy suy ra giới hạn khi giá trị x đi đến biên của miền xác định.

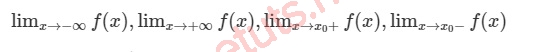
Bước 3: Rút ra kết luận.

Ví dụ minh họa:

Cho hàm số f(x) xác định liên tục, có bảng biến thiên như sau, hãy xác định đường TCN của hàm số f(x)

Hướng dẫn giải:

Dựa vào bảng biến thiên, ta có

lim f(x) khi x →−∞ = 5, vậy y = 5 là TCN, lim f(x) khi x →+∞ = 2, vậy y = 2 cũng là TCN.

Vậy, đồ thị hàm số có 2 đường TCN là y = 2 và y = 5

Dạng bài tập liên quan đến tiệm cận ngang và cách giải

Ngay bên dưới đây, freetuts đã tổng hợp một số dạng bài tập thường gặp về đường TCN, mời các em cùng tham khảo nha.

Dạng 1: Xác định tiệm cận của hàm số

Đối với dạng bài tập này, các em chỉ cần nắm vững lý thuyết đường tiệm cận ngang là có thể giải được một cách đơn giản rồi nè.

Ví dụ minh họa:

Hãy tìm đường TCN của đồ thị hàm số sau:

Lời giải:

Xét hàm số y, có TXĐ D = R\{-1;1}. ta có:

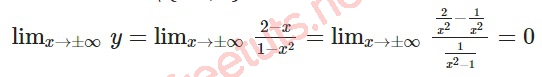
Vậy y = 0 là đường TCN cần tìm của đồ thị hàm số y.

Dạng 2: Tìm m để hàm số có tiệm cận thỏa mãn điều kiện bất kỳ cho trước

Đối với dạng toán này, các em hãy áp dụng phương pháp sau để tìm được lời giải nhé:

• Bước 1: Tìm điều kiện của tham số đã cho để hàm số được xác định.
• Bước 2: Tìm các đường tiệm cận của hàm số đó.
• Bước 3: Dựa vào điều kiện cho trước để tìm tham số.

Ví dụ: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số sau có hai TCN:

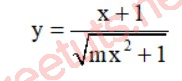
Hướng dẫn giải:

• Với m > 0, x →+∞, ta có:

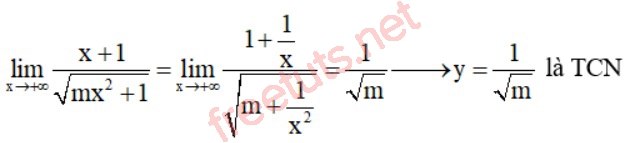
• Với m > 0, x →-∞, ta có:

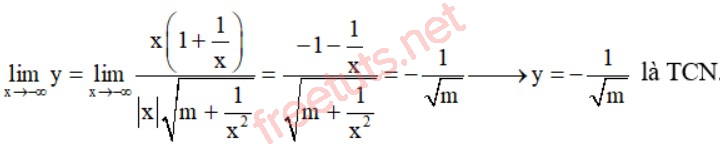
• Với m < 0, hàm số có TXĐ là một đoạn nên đồ thị sẽ không có đường TCN.

Kết luận: Như vậy, với m > 0 thì đồ thị đã cho sẽ có 2 đường tiệm cận ngang.

Bài tập tìm đường tiệm cận ngang của một đồ thị hàm số

Bài tập 1: Cho hàm số y = 5/(x-1), đường TCN của hàm số y là đường thẳng có phương trình?

Lời giải:

Áp dụng định nghĩa đường TCN của đồ thị hàm số y = (ax + b)/(cx +d) có phương trình là y = a/c.

Vậy với y = 5/(x-1), ta có a = 0, c =1, vậy đồ thị hàm số đã cho có TCN là y =0/1 = 0.

Bài tập 2:

Tìm đường TCN của đồ thị hàm số sau:

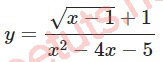
Lời giải:

Có y = y0 là TCN của đồ thị hàm số y =f(x) nếu:

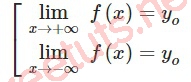
Ta có:

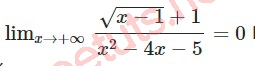
Vậy y = 0 là TCN của đồ thị hàm số đã cho.

Bài tập 3: Đồ thị hàm số sau có bao nhiêu đường TCN?

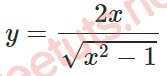
Lời giải:

Ta có:

Vậy đồ thị đã cho có 2 đường TCN lần lượt là y = 2 và y = -2.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ tất cả những kiến thức quan trọng liên quan đến đường tiệm cận ngang cũng như một số dạng bài tập quen thuộc, hy vọng các em sẽ củng cố thêm được kiến thức cho mình và có thể hoàn thành tốt các dạng bài tập liên quan đến đường TCN nha.