Kiến thức 3 đường conic (Elip, Hypebol, Parabol) và các dạng bài tập

3 đường conic bao gồm đường elip, đường hypebol và đường parabol, mỗi đường sẽ có một phương trình chính tắc riêng và được ứng dụng nhiều trong đời sống.

Đường conic là một đường cong bậc hai được tạo thành bằng cách cắt một mặt nón tròn xoay bằng một mặt phẳng. Có 3 đường conic cơ bản là đường elip, hypebol và parabol, hãy cùng freetuts tìm hiểu về 3 đường này ngay bên dưới đây nha.

Kiến thức 3 đường Conic - Đường elip

Khái niệm đường Elip trong toán học

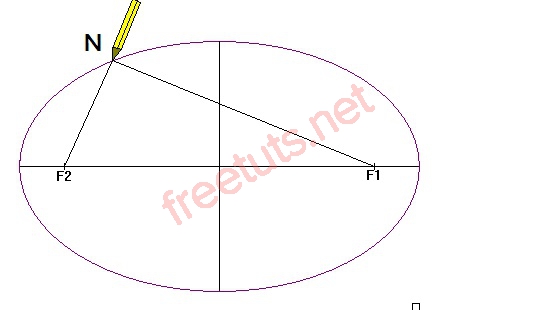
Hình ảnh đường Elip.

Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2a, với a > 0.

Đường elip (elip) là tập hợp các điểm N trong mặt phẳng sao cho NF1 + NF2 = 2b, trong đó b là số cho trước lớn hơn a. Và hai điểm F1, F2 được gọi là 2 tiêu điểm của elip này.

Bài viết này được đăng tại [free tuts .net]

Phương trình chính tắc của đường Elip

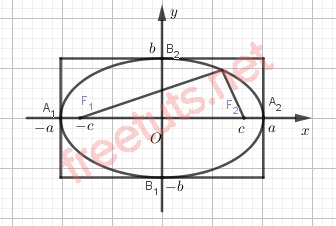
Phương trình chính tắc của E.

Trong mặt phẳng bất kỳ, xét đường elip (E) bao gồm tập hợp các điểm N sao cho NF₁ + NF₂ = 2a, F₁F₂ = 2b ( với a > b > 0).

Chọn hệ trục tọa độ Oxy có gốc đi qua trung điểm F₁F₂, Oy là đường trung trực của F₁F₂, F₂ nằm trên tia Ox, hai tiêu điểm của elip lần lượt là F₁(-a ; 0) và F₂(a ; 0).

Lúc này, ta sẽ có phương trình chính tắc của E như sau:

x2/a2 + y2/b2 = 1, với a > b > 0, c2 = a2 + b2, 2c = F1F2

Ví dụ minh họa:

1. Phương trình x²/5² + y²/7² = 1 có phải là phương trình chính tắc của elip không?

2. Cho E có tiêu điểm F₁(-2,0) đi qua điểm A (0,1), hãy lập phương trình chính tắc của Elip này.

Lời giải:

1. Theo định nghĩa đường chính tắc, ta có a > b > 0, tuy nhiên trong phương trình x²/5² + y²/7² = 1 , ta có b = 3, a = 7 mà 3 < 7 hay b < a.

Suy ra, phương trình x²/5² + y²/7² = 1 không phải là phương trình chính tắc của Elip.

2. Phương trình chính tắc của elip bất kỳ là x²/a² + y²/b² = 1, với a > b > 0

Ta có, F₁(-2,0) là một tiêu điểm của E nên c = 2.

Điểm A(0,2) ∈ (E) nên ta có phương trình 0²/a² + 2²/b² = 1 ⇔ 2²/b² = 1 ⇔ 2² = b² = 4

Với a² = b² + c² = 4 + 2² = 8

Vậy phương trình chính tắc cần tìm là: x²/8² + y²/4² = 1

Kiến thức 3 đường Conic - Đường hypebol

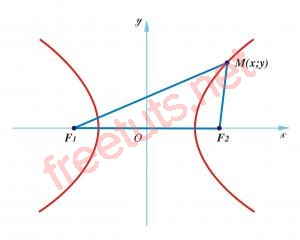
Hình Hypebol.

Khái niệm đường Hypebol

Cho hai điểm F₁ và F₂ cố định có khoảng cách F₁F₂ = 2c, với c > 0, đường Hypebol là tập hợp của các điểm M cùng nằm trên một mặt phẳng sao cho MF₁ - MF₂ = 2a, a là số nguyên dương cho trước, nhỏ hơn c, lúc này hai điểm F₁ và F₂ là hai tiêu điểm của đường Hypebol này.

Phương trình chính tắc của đường Hypebol

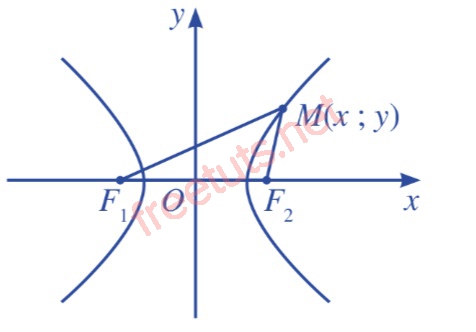
Hình ảnh minh họa về đường Hypebol.

Cho hệ trục tọa độ như hình trên, trục tung Ox đi qua 2 tiêu điểm F₁ và F₂ , trục hoành đi qua trung điểm của đoạn thẳng F₁F₂ = 2c, với c > 0, gốc O là trung điểm F₁F₂

Lúc này, ta sẽ có phương trình chính tắc của hypebol có dạng là

x2/a2 - y2/b2 = 1, với a > 0, b > 0, c2 = a2 + b2, 2c = F1F2.

Ví dụ minh họa:

Cho phương trình x²/4² - y²/6² = 1 có phải là phương trình chính tắc của hypebol không?

Lời giải:

Theo định nghĩa, phương trình chinh tắc của hypebol có dạng x²/a² - y²/b² = 1, với a > 0, b > 0

Xét phương trình x²/4² - y²/6² = 1, ta có a = 4, b = 6, a = 4 > 0 và 6 > 0

⟹ x²/4² - y²/6² = 1 là phương trình chính tắc của hypebol.

Kiến thức 3 đường Conic - Đường parabol

Khái niệm đường Parabol

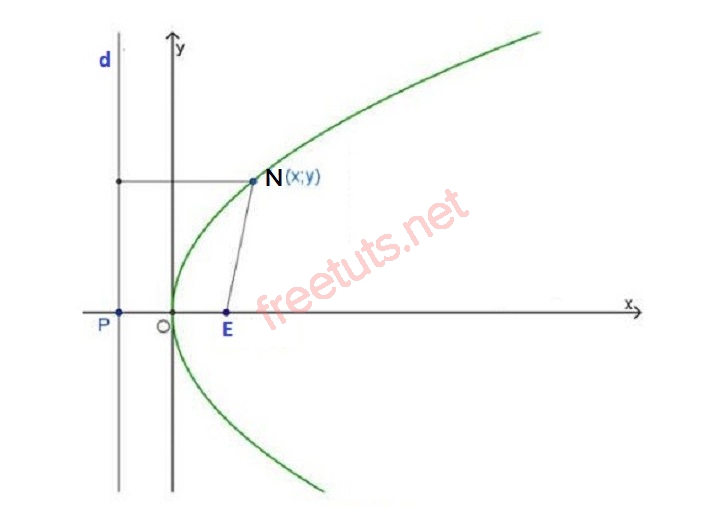
Hình ảnh minh họa về đường parabol.

Cho một điểm F cố định, và một đường thẳng Δ cố định không đi qua điểm F, đường Parabol là bao gồm tập hợp các điểm N nằm trong một mặt phẳng sao cho khoảng cách NF bằng khoảng các từ N đến đường thẳng Δ đã cho. Lúc này, F được gọi là tiêu điểm của parabol, đường thẳng Δ là đường chuẩn.

Phương trình đường chính tắc của đường Parabol

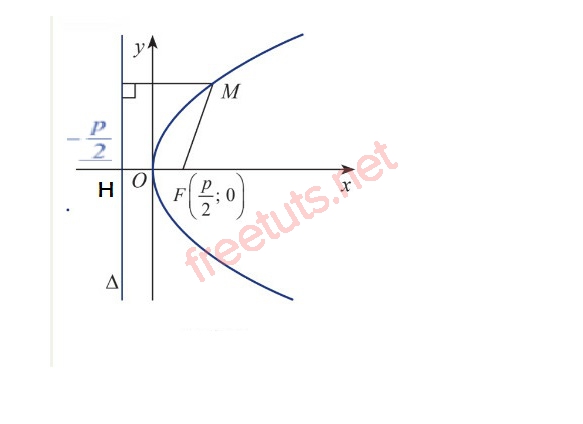
Phương trình chính tắc của đường Parabol.

Cho parabol P như hình trên, F là tiêu điểm, đường chuẩn Δ. Ta kẻ đường thẳng FH vuông góc với Δ , H là điểm nằm trên Δ , FH = p > 0.

Kẻ trục tọa độ Oxy, O là trung điểm của FH, Ox đi qua H, Oy là trục hoành.

Lúc này, ta sẽ có phương trình chính tắc của parabol là:

y2 = 2px, với p > 0. F(P/2;0) và x + (P/2) = 0.

Ví dụ minh họa:

Phương trình y² = -5x có phải là phương trình chính tắc của parabol không?

Lời giải:

Theo định nghĩa phương trình chinh tắc của parabol. ta có:

y² = -5x có dạng y² = 5px với p = -1 < 0.

Vậy phương trình y² = -5x không phải là pt chính tắc của parabol.

Các dạng bài tập về 3 đường Conic

Đối với 3 đường hypebol, elip, parabol chúng ta thường sẽ gặp hai dạng toán sau, mời các em cùng theo dõi các kiến thức mà freetuts đã tổng hợp bên dưới đây để nắm được cách giải nha:

Dạng 1: Xác định phương trình chính tắc

Đối với dạng toán này, các em cần nắm vững lý thuyết phương trình chính tắc của 3 đường conic elip, parabol, hypebol để có thể dễ dàng xác định được phương trình đã cho có phải là pt chính tắc không nhé.

Ví dụ: Phương trình y² = -6x có phải là phương trình chính tắc của Parabol không?

Lời giải:

Theo định nghĩa pt chính tắc của parapol có dạng y² = 2px, với p >0.

Ta có: y² = -6x ⇔ y² = 2.(-3)x, vậy p = -3 < 0, nên suy ra y² = -6x không phải là phương trình chính tắc của parabol.

Dạng 2: Viết phương trình chính tắc dựa vào tiêu điểm

Đối với dạng toán này, đề bài sẽ cho trước tiêu điểm của 3 đường conic, từ tọa độ của tiêu điểm, các em hãy xác định điểm a, b và sau đó dựa vào đó để viết ra được phương trình chính tắc.

Ví dụ:

Viết phương trình chinh tắc của đường Parabol (P), biết rằng (P) có tiêu điểm M(9,0).

Lời giải:

Ta có, phương trình chính tắc của (P) có dạng y² = 2px, với p >0.

Với (P) có tiêu điểm M(9,0), ta có p² = 9 => p = 3.

Vậy phương trình chính tắc của (P) là y² = 2.3.x = 6x.

Ứng dụng của 3 đường conic trong thực tế

Chiếc cầu có hình dạng parabol.

Hiện nay, trong thực tế có rát nhiều ứng dụng của 3 đường conic tồn tại xung quanh chúng ta, hãy cùng xem một số ứng dụng nổi bật sau nha:

• Ứng dụng đường parabol trong thiết kế đèn pha ô tô: Đèn pha ô tô thực chất là một chiếc gương cầu lõm có hình dạng parabol, bóng đèn sẽ được thiết kế đặt tại tiêu điểm của parabol. Khi ánh sáng phát ra từ bóng đèn sẽ chiếu lên bề mặt đèn pha, khi đó ánh sáng sẽ được tập trung và phản xạ thành các tia sáng song song, giúp chiếu sáng ở khoảng cách xa.

• Ứng dụng đường hypebol trong xây dựng cầu vòm: Trong cấu trúc cầu vòm, các đường cong hyberbol được sử dụng để thiết kế nhằm tạo ra các điểm chịu lực tối ưu và đảm bảo tính ổn định của công trình.

• Ứng dụng đường elip trong thiết kế quỹ đạo chuyển tiếp: Trong thám hiểm không gian, đường elip được sử dụng để thiết kế quỹ đạo chuyển tiếp, cho phép tàu vũ trụ di chuyển giữa các hành tinh một cách hiệu quả.

Bài tập 3 đường Conic

Sau khi đã nắm vững lý thuyết 3 đường conic rồi, bây giờ các em hãy vận dụng chúng để giải một số bài tập sau đây nha:

Bài 1: Cho hypebol (H), có tiêu điểm F(8,0) và (H) đi qua điểm A(5;0), viết pt chính tắc của (H).

Lời giải:

Ta biết, phương trình chính tắc của (H) có dạng:

x²/a² - y²/b² = 1, với a > 0, b > 0

Có điểm A(5;0) H, nên ta có x = 5, y = 5

5²/a² - 0²/b² = 1 ⇔ 5²/a² = 1 ⇔ 5² = a² ⟹ a = 5.

Do (H) có tiêu điểm M(8,0) nên c = 8.

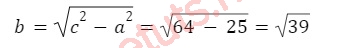
Vậy phương trình chính tắc của (H) là:

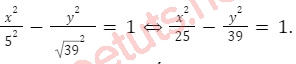
Bài 2: Phương trình nào sau đây là phương trình chính tắc của parabol?

1. y² = -2x
2. y² = -12x
3. y² = -8x
4. y² = 6x.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px, với p > 0.

• Đáp án A, có p = -1 < 0, sai.
• Đáp án B, có p = -4 < 0, sai.
• Đáp án C, có p = -8 < 0, sai.
• Đáp án D, có p = 3 > 0, đúng.

Vậy đáp án D. y² = 6x là đáp án đúng.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ các lý thuyết 3 đường conic, hy vọng đây sẽ là những thông tin hữu ích đối với các em học sinh. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi nhé!