Cách tìm tập nghiệm của bất phương trình bậc nhất, mũ và logarit

Cách tìm tập nghiệm của bất phương trình bậc nhất một ẩn, bậc hai một ẩn, bất phương trình tích, bất phương trình mũ, bpt logarit chi tiết tại đây.

Đối với chương trình toán đại số, tìm tập nghiệm của bất phương trình là một dạng bài tập vô cùng quan trọng và thường xuyên xuất hiện trong các bài kiểm tra. Tuy nhiên, chắc hẳn còn nhiều học sinh chưa nắm vững được các phương pháp để tìm tập nghiệm sao cho nhanh và chính xác nhất đúng không nào.

Các e đừng lo nha, vì trong bài viết hôm nay, freetuts sẽ hướng dẫn tất tần tật các cách tìm tập nghiệm bất phương trình nè, mời các em cùng theo dõi nha!

Tập nghiệm của bất phương trình là gì?

Tập nghiệm của bất phương trình là tập hợp tất cả các nghiệm của bất phương trình đó, hay còn gọi là miền đúng của bất phương trình.

Bài viết này được đăng tại [free tuts .net]

Ví dụ: Bất phương trình 2x + 2 > 0 có nghiệm đúng với mọi số thức x > -0.5. Vậy ta có tập nghiệm của bpt là {x ∈ R|x > -0.5} = (0.5;∞ ).

Cách tìm tập nghiệm của bất phương trình bậc nhất và bậc hai

Đối với mỗi loại bất phương trình khác nhau, chúng ta cũng sẽ có những phương pháp tìm tập nghiệm phù hợp. Hãy cùng theo dõi chi tiết ngay bên dưới đây nha.

Tìm tập nghiệm của bất phương trình lớp 8, bpt bậc nhất một ẩn

Đây là dạng bpt đơn giản nhất nên cách tìm nghiệm của bpt này cũng siêu dễ, các em hãy chú ý nha:

• Bước 1: Chuyển các hạng tử không chứa ẩn sang vế phải.

• Bước 2: Nhân hai vế của bpt với số nghịch đảo của hệ số của hạng tử có chứa ẩn.

• Bước 3: Giải bất phương trình như bình thường và tìm ra tập nghiệm của nó thôi nào.

Ví dụ: Giải bpt (2x + 3) > 0

Hướng dẫn giải:

Xét bpt (2x + 3) > 0 ⇔ 2x > -3(vì 3 không chứa ẩn nên ta chuyển 3 sang vế phải và đổi dấu thành -3).

⇔ 2x.1/2 > -3.(1/2x) > -3/2

Vậy tập nghiệm của bpt đã cho là {x|x > -3/2}.

Tìm tập nghiệm của bất phương trình bậc hai một ẩn

Đối với bpt bậc hai một ẩn, các em có thể áp dụng 2 phương pháp sau để giải một cách dễ dàng nè:

Phương pháp1: Dựa vào bảng xét dấu của tam thức bậc 2 tương ứng:

Cho bpt f(x) = ax2 + bx + c

Bước 1: Lập bảng xét dấu của bpt đã cho.

Bước 2: Dựa vào bảng xét dấu để tìm tập nghiệm bằng cách:

• Nếu f(x) > 0 thì chúng ta sẽ chọn những khoảng + là tập nghiệm.

• Nếu f(x) < 0 thì chúng ta sẽ chọn những khoảng - là tập nghiệm.

• Nếu a < f(x) < b thì chúng ta sẽ sử dụng dấu ngoặc tròn () để xác định các tập nghiệm.

• Nếu dấu của bpt f(x) là ≥ hoặc ≤ thì chúng ta sẽ dùng dấu ngoặc vuông [] để xác định tập nghiệm.

Ví dụ: Tìm tập nghiệm của bpt f(x) = x² + 3x + 2.

Lời giải: Giải bpt f(x) = x² + 3x + 2, có 2 nghiệm phân biệt là x_x = 1, x₂ = 2 , với a = 1 > 0, ta có bảng xét dấu:

Vậy tập nghiệm của bpt đã cho là (-∞,1) U (2,+)

Phương pháp 2: Sử dụng máy tính bỏ túi Casio để giải:

Có một cách nhanh hơn giúp các em có thể dễ dàng tìm được tập nghiệm bất phương trình bậc hai một ẩn đó chính là sử dụng máy tính Casio.

Để có thể tiến hành giải bpt, các em hãy chọn chức năng Inequality, sau đó nhấn phím số 2, nhập các hệ số của bất phương trình và nhấn phím =, lúc này chúng ta sẽ thu được tập nghiệm của bpt cần tìm. Qủa thật đơn giản đúng không nào.

Tìm tập nghiệm của bất phương trình tích

Đối với bất phương trình tích, các em hãy làm theo hướng dẫn sau của freetuts để có thể dễ dàng tìm được tập nghiệm của nó nha:

• Bước 1: Đặt vé trái của bpt đã cho là P(x)

• Bước 2: Phụ thuộc vào P(x) là nhị thức bậc 1 hay tam thức bậc 2 mà áp dụng định lý xét dấu phù hợp.

• Bước 3: Dựa vào bảng xét dấu ở trên, chúng ta sẽ tìm ra được tập nghiệm của bpt tích này.

Ví dụ: Hãy giải bpt (x - 2)(x + 3)(x - 5) > 0

Hướng dẫn giải:

Đặt P(x) = (x - 2)(x + 3)(x - 5) > 0

Với P(x) = 0(x - 2)(x + 3)(x - 5) = 0, ta có nghiệm là -3, 2, 5

Lập bảng xét dấu của P(x), ta có:

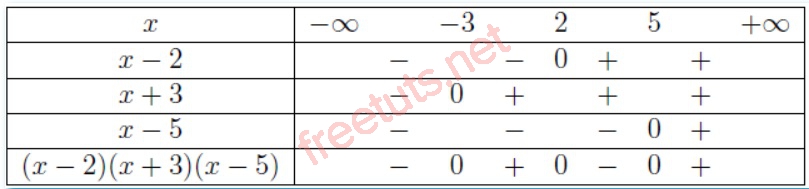
Vì đề bài cho P(x) > 0, nên những khoảng làm cho P(x) có giá trị dương là tập nghiệm của bpt đã cho.

Vậy tập nghiệm của bpt (x - 2)(x + 3)(x - 5) > 0 là (-3,2) U (5,+∞)

Cách tìm tập nghiệm của bất phương trình lớp 12, bất phương trình mũ

Đối với bất phương trình mũ, nếu bạn muốn tìm tập nghiệm của phương trình này, hãy áp dụng ngay 1 trong 4 phương pháp sau nha:

Phương pháp 1: Đưa về cùng cơ số

Tìm tập nghiệm của bpt mũ a^f(x) > a^g(x)

• Nếu a > 1 thì a^f(x) > a^g(x) ⇔ f(x) > g(x) (cùng chiều nếu a > 1).

• Nếu 0<a<1 thì a^f(x) < a^g(x) ⇔ f(x) < g(x) (ngược chiều khi 0 < a < 1)

• Nếu a chứa ẩn thì a^f(x) > a^g(x) Phương pháp 1: (a-1)[f(x) - g(x)] > 0

Phương pháp 2: Đặt ẩn phụ

Đối với phương pháp này, các em cần đặc biệt chú ý đến chiều biến thiên của hàm số nha.

Xét phương trình m.a^2f(x) + n.ab^f(x) + p.b^2f(x) > 0

• Chia cả 2 vế của bpt cho b^2f(x), ta có:

m.a^2f(x) + n.ab^f(x) + p.b^2f(x) > 0 ⇔ m.(a/b)^2f(x) + n.(a/b)^f(x)

• Đặt t = (a/b)^f(x), t > 0, ta có m.t² + n.t + p > 0

Phương pháp 3: Xét tính đơn điệu của hàm số

Cho hàm số y = f(t) xác định và liên tục trên D.

• Nếu hàm số f(t) đồng biến trên D và ∀u, v ∈ D thì f(u) > f(v) ⇔ u > v

• Nếu hàm số f(t) nghịch biến trên D và ∀u, v ∈ D thì f(u) > f(v) ⇔ u < v

Tìm tập nghiệm của bất phương trình logarit

Đây là một dạng toán khá khó vì có chứa logarit, tuy nhiên, các em đừng lo lắng, hãy áp dụng các bước sau để có thể tìm được tập nghiệm bất phương trình dạng này nha.

Phương pháp 1: Đưa về cùng cơ số:

Xét bất phương trình log_af(x) > log_ag(x) (a > 0, a ≠ 1)

• Nếu a > 1 thì log_af(x) > log_ag(x) ⇔ f(x) > g(x) (cùng chiều nếu a > 1).

• Nếu 0 < a < 1 thì log_af(x) >log_ag(x) ⇔ f(x) < g(x) (ngược chiều khi 0 < a < 1)

• Nếu a chứa ẩn thì log_af(x) > log_ag(x), khi f(x) > 0, g(x) > 0, (a - 1)[f(x) - g(x)] > 0

Phương pháp 2: Đặt ẩn phụ:

Nếu phương trình có dạng Q[log_af(x)] > 0, các em có thể đặt ẩn phụ t = log_af(x) và sau đó tiến hành giải như bình thường thôi nè.

Bài tập tìm tập nghiệm của bất phương trình

Như vậy, qua những chia sẻ trên, các em đã nắm vững các phương pháp tìm tập nghiệm của bpt rồi đúng không nào, bây giờ hãy áp dụng chúng để giải một số bài tập dưới đây để rèn luyện thêm nha.

Bài 1: Tìm nghiệm của bất phương trình (x - 1)² > x.(x + 3)

Lời giải:

xét bpt: (x - 1)² > x.(x + 3)

⇔ x² - 2x + 1 > x² + 3x

⇔ 1 > x² + 3x - x² + 2x

⇔ 1 > 5.x ⇔ x < 1/5.

Bài 2: Giải bpt sau 2x³ - 3x² - 3x + 2 ≤ 0

Lời giải:

Xét bpt 2x³ - 3x² - 3x + 2 ≤ 0

(x + 1).(2x² - 5x + 2) ≤ 0

(x + 1)(x + 2)(2x - 1) ≤ 0

Ta có bảng xét dấu sau:

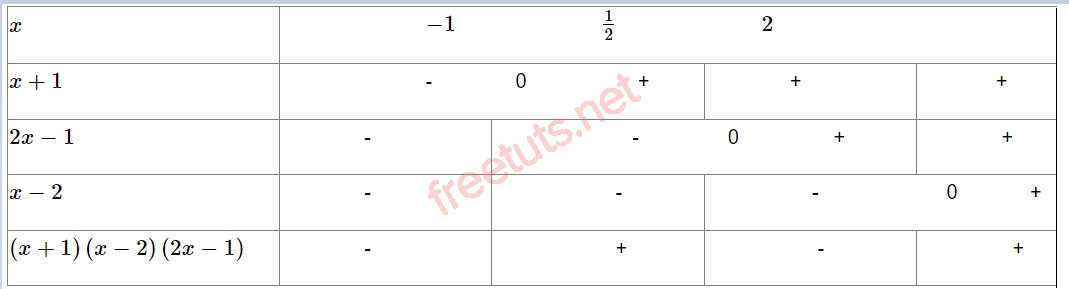
Vậy tập nghiệm của bpt là x ≤ -1và 1/2 ≤ x ≤ 2.

Bài 3: Tìm tập nghiệm của các bpt sau:

1. (x² - 9x + 14)/(x² - 5x + 4) > 0

2. log₂(x² + 3x) > 2

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ phương pháp tìm tập nghiệm của bất phương trình bậc nhất, mũ và logarit, hy vọng các em có thể áp dụng thành công những kiến thức này để có kết quả tốt hơn trong học tập nha.