Tổng hợp công thức lượng giác 9, 10, 11, 12 đầy đủ và chuẩn nhất

Bảng hệ thống công thức lượng giác lớp 9, 10, 11 và 12 đầy đủ từ cơ bản đến nâng cao và một số dạng bài tập liên quan thường gặp cùng cách giải chi tiết.

Trong bộ môn toán học, công thức lượng giác là một trong những nội dung vô cùng quan trọng mà bắt buộc các em học sinh lớp 9, 10,11 và 12 phải thuộc làu để có thể dễ dàng giải quyết các bài tập liên quan. Trong bài viết hôm nay, hãy cùng freetuts ôn tập lại các ct lượng giác quan trọng và một số dạng bài tập phổ biến nha.

Công thức lượng giác lớp 9

Ngay bên dưới đây là những kiến thức quan trọng về các công thức lượng giác cũng như hệ thức lượng trong tam giác vuông mà các học sinh lớp 9 cần nắm vững để có thể giải các bài tập liên quan và làm nền móng để có thể tiếp thu được các kiến thức toán học lượng giác trong chương trình THPT.

Công thức lượng giác cơ bản lớp 9

Tỉ số lượng giác của một số góc đặc biệt

• Cho 2 góc α, β với α + β = 90 độ, ta có:

sin α = cos β; cos α = sin β
tan α = cot β; cot α = tan β

• Nếu sin α = sin β ⟹ α = β

  Bài viết này được đăng tại [free tuts .net]

• Cho góc nhọn α bất kỳ, với điều kiện 0 < sin α < 1, 0 < cos α < 1, 0 < tan α < 1, 0 < cot α < 1, ta có:

tan α = sin α / cos α
cot α = cos α / sin α
tan α x cot α =1 

Công thức lượng giác quan trọng lớp 10, 11, 12

Cùng tìm hiểu những ct lượng giác quan trọng trong chương trình toán 10, 11 và 12 ngay bên dưới đây nhé.

Công thức lượng giác cơ bản

Công thức cộng lượng giác

Công thức các cung liên kết

Đối với các cung liên kết trên một đường tròn lượng giác, các em hãy lưu ý một số công thức sin cos tan quan trọng sau nha:

Trường hợp 1: Hai góc đối nhau

cos(-x) = cosx
sin(-x) = -sinx
tan(-x) = -tanx
cot(-x) = -cotx

Trường hợp 2: Hai góc kề bù

sin(π - x) = sinx
cos(π - x) = sinx
tan(π - x) = -tanx
cot(π - x) = -cotx

Trường hợp 3: hai góc phụ nhau

sin(π/2 - x) = cosx
cos(π/2  - x) = sinx
tan(π/2 - x) = cotx
cot(π/2  - x) = tanx

Trường hợp 4: Hai góc hơn kém nhau π, π/2

sin(π + x) = -sinx
cos(π + x) = -cosx
tan(π + x) = tanx
cot(π + x) = cotx
sin(π/2 + x) = cosx
cos(π/2 + x) = -sinx
tan(π/2 + x) = -cotx
cot(π/2 + x) = -tanx

Công thức nhân lượng giác

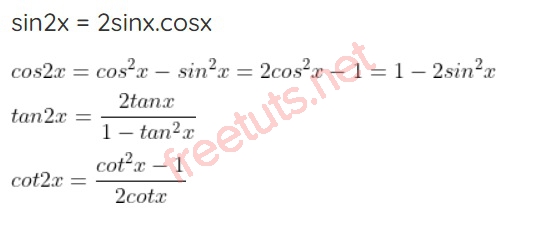
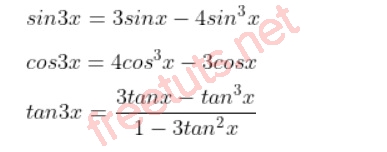
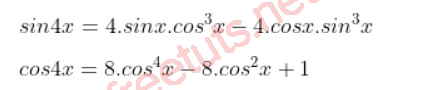
Công thức lượng giác hạ bậc

Nếu muốn hạ bậc một hàm lượng giác, các em hãy nắm vững công thức hạ bậc lượng giác ngay bên dưới đây nha:

Công thức lượng giác tích thành tổng

Để tính tích 2 hàm lượng giác, các em hãy lưu ý các công thức biến đổi tích thành tổng dưới đây nha.

Công thức lượng giác hiệu thành tích, tổng thành tích

Nếu gặp các phép toán cộng, trừ lượng hàm lượng giác, hãy áp dụng các công thức trong bảng lượng giác dưới đây nha.

Công thức nghiệm của pt lượng giác

Công thức nghiệm cơ bản:

Nghiệm của một số trường hợp đặc biệt

Công thức lượng giác nâng cao

Ngoài các ct lượng giác cơ bản ở trên, các em cũng nên lưu ý một số công thức lượng giác đặc biệt ngay bên dưới đây, để có thể linh hoạt trong việc giải bài tập liên quan nha.

Bảng lượng giác cơ bản của các góc đặc biệt

Để giúp quá trình tính toán được diễn ra nhanh hơn, các em hãy ghi nhớ một số giá trị lượng giác của các góc đặc biệt mà freetuts đã tổng hợp ngay bên dưới đây nha.

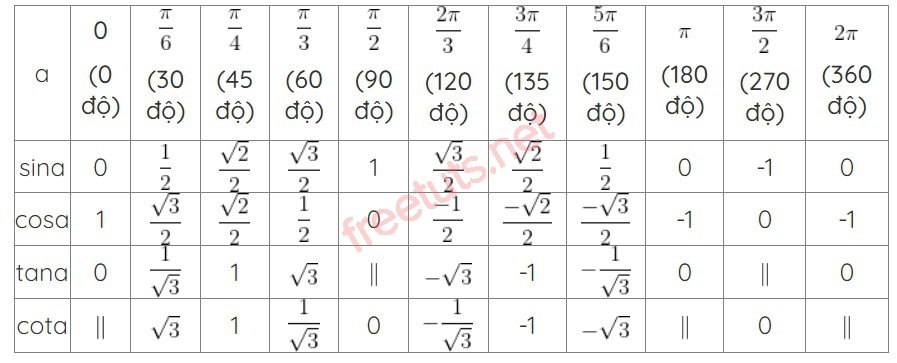
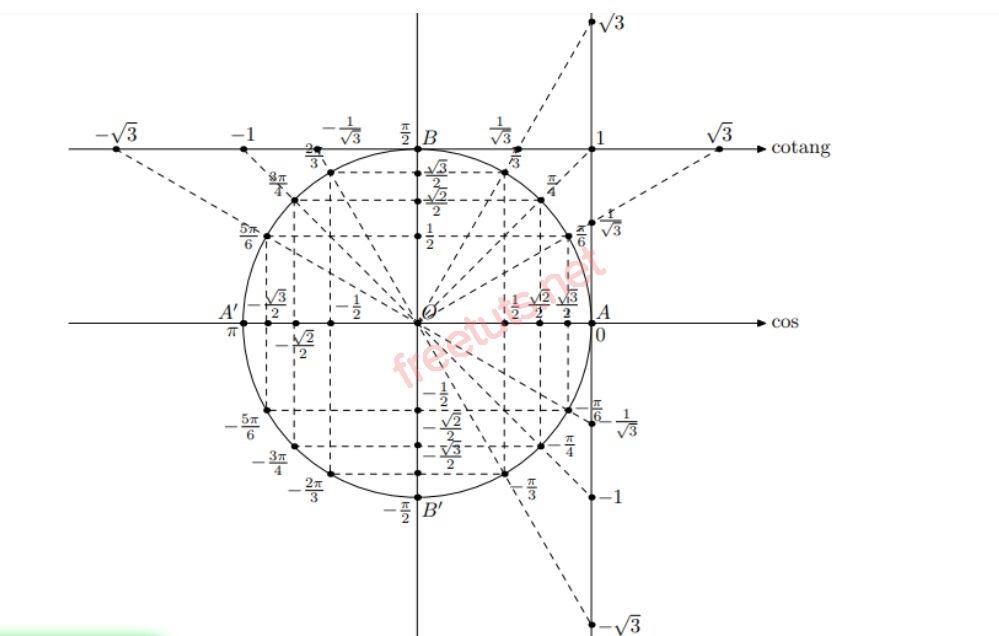
Số đo các góc đặc biệt biểu thị trên trục.

Xem thêm: Công thức đạo hàm lớp 11, 12 từ cơ bản đến cao cấp

Các dạng bài tập liên quan đến công thức lượng giác

Trong toán học, đối với hàm lượng giác sẽ có một số dạng bài tập căn bản sau, mời các em cùng tìm hiểu để biết được hướng giải quyết đúng nha.

Dạng 1: Tính giá trị lượng giác của một góc bất kỳ

Đối với dạng bài tập này, các em cần kết hợp các kiến thức như: bảng giá trị lượng giác đặc biệt cùng các ct lượng giác đã nên ở trên để có thể dễ dàng giải quyết bài toán này nha.

Ví dụ minh họa: cos(37π)/12 = ?

Lời giải:

Có: cos(37π)/12 = cos(2π + π + π/12) = cos(π + π/12)

= -cos(π/12) = -cos(π/3 - π/4) = -cos(π/3).cos(π/4) + sin(π/3).sin(π/4)

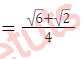
Dạng 2: Rút gọn biểu thức lượng giác

Đây là một dạng bài tập khá là phổ biến trong toán học, khi gặp các dạng bài này, các em hãy áp dụng các ct lượng giác đã nêu ở trên để có thể biến đổi biểu thức phức tạp ban đầu về dạng biểu thức đơn giản, ngắn gọn nhất có thể nha.

Ví dụ minh họa:

Rút gọn biểu thức lượng giác sau: A = cos10x + 2cos²4x + 6coss3x.cosx - cosx - 8cosx.cos³3x

Lời giải:

A = cos10x + 2cos²4x + 6coss3x.cosx - cosx - 8cosx.cos³3x

= cos10x + (1 + cos8x) - cosx - 2(4cos³3x - 3cos3x)cosx

=(cos10x + cos8x) + 1 - cosx - 2cos9x.cosx

=2cos9x.cosx + 1- cosx - 2cos9x.cosx = 1 - cosx.

Dạng 3: Chứng minh hai đẳng thức lượng giác bằng nhau

Để giải dạng bài tập dạng này, bạn hãy áp dụng một trong các phương pháp sau nha.

• Phương pháp 1: Áp dụng các ct lượng giác để biến đổi một vế thành vế còn lại.

• Phương pháp 2: Biến đổi 2 đẳng thức lượng giác đã cho về một đẳng thức đã biết.

Ví dụ: Chứng minh đẳng thức sau:

sin⁴x + cos⁴x = 1/4.cos4x + 3/4

Lời giải:

Áp dụng công thức hạ bậc, ta có:

sin⁴x + cos⁴x = (sin²x + cos²x)² - 2sin²x.cos²x

= 1 - 1/2.sin²2x = 1 - 1/2.(1 - cos4x)/2 = 3/4 + 1/4.cos4x.

Dạng 4: Chứng minh biểu thức lượng giác không phụ thuộc vào biến x

Đây cũng là một dạng bài tập khá là thú vị trong toán lớp 11, nếu gặp dạng bài tập này, các em chỉ cần sử dụng các công thức sin cos tan đã học để rút gọn biểu thức sao cho mất biến x đi, vậy là ta đã chứng minh được rồi nè.

Ví dụ:

Chứng minh biểu thức sau không phụ thuộc vào biến x:

B = cos²x + cos²(π/3 + x) + cos²(3 - x)

Lời giải: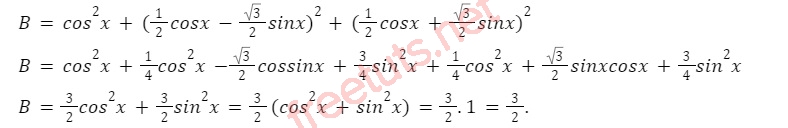

Như vậy, ta có thể kết luận biểu thức B không phụ thuộc vào x.

Bài tập áp dụng công thức lượng giác

Sau khi đã nắm vững các ct lượng giác ở trên, bây giờ các em hãy vận dụng chúng để giải nhanh các bài tập dưới đây nha.

Bài 1: Công thức lượng giác lớp 10:

Cho x + y + z = π, hãy chứng minh biểu thức sau là đúng:

tanx + tany + tanz = tanx.tany.tanz.

Lời giải:

Với x + y + z = x + y = -z

tan(x + y) = tan(π - z)

⇔ (tanx + tany)/(1 - tanx.tany) = -tanz ⇔ tanx + tany = -tanz + tanx.tany.tanz

⇔ tanx + tany + tanz = tanx.tany.tanz

Bài 2: Công thức lượng giác lớp 9, tính giá trị biểu thức sau:

A = cos(-53).sin(-337) + sin307.sin113

Lời giải:

Có A = cos(-53).sin(-337) + sin307.sin113

⇔ A = cos(-53).sin(23-360) + sin(-53 + 360).sin(90 + 23)

⇔ A = cos(-53).sin23 + sin(-53).cos23 = sin(23 - 53) = -sin30 = -12

Bài 3: Rút gọn biểu thức sau:

M = (cosa + 2cos3a + cos5a)/(sina + 2sin3a + sin5a)

Lời giải:

M =(cosa + 2cos3a + cos5a)/(sina + 2sin3a + sin5a) = (2coss3a.cos2a + 2cos3a)/(2sin3acos2a + 2sin3a) = (2cos3a(cos2a + 1))/(2sin3a(cos2a + 1)) = (cos3a)/(sin3a) = cot3a

Mẹo học thuộc bảng công thức lượng giác siêu nhanh

Sau đây là một số tips nhỏ giúp các em dễ dàng ghi nhớ được các ct lượng giác quan trọng nè.

Áp dụng các công thức vào các bài tập

Một trong những cách tốt nhất để học thuộc các ct lượng giác là áp dụng các công thức này vào các bài tập. Bằng cách giải quyết các bài tập, các em sẽ có thể củng cố kiến thức của mình về các công thức và hiểu rõ hơn cách sử dụng chúng, qua đó giúp ghi nhớ được lâu hơn.

Học thuộc thông qua các bài thơ về ct lượng giác

Hiện nay, có rất nhiều bài thơ hay về công thức lượng giác 11, mời các em cùng tham khảo:

• Cos đối, sin bù, phụ chéo, tan hơn kém .

• Sin thì sin cos, cos sin/ cos thì cos cos, sin sin rồi trừ/ Tang tổng thì bằng tổng tang/ Chia 1 trừ với tích tang dễ mà.

• tang mình cộng với tang ta, bằng sin 2 đứa trên cos ta cos mình.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ tất tần tật các công thức lượng giác lớp 9, 10 và 11 từ cơ bản đến nâng cao, hy vọng đây sẽ là những thông tin hữu ích đối với các em học sinh. Hẹn gặp lại các em trong những bài viết tiếp theo để cùng nhau tìm hiểu về các kiến thức môn học khác nữa nhé.