Tổng hợp các tác giả văn học hiện đại Việt Nam 
Số tự nhiên là gì? Sự khác nhau giữa tập hợp N và N* 
Tiểu sử nhà văn Tô Hoài: Sự nghiệp sáng tác văn học của ông 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Cách tính delta, delta phẩy và một số bài tập áp dụng
Cách tính delta và delta phẩy trong phương trình bậc 2 để biết được số nghiệm của phương trình, delta Δ = b^2 - 4ac và delta phẩy Δ’ = b’^2 - ac.
Để tìm được nghiệm của các phương trình bậc 2 thì cách tính delta và delta phẩy là bước đầu tiên đóng vai trò quan trọng giúp các em xác định được số nghiệm của phương trình, từ đó không bị bỏ sót nghiệm. Trong bài viết hôm nay, hãy cũng freetuts ôn tập lại cách tính delta phẩy và delta của một phương trình bậc 2 bất kỳ và áp dụng để giải một số bài tập liên quan nha.
Hiểu về delta và delta phẩy trong toán học
Delta và delta phẩy sẽ cho chúng ta thông tin về số nghiệm của phương trình bậc hai dựa vào dữ liệu sau:
- Nếu Δ, Δ’ > 0, phương trình bậc 2 có 2 nghiệm phân biệt
- Nếu Δ, Δ’ < 0, phương trình bậc 2 này không có nghiệm thực.
- Nếu Δ, Δ’ = 0, phương trình bậc 2 này có một nghiệm kép.
Chính vì vậy, nếu nắm vững được cách tính delta và delta phẩy sẽ giúp các em giải các bài toán liên quan đến phương trình bậc hai một cách nhanh và chính xác nhất.
Bài viết này được đăng tại [free tuts .net]
Cụ thể như sau:
Cho phương trình bậc hai một ẩn như sau:
ax^2 + bx + c = 0, với a, b là hệ số, c là hằng số, a ≠ 0, ta lần lượt có các cách tính nghiệm của phương trình như sau:
Với Δ = b^2 - 4ac
-
Nếu Δ > 0, phương trình ax^2 + bx + c = 0 sẽ có hai nghiệm phân biệt là:
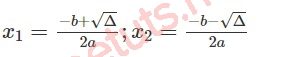
- Nếu Δ < 0, phương trình ax^2 + bx + c = 0 vô nghiệm.
- Nếu Δ = 0, phương trình ax^2 + bx + c = 0 sẽ có nghiệm kép là: x1 = x2 = (-b/2a)
Với Δ’ = b’^2 - ac, b’ = b/2, ta có:
-
Nếu Δ’ > 0, phương trình ax^2 + bx + c = 0 sẽ có hai nghiệm phân biệt là:
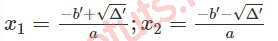
- Nếu Δ’ < 0, phương trình ax^2 + bx + c = 0 vô nghiệm.
- Nếu Δ’ = 0, phương trình ax^2 + bx + c = 0 sẽ có nghiệm kép là: x1 = x2 = (-b/a)
Cách tính delta và delta phẩy trong phương trình bậc 2
Trong phương trình bậc 2, delta (denta) và delta phẩy (denta phẩy) lần lượt có ký hiệu là Δ, Δ’ được dùng để biểu thị biệt thức của phương trình bậc 2.
Biệt thức delta này được tính bằng công thức:
Δ = b^2 - 4ac
Công thức tính delta phẩy như sau:
Δ’ = b’^2 - ac, b’ = b/2
Trong đó:
a, b và c lần lượt là các hệ số trong phương trình ax^2 + bx + c = 0.
delta phẩy được ký hiệu là Δ’
Ví dụ minh họa: Cho phương trình bậc 2: 2x^2 + 4x + 1 = 0.
Vậy Δ = 4^2 - 4.2.1 = 16 - 8 = 8
Vậy Δ’ = (4/2)^2 - 2.1 = 2
Bài tập tính delta phẩy và delta phương trình bậc 2
Như vậy, các em đã nắm được cách tính delta và delta phẩy rồi đúng không nào. Bây giờ hãy áp dụng công thức tính delta phẩy và delta để đi giải một số bài tập sau nha.
Bài 1: Hãy giải các phương trình sau:
- x^2 - 6x + 3 = 0.
- 8x^2 + x + 2 = 0.
Lời giải:
a. x^2 - 6x + 3 = 0
Ta có Δ’ = b’^2 - ac = 3^2 - 1.3 = 6 > 0, nên phương trinh đã cho có 2 nghiệm phân biệt là:
x1 = (-(b’) + √(Δ’))/a = -(-6/2) + √6/1 = 3 + √6
x2 = (-(b’) - √(Δ’))/a = -(-6/2) - √6/1 = 3 - √6
Vậy phương trình đã cho có tập nghiệm là S = {3 - √6; 3 + √6 }
b. 8x^2 + x + 2 = 0
Ta có Δ = b^2 - 4ac = 1^2 - 4.8.2 = -63 < 0
Vậy phương trình đã cho vô nghiệm.
Bài 2: Cho phương trình x^2 - 3x + n^2 - 2n = 0 (1)
a. Tìm n để phương trình có nghiệm bằng 1
b. Tìm n để phương trình có nghiệm kép
Lời giải:
a. Vì x = 1 là nghiệm của phương trình nên thế x = 1 vào ta có:
1^2 - 3.1 + n^2 - 2n = 0 ⇔ - 2 + n^2 - 2n = 0 ⇔ n^2 - 2n - 2 = 0 (2)
Xét phương trình (1), ta có:
Δ’ = b’^2 - ac = (-1)^2 - 1.(-2) = 3 > 0
Vậy phương trình (1) có 2 nghiệm phân biệt là:
n1 = (-(b’) + √(Δ’))/a = -2/2 + √3/1 = √3 - 1
n2 = (-(b’) - √(Δ’))/a = -2/2 - √3/1 = -1 - √3
Vậy vói n = √3 - 1 hoặc n = -1 - √3 thì x = 1 là nghiệm của phương trình (1)
b. Xét phương trình (1), ta có:
Δ = b^2 - 4ac = (-3)^2 - 4.1.(n^2 - 2n) = 9 - 4n^2 - 8n = -4n^2 - 8n + 9 (3)
Để phương trình có nghiệm kép thì Δ = 0
⇔ -4n^2 - 8n + 9 = 0 (4)
giải hệ phương trình (4), ta có:
Δ’4 = b’^2 - ac = (-4)^2 - (-4).9 = 16 + 36 = 52 > 0, vậy phương trình (4) có 2 nghiệm phân biệt là:
n1 = (-(b’) + √(Δ’))/a = -8/2 + √52/(-4) = -4 - √52/4
n2 = (-(b’) - √(Δ’))/a = -8/2 - √52/(-4) = √52/4 - 4
Vậy với n = √52/4 - 4 hoặc n = -4 - √52/4 thì phương trình (1) có nghiệm kép.
Bài 3: Xác định a, b’, c và giải các phương trình sau.
a. 4x^2 + 8x + 1 = 0
b. 2024x^2 - 16x + 1 = 0
Lời giải:
a. 4x^2 + 8x + 4 = 0
Ta có a = 4, b’ = 4, c = 1
Suy ra Δ’ = 4^2 - 4.4 = 0
Vậy phương trình có nghiệm kép:
x1 = x2 = -4/4 = -1.
b. 2024x^2 - 16x + 1 = 0
Ta có a = 2024, b’ = -8, c = 1
Suy ra Δ’ = (-8)^2 - 2024.1 = -1960 < 0, vậy phương trình đã cho vô nghiệm.
Hỏi đáp liên quan đến delta và delta phẩy?
Khi nào dùng delta phẩy?
Thông thường, khi phương trình bậc 2 có hệ số b là số chẵn thì chúng ta sẽ sử dụng delta phẩy.
Khi nào dùng delta?
Delta sẽ dùng cho mọi trường hợp tính toán, kể cả b có là số chẵn hay số lẻ thì chúng ta để sử dụng denta được.
Như vậy, trên đây freetuts.net đã chia sẻ các kiến thức liên quan đến cách tính delta và delta phẩy phương trình bậc 2, các em hãy luyện tập thật kỹ để có thể tự tin giải các bài toán liên quan nha. Nếu muốn xem thêm nhiều tài liệu tham khảo về môn toán thì hãy ghé ngay trang web của chúng tôi nha.
