Cách tính khoảng cách giữa 2 đường thẳng đầy đủ các dạng

Khoảng cách giữa 2 đường thẳng chéo nhau trong không gian chính bằng độ dài của đoạn thẳng vuông góc chung với hai đường thẳng ấy.

Khoảng cách giữa 2 đường thẳng chéo nhau là một kiến thức rất quan trọng và phổ biến trong chương trình toán lớp 11. Tuy nhiên các em đã nắm vững được các cách tính khoảng cách giữa hai đường thẳng chưa nào? Nếu chưa thì hãy cùng tham khảo ngay bài viết dưới đây của freetuts để được hướng dẫn cụ thể nha.

Khoảng cách giữa 2 đường thẳng là gì?

Chúng ta có thể hiểu khoảng cách giữa hai đường thẳng theo những khái niệm sau:

• Khoảng cách giữa 2 đường thẳng trong không gian chính bằng độ dài đoạn vuông góc chung của 2 đường thẳng này

• Đoạn vuông góc chung chính là đoạn thẳng nối 2 điểm trên 2 đường thẳng và vuông góc với 2 đường thẳng này.

Ví dụ minh họa:

Bài viết này được đăng tại [free tuts .net]

Cho 2 đường thẳng a và b bất kỳ, trong đó, M thuộc a, N thuộc b, MN vuông góc với a, MN Vuông góc với b, vậy MN chính là đoạn vuông góc chung của đường thẳng a và b, suy ra khoảng cách giữa a và b chính bằng MN.

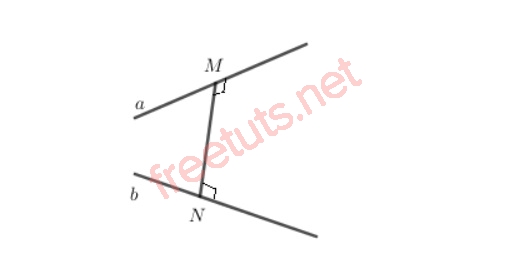
Hình ảnh minh họa khoảng cách giữa hai đường thẳng a và b.

Lưu ý: Giữa 2 đường thẳng chéo nhau, chỉ tồn tại duy nhất môt đoạn vuông góc chung.

• Khoảng cách giữa hai đường thẳng chéo nhau cũng chính là khoảng cách giữa 1 đường thẳng đến mặt phẳng song song chứa đường thẳng còn lại.

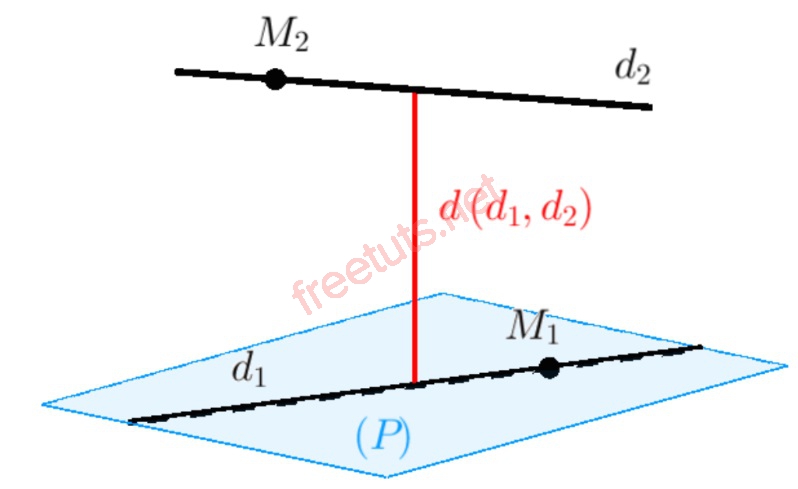
Mặt phẳng (P) chứa đường thẳng d1, song song với d2.

Ví dụ minh họa:

Cho 2 đường thẳng d1, d2 chéo nhau, d1 thuộc mặt phẳng (P), d2 song song với (P), tính khoảng cách giữa 2 đường thẳng d1;d2.

Dựa vào định nghĩa, ta có khoảng cách giữa d1 và d2 chính bằng khoảng cách từ d2 đến mặt phẳng (P).

Khoảng cách giữa hai đường thẳng chéo nhau chính bằng khoảng cách giữa 2 mặt phẳng song song chứa 2 đường thẳng đó.

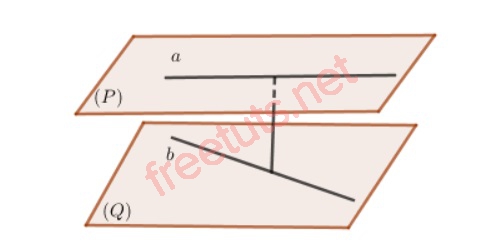
Hình ảnh về 2 mặt phẳng song song và chứa 2 đường thằng a. b

Ví dụ minh họa:

Cho 2 đường thẳng a, b bất kỳ trong không gian, a thuộc mặt phẳng (P), b thuộc mặt phẳng (Q), (P) song song với (Q). Khoảng cách giữa a và b chính bằng khoảng cách giữa hai mặt phẳng (P) và (Q).

Cách tính khoảng cách giữa 2 đường thẳng chéo nhau

Dựa vào khái niệm khoảng cách giữa hai đường thẳng chéo nhau, chúng ta cũng có các cách tính khoảng cách như sau:

Cách 1: Tính độ dài đoạn vuông góc chung giữa 2 đường thẳng

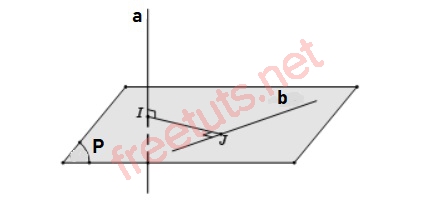
Cho hai đường thẳng a, b vừa chéo nhau, vừa vuông góc với nhau. Lúc này, để tính khoảng cách giữa a và b, ta làm như sau:

• Bước 1: Dựng mặt phẳng (P) chứa b và (P) vuông góc với a tại điểm I.
• Bước 2: Kẻ đường thẳng IJ vuông góc với b, IJ thuộc (P).
• Bước 3: Lúc này, khoảng cách giữa a và b chính bằng đoạn IJ.

Ví dụ minh họa:

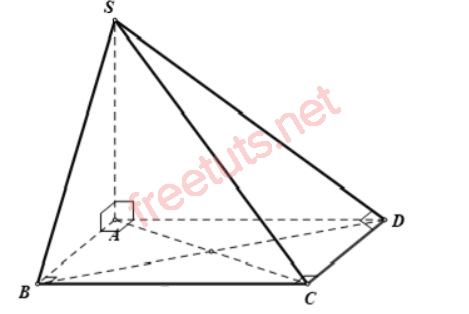
Cho hình chóp S.ABCD, ABCD là hình chữ nhật, SA vuông góc với (ABCD), AC = 5, BC = AD = 3. Tính khoảng cách giữa 2 đường thẳng SD và BC.

Lời giải:

Vì ABCD là hình chữ nhật nên ta có DC vuông góc với AD (1)

SA vuông góc với (ABCD) nên SA vuông góc với DC (2)

AD, SA thuộc mặt phẳng (SAD) (3)

Kết hợp (1), (2), (3), ta có DC vuông góc với (SAD) và DC vuông góc với SD.

Mà ta có DC vuông góc với BC, nên suy ra:

DC là đoạn vuông góc chung giữa SD và BC, vậy khoảng cách giữa SD và BC chính bằng đoạn DC.

Xét tam giác vuông ACD, áp dụng định lý Pytago, ta có:

DC^2 = AC^2 - AD^2 = 5^2 - 3^2 = 16, vậy DC = 4.

Suy ra khoảng cách giữa SD và BC là 4.

Cách 2: Tính khoảng cách từ đường thẳng tới mặt phẳng song song và chứa đường thẳng còn lại

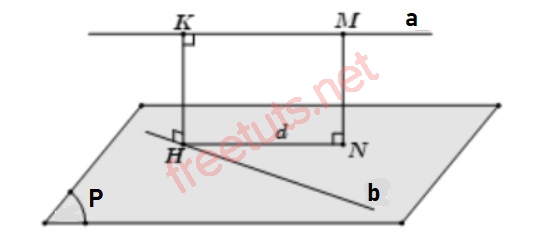
Hình ảnh minh họa.

Cho hai đường thẳng a, b chéo nhau, a,b không vuông góc với nhau, lúc này để tính khoảng cách giữa hai đường thẳng a và b, ta làm theo các bước sau:

• Bước 1: Chọn mặt phẳng (P) chứa và (P) song song với a.
• Bước 2: Chọn M thuộc a, N thuộc (P), sao cho MN vuông góc với (P).
• Bước 3: Kẻ d đi qua N và d song song với a, d cắt b tại H, lấy K thuộc a và HK vuông góc với a.
• Bước 4: Lúc này ta có HK là đoạn vuông góc chung của a và b, Và khoảng cách giữa a và b chính bằng HK.

Ví dụ minh họa: Cho hình chóp S.ABCD, ABCD là hình vuông, có cạnh bằng 4, SA = 4, SA vuông góc với (ABCD), tính khoảng cách giữa 2 đường thẳng trong hình chóp là AB và SC.

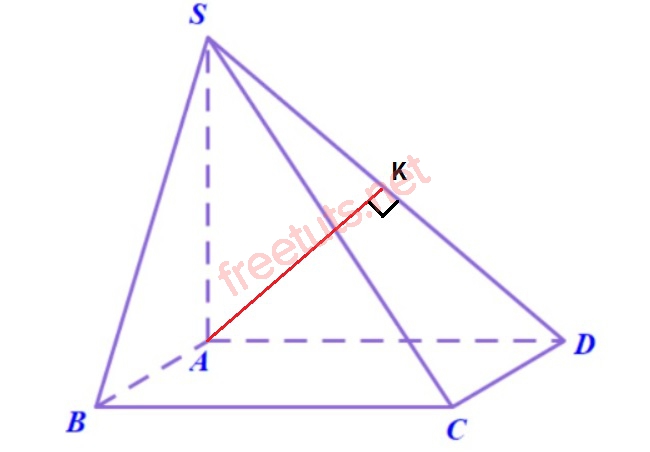
Lời giải:

Vì ABCD là hình vuông, nên ta có AB song song với CD, suy ra AB song song với mặt phẳng (SCD).

Vậy khoảng cách giữa 2 đường thẳng AB với SC chính bằng khoảng cách giữa AB và mặt phẳng (SCD).

d(AB, SC) = d(AB, (SCD)).

Từ điểm A, kẻ đường thẳng AK vuông góc với với SD, AK thuộc SAD.

Vì SA = AD = 4, nên tam giác SAD là tam giác cân, suy ra:

AK = 1/2.SD nhân căn 2 = 2 căn 2.

Vậy d(AB, SC) = d(AB, (SCD)) = 2 căn 2.

Cách 3: Tính khoảng cách giữa hai mặt phẳng song song chứa 2 đường thẳng

Có một cách khác giúp bạn có thể tính khoảng cách giữa hai đường thẳng chéo nhau mà freetuts sẽ giới thiệu cho các bạn đó chính là tính khoảng cách giữa 2 mặt phẳng song song chứa 2 đường thẳng đã cho.

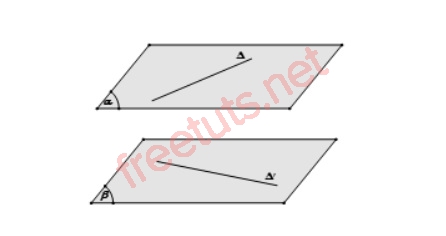
Cho hai đường thằng a, b chéo nhau, để tính khoảng cách giữa a và b, chúng ta làm như sau:

• Bước 1: Dựng mặt phẳng (P) sao cho (P) chứa a
• Bước 2: Dựng mặt phẳng (Q), sao cho (Q) chứa b và (Q) song song với (P).
• Bước 3: Lúc này ta có, d(a,b) = d ((P), (Q)).
• Bước 4: Hãy áp dụng các định lý, tính chất trong tam giác để tìm được khoảng cách giữa hai mặt phẳng (P) và (Q) nhé.

Ví dụ minh họa:

Cho hình hộp đứng ABCD.A’B’C’D’, (A’B’C’D’) là hình bình hành, AD = 6, AB = 3, góc BAD = 60 độ, AA’ = 4. M, N, P lần lượt là trung điểm của A’B’, BD, DD’. BH vuông góc với AD, H thuộc AD. Tính khoảng cách giữa MN và HP.

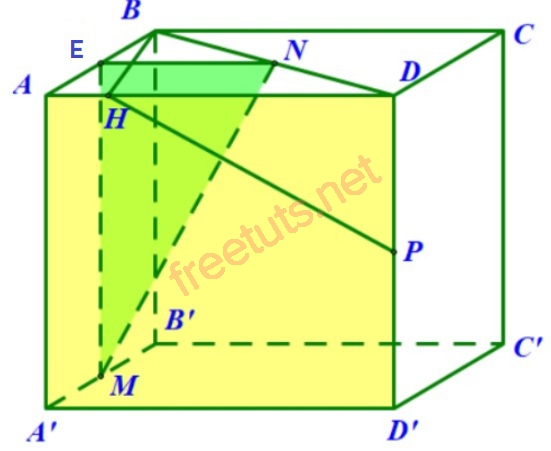
Lời giải:

Gọi E là trung điểm của AB, ta có (MNE) song song với (ADD’A’), MN thuộc (MNQ), HP thuộc (ADD’A’), nên ta có:

d(MN, HP) = d((MNE), (ADD’A’)) = d(E, (ADD’A’)) = 1/2 d(B,(ADD’A’) = 2, (vì E là trung điểm của AB)

Cách 4: Sử dụng phương pháp tích hai véc tơ

Cách tính khoảng cách hai đường thẳng chéo nhau Oxyz như sau:

Nếu MN là đoạn vuông góc chung của AB và CD, ta có:

Nếu trong mặt phẳng an pha, có 2 véc tơ không cùng phương là u1 và u2 thì ta có công thức sau:

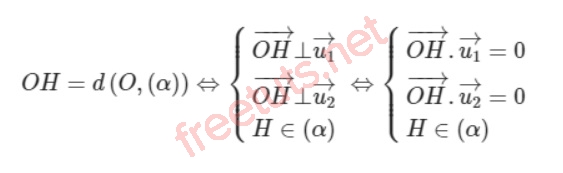
Ví dụ minh họa:

Cho hai đường thẳng a = 3x - 8y - 101 = 0, và b = 3x - 4y =0. Tính khoảng cách giữa d và d’.

Lời giải:

Xét 2 đường thẳng a và b, ta có:

3/6 = -4/(-8) và khác 0/(-101), nên suy ra hai đường thẳng a và b song song với nhau.

Trên đường thẳng a, lấy điểm O(0, 0).

Vì a // b nên d(a, b) = d(O, b) và bằng:

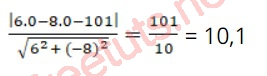
Vậy khoảng cách giữa hai đường thẳng a, b là 10,1.

Bài tập tính khoảng cách giữa 2 đường thẳng

Như vậy, tới đây, các em đã nắm được cách tính khoảng cách giữa hai đường thẳng rồi đúng không nào, bây giờ hãy vận dụng chúng để đi giải một số bài tập sau đây nha:

Bài 1:

Cho lăng trụ tam giác đều ABC, A’B’C’ có độ dài cạnh bằng a, AA’ = b, tính khoảng cách giữa AB và CC’.

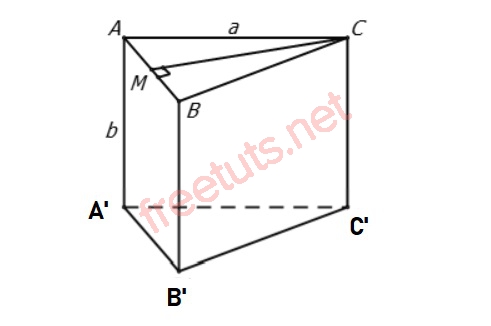
Ta có: CC’ // AA’, mà AA’ thuộc mặt phẳng (ABB’A’)

Nên suy ra CC’ // (ABB’A’)

Lúc này, ta có:

d(CC’; AB) = d(CC’; (ABB’A’)) = d(C; (ABB’A’).

Lấy M là trung điểm AB, chứng minh CM vuông góc với (ABB’A’)

Xét tam giác ABC đều nên ta có CM vừa là đường trung tuyến vừa là đường cao, ta có CM vuông góc với AB. (1)

Xét lăng trụ đều ABCA’B’C’ ta có, CM vuông góc với AA’ (2)

Ta có AB và AA’ thuộc ABB’A’. từ (1) và (2), suy ra

CM vuông góc với (ABB’A’).

d(C; (ABB’A’) = CM = CB.sin 60 = 1/2 (a căn 3).

Vậy khoảng cách giữa AB và CC’ bằng 1/2 (a căn 3).

Bài 2: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, tính khoảng cách giữa AA’ và BD’.

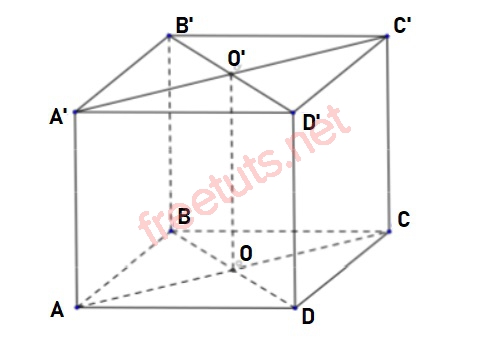
Lời giải:

Xét hình lập phương ABCD.A’B’C’D’, ta có:

AA’ // DD’, mà DD’ thuộc (BDD’B’) nên suy ra AA’ // (BDD’B’). Lúc này, ta có:

d(AA’; BD) = d(AA’, (BDD’B’) = d(A; BDD’B’).

Gọi O là giao điểm của BD và AC, O là trung điểm của BD.

Vì ABCD là hình vuông, nên ta có AO vuông góc với BD, và AO vuông góc với BB’ nên ta có:

AO vuông góc với (BDD’B’).

suy ra d(A, BDD’B’)) = AO.

Xét tam giác ABD, ta có:

1/(AO^2) = 1/(AB^2) + 1/(AD^2) = 1/(2^2) + 1/(2^2) = 1/2

Vậy AO = căn bậc 2 của 1/2, nên khoảng cách giữa AA’ và BD’ bằng căn bậc 2 của 1/2.

Như vậy, qua bài viết trên đây, freetuts.net đã tổng hợp toàn bộ kiến thức liên quan đến cách tính khoảng cách giữa 2 đường thẳng chéo nhau. Hy vọng rằng đây sẽ là những thông tin bổ ích giúp cho các bạn học sinh lớp 11 và 12 có thể tự tin giải các bài toán liên quan. Để biết thêm nhiều kiến thức thú vị về môn Toán, hãy truy cập website của chúng tôi thường xuyên nhé!