Hai tam giác động dạng là gì? Các trường hợp đồng dạng của tam giác

Bài này sẽ tổng hợp khái niệm hai tam giác đồng dạng là gì? Các tính chất và trường hợp hai tam giác được xem là đồng dạng.

Như các bạn đã biết, tam giác là là hình được tạo ra bởi ba điểm nằm trên các đường thẳng khác nhau nối lại với nhau. Có các loại tam giác thông thường như tam giác cân, tam giác đều, tam giác vuông và tam giác thường. Vậy hai tam giác đồng dạng là hai tam giác như thế nào? Hôm nay mình và các bạn cùng nhau tìm hiểu về khái niệm mới này nhé.

I. Khái niệm hai tam giác đồng dạng

1. Hai tam giác đồng dạng là gì?

Nhắc đến hai tam giác đồng dạng chúng ta có thể hiểu một cách khái quát rằng:

Hai tam giác được gọi là đồng dạng khi các góc của hai tam giác tương ứng bằng nhau và có các cạnh tương ứng tỉ lệ với nhau.

Bài viết này được đăng tại [free tuts .net]

Xét hai tam giác dưới đây.

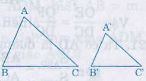
Tam giác A’B’C’ được gọi là tam giác đồng dạng với tam giác ABC nếu:

(! \hat{A'} = \hat{A} !), (! \hat{B'} = \hat{B} !) , (! \hat{C'} = \hat{C} !)

và

(!! \frac{A'B'}{AB} = \frac{B'C'}{BC} = \frac{A'C'}{AC} !!)

2. Tính chất của hai tam giác đồng dạng

• Tính chất giao hoán: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC thì tam giác ABC cũng đồng dạng với tam giác A’B’C’
• Tính chất bắc cầu: Nếu tam giác A’B’C’ đồng dạng với tam giác A’’B’’C’’, tam giác A’’B’’C’’ đồng dạng với tam giác ABC thì chúng ta có được cặp tam giác đồng dạng A’B’C’ và ABC

3. Định lí hai tam giác đồng dạng

Đối với hai tam giác đồng dạng chúng ta có định lí sau:

Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại của tam giác thì sẽ tạo thành một tam giác đồng dạng với tam giác đã cho.

II. Các trường hợp của hai tam giác đồng dạng

Sau đây là dấu hiệu nhận biết hai tam giác đồng dạng trong hình học.

Trường hợp 1: Cạnh- cạnh- cạnh

Trong trường hợp này hai tam giác đồng dạng với nhau khi ba cạnh của tam giác này bằng ba cạnh của tam giác kia. Đối với trường hợp này chúng ta sẽ không cần phải so sánh giá trị góc của hai tam giác với nhau.

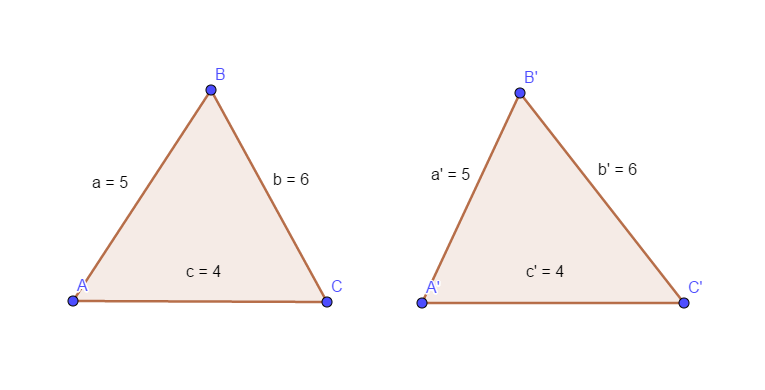
Ví dụ: Cho hai tam giác ABC và tam giác A’B’C’ đồng dạng với nhau thì

AB = A’B’ ; BC = B’C’ ; AC = A’C’

Trường hợp 2: góc - góc

Hai tam giác được gọi là hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh của chúng tương ứng bằng nhau.

Ví dụ: Cho tam giác ABC và tam giác A’B’C’, ta có:

• (! \hat{A} = \hat{A'} !)
• (! \hat{B} = \hat{B'} !)

=> △ A’B’C’ đồng dạng với △ ABC

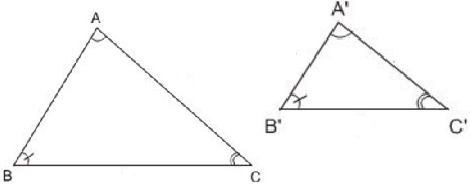
Trường hợp 3: góc - cạnh - góc

Trong trường hợp góc - cạnh- góc này thì hai tam giác được coi là hai tam giác đồng dạng với nhau khi hai góc và cạnh bên của cả hai tam giác đó bằng nhau.

Hoặc chúng ta có thể hiểu rằng, trường hợp này là hai tam giác đồng dạng khi hai cạnh có tỉ lệ bằng nhau và góc xen giữa hai cạnh của hai cạnh bằng nhau.

Ví dụ: Xét hai tam giác ABC và tam giác A’B’C’ đồng dạng với nhau khi:

(!! \frac{AB}{A'B'} = \frac{AC}{A'C'} !!) và (! \hat{A} = \hat {A'} !)

=> Tam giác A’B’C’ đồng dạng với tam giác ABC

III. Các định lí hai tam giác đồng dạng trong tam giác vuông

Định lí 1: Nếu cạnh huyền và cạnh góc góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau

Định lí 2: Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau

Định lí 3: Nếu góc nhọn của hai tam giác bằng nhau thì hai tam giác vuông đó là hai tam giác đồng dạng

IV. Bài tập chứng minh hai tam giác đồng dạng

Bài tập 1: Cho tam giác ABC có các cạnh tương ứng AB= 6cm, AC= 7cm và BC = 9cm. Tam giác A’B’C’ là một tam giác vuông tại A có A’B’= 12 cm, A’C’ = 14 cm. Hãy chứng minh hai tam giác trên đồng dạng với nhau.

Bài giải:

Ta có:

(! AB^2 + AC^2 = BC^2 !)

(!=> 6^2 + 7^2 = 9^2 = 81 !)

Vậy tam giác ABC là tam giác vuông tại A.

Xét tam giác ABC và tam giác A’B’C’ có:

(!! \hat{A} = \hat{A'} = 90 độ !!)

(!! \frac{AB}{AC} = \frac{A'B'}{A'C'} <=> \frac{6}{7} = \frac{12}{14} !!)

=> Tam giác A’B’C’ đồng dạng với tam giác ABC ( góc- cạnh- góc)

Trên đây là bài viết mình muốn giới thiệu cho các bạn về các dạng tam giác đồng dạng của hai hình tam giác. Các bạn hãy cố gắng nắm vững kiến thức để hỗ trợ cho việc học tập thật tốt nhé. Xin chào và hẹn gặp lại các bạn ở bài viết tiếp theo.