Bất đẳng thức Cosi: Công thức, hệ quả và các bài tập

Bất đẳng thức Cosi hay còn gọi là bất đẳng thức AM - GM là BĐT được dùng để so sánh giữa trung bình cộng và trung bình nhân của các số thực không âm.

Bất đẳng thức Cosi là một kiến thức toán học vô cùng quan trọng trong chương trình THCS, đây là tiền đề giúp các em học sinh lớp 8 và 9 giải các bài toán liên quan đến phương trình và bất phương trình hiệu quả nhất. Chính vì vậy, trong bài viết hôm nay, hãy cùng freetuts ôn tập lại các kiến thức liên quan đến bất đẳng thức Cauchy và các dạng bài tập liên quan nha.

Tìm hiểu về bất đẳng thức Cosi

Định nghĩa bất đẳng thức Cosi

Trong toán học, bất đẳng thức Cô si là bất đẳng thức được dùng để so sánh giữa trung bình cộng và trung bình nhân của các số thực không âm.

Ai là người phát minh ra bất đẳng thức Cosi?

Tên đúng của bất đẳng thức này là hay có tên khác là bất đẳng thức AM - GM, trong đó: AM là viết tắt của Arithmetic mean, GM là viết tắt của Geometric mean. Và BĐT này có rất nhiều cách chứng minh nhưng nhà toán học người Pháp là Augustin – Louis Cauchy (Cosi, theo cách đọc tiếng Việt) đã đưa ra cách chứng minh quy nạp dễ hiểu nhất nên nhiều người đã nhầm lẫn rằng BĐT AM - GM là do ông phát minh ra.

Bài viết này được đăng tại [free tuts .net]

Bất đẳng thức Cô si được dùng để làm gì?

Bất đẳng thức Cauchy là một trong những kiến thức vô cùng quan trọng và phổ biến trong chương trình toán THCS, nó được sử dụng để giải các dạng toán liên quan đến phương trình, bất phương trình và tìm giá trị lớn nhất hay bé nhất của biểu thức.

Các dạng bất đẳng thức Cosi trong toán học

Bất đẳng thức AM - GM (Cosi) có thể được phát biểu dưới các dạng sau:

Dạng 1: Dạng tổng quát bđt Cosi

Trung bình cộng của n số thực không âm sẽ luôn luôn lớn hơn hoặc bằng trung bình nhân của các số thực này, và trung bình cộng chỉ bằng trung bình nhân khi n số thực này bằng nhau.

• Với 2 số thực a, b không âm, ta có:

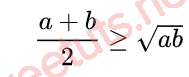
Dấu “=” xảy ra khi a = b.

• Với 3 số thực a, b và c không âm, ta có:

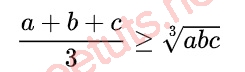
Dấu “=” xảy ra khi a = b = c.

• Bất đẳng thức Cosi mở rộng với x1, x2,...xn, n là số thực không âm, ta có:

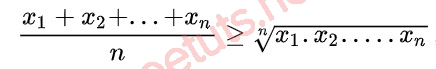
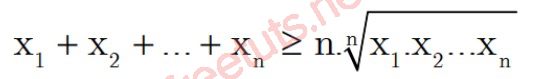
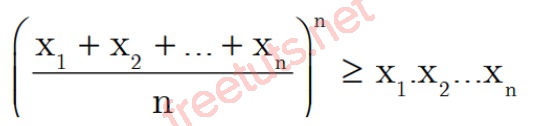
Dấu “=” xảy ra khi x1 = x2 =...xn.

Với x1, x2,...xn, n là số thực dương, ta có:

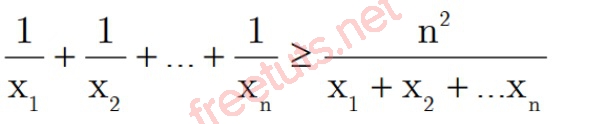
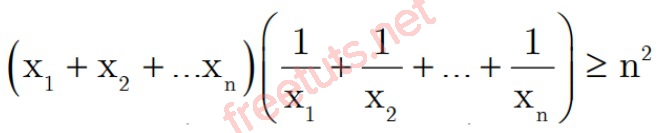
Dấu “=” xảy ra khi x1 = x2 =...xn.

Dạng 2: Các trường hợp đặc biệt của bất đẳng thức Cauchy

Trong trường hợp n = 2 và n = 3, ta có một số dạng biểu diễn đặc biệt như sau:

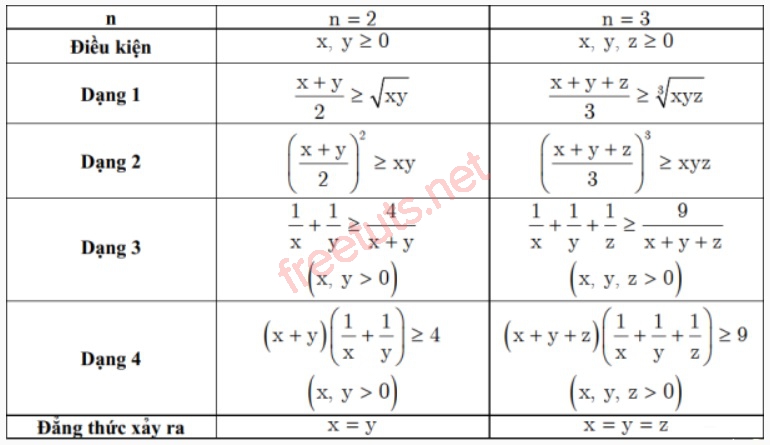
Dạng 3: Một số bất đẳng thức được suy ra từ bđt Cauchy

Từ bất đẳng thức Cô si, chúng ta có thể suy ra một số bất đẳng thức khác như sau:

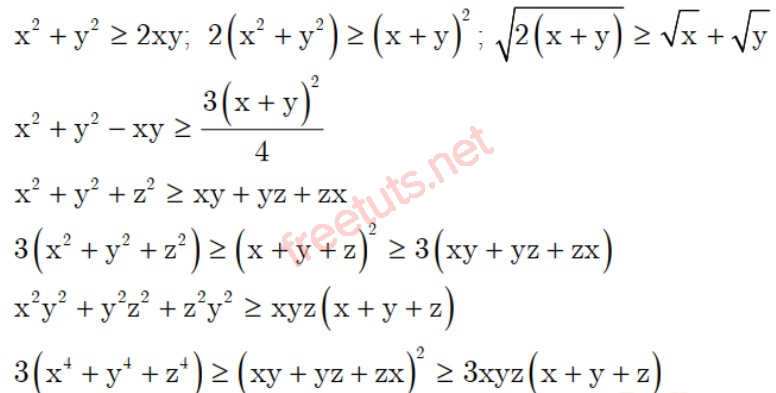
Hệ quả bất đẳng thức Cosi lớp 9

Từ bất đẳng thức Cauchy, chúng ta có một số hệ quả sau:

• Hệ quả 1: Cho một số thực dương, ta luôn có tổng của nó và số nghịch đảo của chính nó luôn đạt giá trị nhỏ nhất là 2.

a + 1/a ≥ 2, ∀ a > 0

• Hệ quả 2: Cho hai số thực dương bất kỳ (a, b), nếu tổng (a+b) không đổi thì tích của (a.b) có giá trị lớn nhất khi a = b.
• Hệ quả 3: Cho hai số thực dương bất kỳ, nếu tích của nó không đổi thì tổng của 2 số này có giá trị nhỏ nhất khi 2 số này bằng nhau.

Cách chứng minh bất đẳng thức Cauchy

Có rất nhiều cách chứng minh bất đẳng thức Cauchy, các em hãy cùng tham khảo một số các phương pháp chứng minh bất đẳng thức này ngay bên dưới đây nha:

Chứng minh bất đẳng thức Cosi cho 2 số dương

Cho a, b ∈ R; chứng minh rằng:

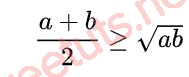
⇔ a + b ≥ 2 căn bậc 2 của (a x b)

⇔ a - 2 căn bậc 2 của (a x b) + b ≥ 0

⇔ (căn a - căn b)^2 ≥ 0 (luôn đúng với mọi a, b ≥ 0)

Như vậy, ta đã chứng minh được BĐT cauchy luôn đúng với 2 số thực dương.

Chứng minh bất đẳng thức cosi cho 3 số thực không âm

Với a, b, c là số thực dương, hãy chứng minh BĐT sau:

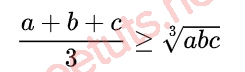
Ta có:

Đặt x = căn bậc 3 của a, y = căn bậc 3 của b, z = căn bậc 3 của c, nên ta có x, y, z ≥ 0,

⇒ x + y + z ≥ 0.

Lúc này, bất đẳng thức quy về dạng

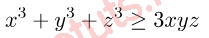
Vậy ta có điều cần chứng minh, và dấu “=” xảy ra khi và chỉ khi x = y = z, hay tương đương a = b = c.

Chứng minh BĐT Cosi với n số thực không âm

Với x1, x2,...xn, n là số thực không âm, hãy chứng minh BĐT sau là đúng.

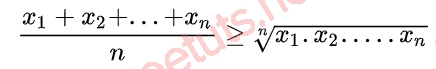
Ta đã chứng minh được BĐT Cosi luôn đúng với 2 số thực dương, suy ra n = 2 thì BDT Cosi trên luôn đúng.

Để chứng minh BĐT trên đúng với n số thì chúng ta có thể chứng minh nó cũng đúng với 2n số.

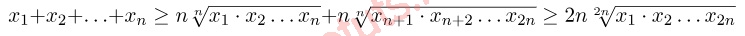
Áp dụng tính chất quy nạp, ta có bất đẳng thức trên sẽ luôn đúng với n là một lũy thừa của 2.

Gỉa sử BĐT Cosi luôn đúng với n số, ta cũng sẽ chứng minh được nó luôn đúng với n - 1 số như sau:

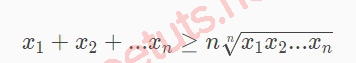
Gọi xn = S/(n - 1), với S = x1 + x2 +...+ xn

Suy ra:

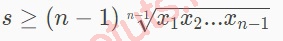
Như vậy, ta có, BĐT Cosi luôn đúng với 2n và (n - 1) số, vậy, ta có thể suy ra bất đẳng thức Cauchy sẽ đúng với n số thực không âm.

Lưu ý khi sử dụng bất đẳng thức AM - GM (Cosi)

Khi sử dụng bất đẳng thức Cauchy, các bạn cần lưu ý một số điều sau:

• Bất đẳng thức Co si chỉ đúng với các số thực không âm.
• Chỉ nên áp dụng bất đẳng thức Cô si khi BĐT cần chứng minh có tổng và tích.
• Luôn nhớ, dấu “=” chỉ xảy ra khi các số bằng nhau.

Dạng bài tập về bất đẳng thức Cosi

Như vậy, các em đã nắm được các kiến thức liên quan đến BĐT Cosi rồi đúng không nào, bây giờ hãy áp dụng chúng để đi giải một số dạng bài tập mà freetuts đã liệt kê ngay bên dưới đây nha:

Dạng 1: Áp dụng trực tiếp BĐT Côsi trong bài tập chứng minh bất đẳng thức

Ví dụ: Cho 2 số dương a, b thỏa mãn a^2 + b^2 = 2, hãy chứng minh:

(a/b + b/a)(a/b^2 + b/a^2) ≥ 4

Lời giải:

Vì a, b > 0 nên suy ra a/b > 0, b/a > 0, a/b^2 > 0, b/a^2 >0.

Áp dụng bdt Cosi, ta có:

a/b + b/a ≥2 căn bậc hai (a/b x b/a) = 2

a/b^2 + b/a^2 ≥2 căn bậc hai (a/b^2 + b/a^2 ) = 2/(căn bậc 2(a x b)

Suy ra:

(a/b + b/a)(a/b^2 + b/a^2) ≥ 4/(căn bậc 2 của a x b) (1)

Mà ta có:

2 = a^2 + b^2 ≥ 2 x (căn bậc 2 của a^2 x b^2) = 2.a.b

⇒ a.b ≤ 1 (2)

Kết hợp (1) và (2), ta có:

(a/b + b/a)(a/b^2 + b/a^2) ≥ 4 (điều phải chứng minh),

Dấu “=” xảy ra khi a = b = 1.

Dạng 2: Kỹ thuật thêm bớt trong bất đẳng thức Côsi

Đối với dạng toán này, các em hãy biến đổi BĐT cần phải chứng mình bằng cách nhân, chia hoặc thêm bớt một số, để có thể đơn giản được BĐT ban đầu.

Lưu ý: Khi tách và áp dụng BDT cosi, phải dựa vào việc đảm bảo cho dấu “=” xảy ra.

Ví dụ: Cho a, b là số thực dương, sao cho a > b, chứng minh rằng:

a + 1/(b.(a - b) ≥ 3.

Lời giải:

Coi 1/(b.(a - b), b, (a - b) là 3 số dương, ap dụng bất đẳng thức Co si cho 3 số dương ta có:

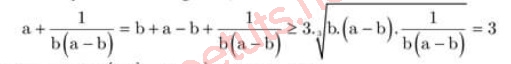
Dấu bằng xảy ra, khi và chỉ khi:

a - b = b = 1/(b.(a - b) ⇔ a = 2; b = 1.

Dạng 3: Tìm giá trị lớn nhất, bé nhất của biểu thức

Ví dụ: Bài tập tìm GTLN, GTNN bằng bất đẳng thức Cosi lớp 9

Cho hai số dương a, b. Tìm giá trị lớn nhất (GTLN) hoặc giá trị nhỏ nhất (GTNN) của các biểu thức trong trường hợp sau:

a. a + b = 8, tìm GTLN của A = (a + b ).a.b

b. a.b = 6 không đổi, tìm GTNN của biểu thức B = (a + b)/ (a^2.b^2)

Lời giải:

Vì a + b = 8 nên ta có A = (a + b ).a.b = 8ab.

Áp dụng hệ quả bất đẳng thức cô si, ta có:

A đạt GTLN khi và chỉ khi (a x b) max ⇔ a = b (1)

Ta có: a + b = 8, a = b ⇒ a = b = 4.

Vậy A max = 6.4.4 = 96.

Vậy A đạt giá trị lớn nhất là 96 khi a = b = 4.

b. Ta có B = (a + b)/ (a^2.b^2) = (a + b)/9^2 = (a + b)/81 vì a.b = 9 luôn không đổi.

Áp dụng hệ quả BĐT cosi, ta có:

B min ⇔ (a + b) min ⇔ a = b.

Lúc này ta có: a = b; a.b = 9 ⇒ a = b = 3.

Vậy B min = (3 + 3)/81 = 2/27

Vậy giá trị nhỏ nhất của B là 2/27 khi a = 3 = 3.

Dạng 4: Ứng dụng BDT Cosi ngược dấu để chứng minh bất đẳng thức

Ví dụ minh họa bài tập về bất đẳng thức Cosi lớp 9

Cho 3 số thực a, b , c không âm, lớn hơn 0 và a + b + c = 3, chứng minh rằng:

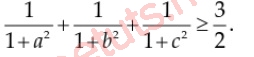
Lời giải:

Vì a + b + c = 3; a, b, c >0, nên ta thấy điểm rơi của bpt tại a = b = c = 1.

Áp dụng bđt Cosi cho mẫu số, ta có:

a^2 + 1 ≥ 2a ⇔ 1/(1+a^2) ≤ 1/2a

Ta thấy, lúc này dấu của bdt sẽ ngược chiều so với yêu cầu của đề bài.

Lúc này, áp dụng Cosi ngược dấu, ta có:

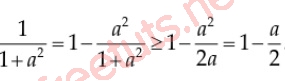
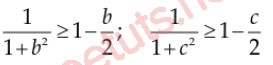
Cộng vế theo vế, ta có:

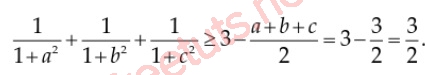
Vậy ta đã có điều phải chứng minh.

Hỏi đáp về BDT Cosi

Bất đẳng thức Cosi học ở lớp mấy?

Các em sẽ được học kiến thức về BĐT Cosi trong chương trình toán lớp 9 nha.

Bất đẳng thức Cauchy-Schwarz có phải là tên gọi khác của BĐT Cosi không?

Các em đừng nhầm lẫn giữa điều này nha, hai BĐT này hoàn toàn khác nhau đó, BĐT Cauchy-Schwarz hay còn gọi là bất đẳng thức Bunhiacopxki là BĐT do 3 nhà toán học Augustin Louis Cauchy, Viktor Yakovlevich Bunyakovsky và Hermann Amandus Schwarz phát minh ra.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ các kiến thức liên quan về bất đẳng thức Cosi, các công thức, cách chứng minh và một số dạng bài tập liên quan. Hy vọng bài viết nãy sẽ giúp các em ôn luyện và nắm vững được kiến thức quan trọng này. Chào tạm biệt và hẹn gặp lại các em trong các bài đăng tiếp theo để cùng nhau tìm hiểu thêm nhiều kiến thức toán học thú vị khác nha!