Tiệm cận đứng của đồ thị hàm số, cách tìm và các dạng bài tập

Tiệm cận đứng là một khái niệm quan trọng trong chương trình toán 12, đồ thị hàm số có tiệm cân đứng khi giới hạn của hàm số đó tiến tới giá trị cố định vô cùng.

Tiệm cận đứng là một dạng bài toán thường xuyên xuất hiện trong các đề thi THPT Quốc gia, tuy nó không hề khó nhưng cũng có nhiều em học sinh khá bối rối trong việc hệ thống lại các kiến thức liên quan đến dạng toán này. Trong bài viết hôm nay, freetuts sẽ giúp các em củng cố lại những kiến thức quan trọng liên quan đến tiệm cận đứng và một số dạng bài tập liên quan nha.

Ý nghĩa của tiệm cận đứng đối với đồ thị hàm số

Định nghĩa đường tiệm cận đứng

Tiệm cận đứng (TCĐ) của đồ thị hàm số y = f(x) là đường thẳng x = x₀ nếu thỏa mãn một trong hai điều kiện sau:

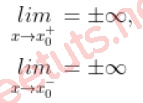
Bài viết này được đăng tại [free tuts .net]

Tại sao phải tìm tiệm cận đứng của một hàm số?

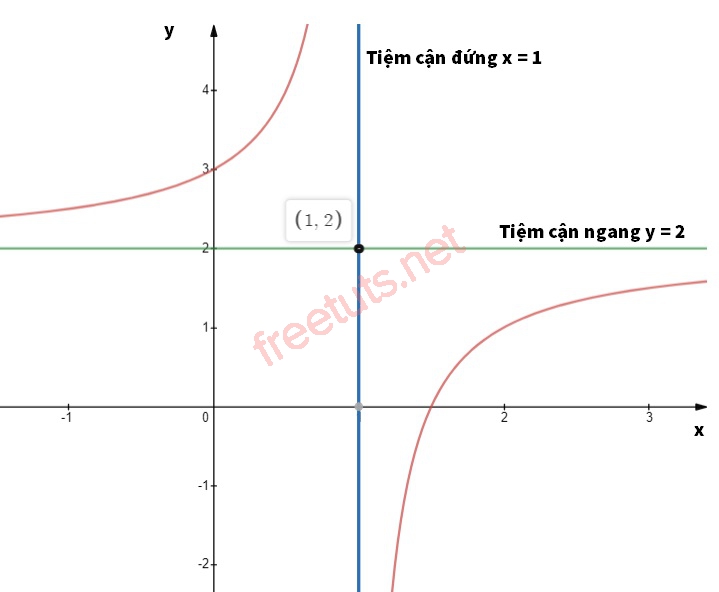
Đường tiệm cận đứng của hàm số y = f(x).

Cũng như đường tiệm cận ngang, TCĐ cũng là một khái niệm vô cùng quan trọng trong chương trình toán THPT vì những lý do sau:

• Khi bạn xác định được TCĐ của một hàm số, nó sẽ cung cấp thông tin quan trọng về hướng tiến gần đến vô hạn của đồ thị hàm số đó khi x tiến tới 1 giá trị xác định.
• Việc xác định TCĐ là vô cùng quan trọng và cần thiết để giúp bạn xác định giới hạn, điểm cực đại, cực tiểu của hàm số đó.

Cách tìm tiệm cận đứng của một hàm số bất kỳ

Sử dụng máy tính bỏ túi Casio để tìm đường TC.

Hướng dẫn cơ bản

Để tìm được TCĐ của đồ thị hàm số bất kỳ, các em hãy thực hiện theo các bước sau nha:

Bước 1: Đầu tiên, hãy xác định tập xác định D của hàm số đã cho.

Bước 2: Hãy tìm điểm không xác định của hàm số đó, nhưng có lân cận trái hoặc lân cận phải nằm trong tập xác định.

Bước 3: Tính giới hạn một bên của hàm số tại các điểm đã tìm được ở bước 2 và rút ra kết luận.

Ví dụ minh họa:

Tìm đường TCĐ của đồ thị y = (2x -3)/(x-1).

Lời giải:

Xét hàm số y = (2x -3)/(x-1) không xác định khi x - 1 = 0, tương đương x = 1.

Với x = 1, ta có:

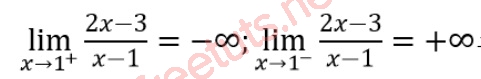
Vậy x = 1 là TCĐ của đồ thị y = (2x -3)/(x-1).

Tìm tiệm cận đứng bằng máy tính bỏ túi Casio

Đường thẳng x = x0 được coi là đường TCĐ của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau:

• lim x →x0+f(x)=+∞(–∞)
• limx→x0–f(x)=+∞(–∞)

Phương pháp giải trên máy tính như sau:

Bước 1: Tìm các giá trị x0 để hàm số y = f(x) không xác định, thường cho mẫu số = 0 và giải phương trình tìm x0.

Bước 2:

• Tính limx→x0+f(x), nhập f(x), chọn CALC, chọn x = x0 +0,00001
• Tính limx→x0-f(x), nhập f(x), chọn CALC, chọn x = x0 - 0,00001

Lúc này, kết quả có thể rơi vào 4 trường hợp như sau:

• TH1: Một số dương rất lớn, lúc này ta sẽ kết luận giới hạn bằng dương vô cùng.
• TH2: Một số âm rất nhỏ, lúc này ta sẽ kết luận giới hạn bằng âm vô cùng.
• TH3: Một số bất kỳ có dạng A.10-n, lúc này ta sẽ kết luận giới hạn bằng 0.
• TH4: Một số tự nhiên bình thường là B, lúc này ta sẽ suy ra giới hạn bằng B.

Ví dụ minh họa:

Tìm đường TCĐ của đồ thị hàm số sau:

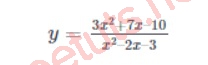
Lời giải:

Xét đồ thị hàm số y không xác định khi mẫu = 0, ta có:

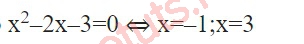
Với x = -1, x = 3, hãy lần lượt nhập theo bước sau:

• Tính limx→x0+f(x), nhập f(x), chọn CALC, chọn x = -1 +0,00001 = dương vô cùng.
• Tính limx→x0-f(x), nhập f(x), chọn CALC, chọn x = -1 - 0,00001 = âm vô cùng.
• Tính limx→x0+f(x), nhập f(x), chọn CALC, chọn x = 3 +0,00001 = dương vô cùng.
• Tính limx→x0-f(x), nhập f(x), chọn CALC, chọn x = 3 - 0,00001 = âm vô cùng.

Vậy ta kết luận, đồ thị có 2 đường TCĐ lần lượt là x = -1 và x = 3.

Tìm tiệm cận đứng qua bảng biến thiên

Ngoài 2 cách trên, các em có thể tìm được đường TCĐ của hàm số dựa vào bảng biến thiên, chi tiết cách làm như sau:

Bước 1: Tìm tập xác định D của hàm số đã cho dựa vào bảng biến thiên.

Bước 2: Quan sát kỹ bảng biến thiên và xác định những điểm khiến hàm số không xác định, những điểm đó là TCĐ của hàm số đó.

Ví dụ minh họa:

Cho hàm số xác định và liên tục có bảng biến thiên như sau:

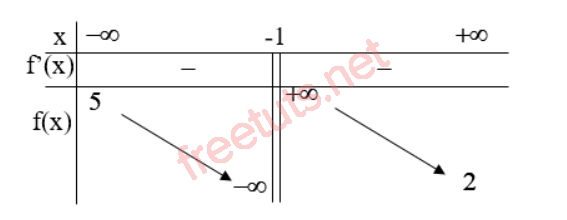
Hãy tìm đường TCĐ của hàm số này.

Lời giải:

Xét bảng biến thiên, ta có:

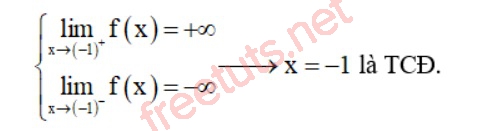
Vậy x = -1 là đường TCĐ cần tìm.

Công thức đường tiệm cận đứng trong toán học

Sau đây là công thức tính nhanh TCĐ của hàm số phân tuyến tính bất kỳ, các em hãy ghi nhớ để áp dụng giải toán thật nhanh nha:

Tiệm cận đứng của hàm số phân tuyến tính: y = (ax + b)/(cx + d), với (ad - bc khác 0, c khác 0) là x = (-d)/c.

Ví dụ: Cho hàm số y = f(x) = (x - 4)/(x + 5). Tìm TCĐ của hàm số này theo phương pháp tính nhanh.

Cách giải:

Dựa vào hàm số đã cho, ta có (1 x 5 ) - (4 x 1) = 1, khác 0, và 5 khác 0, như vậy TCĐ của hàm số là x = -5/1 = -5.

Dạng bài tập liên quan đến tiệm cận đứng và cách giải

Mời các em cùng tham khảo một số dạng bài tập liên quan đến đường TCĐ và cách giải chi tiết mà freetuts đã tổng hợp được ở dưới đây nha.

Dạng 1: Tìm đường tiệm cận đứng dựa vào định nghĩa

Đối với dạng này, các em cần phải nắm vững định nghĩa về đường TCĐ và áp dụng nó để giải một cách dễ dàng ha.

Ví dụ: Cho đồ thị hàm số sau, hãy tìm tiệm cận đứng của hàm số y = (2x -3)/(x - 1), D = R\ {1}.

Hướng dẫn giải:

Ta có:

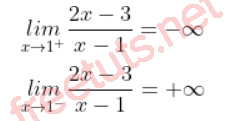
Vậy, x = 1 là đường TCĐ cần tìm.

Dạng 2: Tìm tiệm cận đứng của đồ thị hàm số phân tuyến tính

Đối với dạng bài này, các em chỉ cần nhớ công thức tính nhanh đường TCĐ của hàm số phân tuyến tính là có thể dễ dàng tìm được đáp án rồi nè.

Ví dụ: Cho đồ thị hàm số y = f(x) = (1 - 3x)/(x + 2), hãy tìm đồ thị của hàm số này.

Hướng dẫn giải:

Áp dụng công thức tính nhanh đồ thị hàm số phân tuyến tính, ta có, x = (-2)/1 = -2 là TCĐ của hàm số đã cho.

Dạng 3: Tìm tham số m để hàm số bất kỳ có tiệm cận đứng

Để giải được dạng toán này, các em hãy xem lại hướng dẫn tìm hàm số cơ bản đã nêu ở trên để áp dụng nha.

Ví dụ: Cho hàm số y = (3x +1)/(m - 2x), m phải bằng bao nhiêu để hàm số đã cho có đường tiệm cận đứng là x = 1.

Hướng dẫn giải:

Dựa vào đồ thị, ta có x = (-1)/3 là nghiệm của tử số, vậy để đồ thị hàm số đã cho có tiệm cận thì x = (-1)/3 không phải là nghiệm của phương trình m - 2x = 0 ⇒ m khác (-2)/3.

Để đồ thị hàm số đã cho nhận x = 1 là TCĐ thì m/2 = 1 ⇒ m =2.

Vậy m = 2 thì hàm số y = (3x +1)/(m - 2x) có TCĐ là x = 1.

Bài tập về tiệm cận đứng của đồ thị hàm số

Sau đây là một số bài tập liên quan đến lý thuyết tiệm cận đứng, các em hãy cùng giải để vừa thử sức mình và ôn luyện lại kiến thức nha:

Bài 1: Tìm TCĐ của đồ thị hàm số y = ( 3 - x)/(x - 2).

Lời giải:

Ta có: lim(x→2)(2-x)/x-2) = -∞, vậy suy ra x = 2 là đường TCĐ của đồ thị y = ( 3 - x)/(x - 2).

Bài 2: Đồ thị hàm số sau có bao nhiêu đường TCĐ?

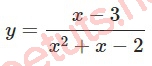
Ta có đường thằng x = x0 là TCĐ của đồ thị hàm số y = f(x)/g(x) nếu x0 là nghiệm của g(x) nhưng không phải là nghiệm của f(x).

Xét hàm số x^2 + x - 2 = 0, ta có x = 1 và x = 2.

Với x = 1 và x = 2 thì x - 3 khác 0,

Vậy đồ thị hàm số y đã cho có 2 TCĐ là x = 1 và x = 2.

Hy vọng với những chia sẻ trên đây của freetuts.net, các em có thể dễ dàng hệ thống lại các kiến thức liên quan đến đường tiệm cận đứng, từ đó có thể tự tin giải các bài tập liên quan. Chúc các em có kết quả học tập thật tốt nha. Đừng quên ghé thăm chuyên mục môn học của chúng tôi để có thể ôn tập lại nhiều kiến thức quan trọng khác nha.