Tổng hợp các tác giả văn học hiện đại Việt Nam 
Số tự nhiên là gì? Sự khác nhau giữa tập hợp N và N* 
Tiểu sử nhà văn Tô Hoài: Sự nghiệp sáng tác văn học của ông 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Đường trung tuyến, định nghĩa, tính chất và các dạng bài tập
Đường trung tuyến trong tam giác là đoạn thẳng nối từ 3 đỉnh của tam giác đến trung điểm của 3 cạnh đối diện, mỗi tam giác sẽ có duy nhất 3 đường trung tuyến.
Đường trung tuyến là một bài học quan trọng trong bộ môn Hình học lớp 10, tuy nhiên chắc hẳn nhiều em học sinh còn đang bối rối trong việc ghi nhớ các kiến thức liên quan tới đường đặc biệt này. Trong bài viết hôm nay, hãy cùng freetuts đi sâu tìm hiểu các kiến thức liên quan tới đường trung tuyến nha.
Định nghĩa đường trung tuyến trong toán học
Đường trung tuyến của một đoạn thẳng bất kỳ là đường thẳng đi qua trung điểm của đoạn thẳng đó.
Đường trung tuyến của một tam giác là đoạn thẳng xuất phát từ các đỉnh của tam giác tới trung điểm của cạnh đối diện, mỗi tam giác sẽ có 3 đường trung tuyến ứng với 3 đỉnh.
Bài viết này được đăng tại [free tuts .net]
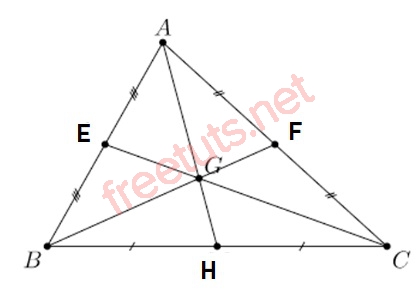
Hình ảnh minh họa về 3 đường trung tuyến trong tam giác.
Ví dụ minh họa:
Cho tam giác ABC, trong đó E, F, H lần lượt là 3 trung điểm ứng với 3 cạnh AB, AC và BC, lúc này ta có AH, BF và CE lần lượt là 3 đường trung tuyến của tam giác ABC.
Tính chất đường trung tuyến
Cùng tìm hiểu các tính chất đặc biệt của đường trung tuyến trong tam giác thường, tam giác vuông, cân, đều ngay bên dưới đây nha.
Tính chất đường trung tuyến trong tam giác bất kỳ
Cho một tam giác bất kỳ, đường trung tuyến của tam giác này sẽ có những tính chất sau:
- Tính chất 1: 3 đường trung tuyến của tam giác này sẽ cùng cắt nhau (đồng quy) tại một điểm. điểm này chính là trọng tâm của tam giác.
- Tính chất 2: Khoảng cách từ trọng tâm của tam giác này đến các đỉnh đúng bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Ví dụ minh họa:
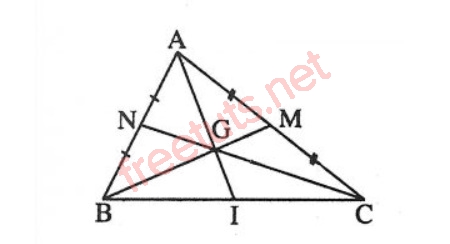
Tam giác ABC có G là giao điểm 3 đường AI, BM và CN.
Cho tam giác ABC, lần lượt có 3 đường trung tuyến là AI, BN và CN cắt nhau tại G, biết AI = 6, tính độ dài đoạn AG = ?
Lời giải:
Vì G là giao điểm của 3 đường trung tuyến ABC, nên G là trọng tâm của tam giác ABC.
Áp dụng tính chất của 3 đường trung tuyến, ta có:
AG = 2/3 AI = 2/3 . 6 = 4.
Tính chất đường trung tuyến trong tam giác vuông
Cho tam giác vuông, đường trung tuyến của tam giác vuông sẽ có một số tính chất đặc biệt sau:
- Tính chất 1: Đường trung tuyến ứng với cạnh huyền có số đo bằng ½ cạnh huyền.
- Tính chất 2: Nếu một tam giác có đường trung tuyến bằng 1/2 cạnh huyền thì tam giác đó sẽ là tam giác vuông.
Ví dụ minh họa: Cho tam giác ABC vuông tại A, cạnh AB = 10, AC = 8, BC = 12, AM là đường trung tuyến ứng với cạnh BC, tính độ dài AM.
Lời giải:
Áp dụng tính chất 1, ta có:
Công thức đường trung tuyến trong tam giác vuông ABC là:
AM = 1/2 BC = 1/2. 12 = 6.
Tính chất đường trung tuyến trong tam giác cân, tam giác đều
- Tính chất 1: Trong tam giác cân hoặc tam giác đều, đường trung tuyến của cạnh đáy sẽ luôn vuông góc với cạnh đáy và đường này sẽ chia tam giác thành hai tam giác có kích thước bằng nhau.
- Tính chất 2: Trong tam giác đều, ba đường trung tuyến sẽ có độ dài bằng nhau.
Định lý đường trung tuyến
Có 3 định lý ứng với 3 tính chất của đường trung tuyến là:
- Định lý 1: Trong một tam giác, ba đường trung tuyến sẽ cùng đi qua một điểm, điểm này chính là trọng tâm của tam giác.
- Định lý 2: Đường trung tuyến của một tam giác bất kỳ sẽ chia tam giác ấy thành hai tam giác nhỏ hơn có diện tích bằng nhau. Vậy 3 đường trung tuyến sẽ chia tam giác lớn thành 6 tam giác nhỏ có diện tích bằng nhau.
- Định lý 3: Trọng tâm của tam giác cách mỗi đỉnh đúng bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh ấy.
Công thức đường trung tuyến trong tam giác lớp 10
Cho tam giác ABC, trong đó a, b, c lần lượt là độ dài các cạnh của tam giác, ma, mb, mc là 3 đường trung tuyến ứng với 3 đỉnh A, B và C. Ta có độ dài đường trung tuyến sẽ được tính theo công thức sau:
Ví dụ minh họa:
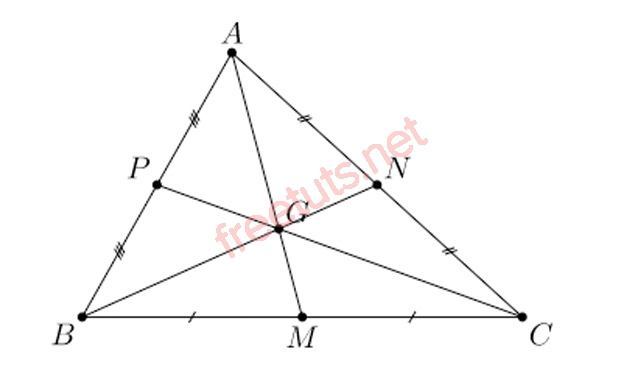
Hình ảnh 3 đường trung tuyến trong tam giác ABC.
Cho tam giác ABC, độ dài cạnh AB = 3, AC = 5, BC = 6, tính độ dài đường trung tuyến AM, BN và CP.
Lời giải:
Áp dụng công thức tính độ dài đường trung tuyến, ta có:
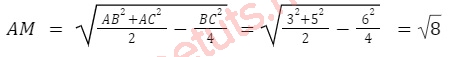
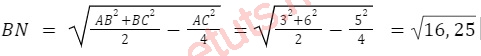
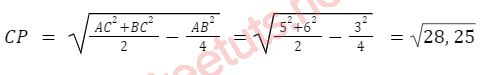
Dạng bài tập liên quan đến đường trung tuyến
Hãy cùng vận dụng những kiến thức ở trên để cùng đi giải một số dạng bài tập mà freetuts đã tổng hợp ngay bên dưới đây để vừa ôn luyện lý thuyết vừa thử sức mình nha.
Dạng 1: Chứng minh đường thẳng là đường trung tuyến
Ví dụ:
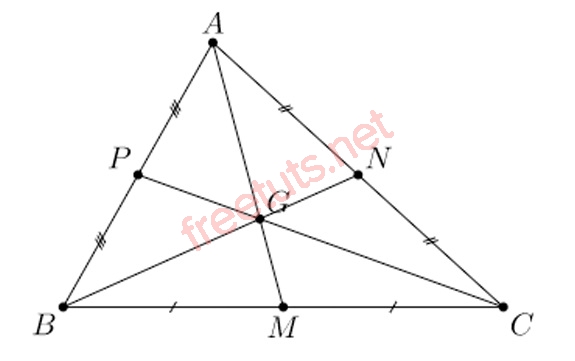
Tam giác ABC.
Cho tam giác ABC, trong đó P, N lần lượt là trung điểm của cạnh AB và AC, biết CP và BN cắt nhau tại G, chứng minh AG là đường trung tuyến ứng với cạnh BC của tam giác ABC.
Lời giải:
Vì P, N là trung điểm của cạnh AB và AC nên ta có BN và CP sẽ lần lượt là 2 đường trung tuyến của tam giác ABC, mà BN và Cp cắt nhau tại G, nên suy ra AG sẽ là đường trung tuyến còn lại của tam giác ABC.
Dạng 2: Áp dụng các tính chất của đường trung tuyến
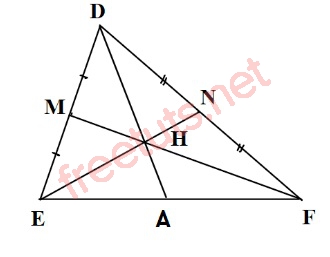
Tam giác DEF.
Cho tam giác DEF có hai đường trung tuyến cắt nhau tại H, DH kéo dài cắt EF tại A, chứng minh rằng AE = AF.
Lời giải:
Theo đề bài, ta có H là giao điểm của hai đường trung tuyến EN và FM, nên suy ra H là trọng tâm của tam giác ABC.
Nên DH sẽ là đường trung tuyến thứ ba ứng với cạnh EF, DH lại cắt EF tại A, nên lúc này A sẽ trở thành trung điểm của cạnh EF.
Vậy ta sẽ có AE = AF.
Dạng 3: Đường trung tuyến trong tam giác vuông, cân, đều
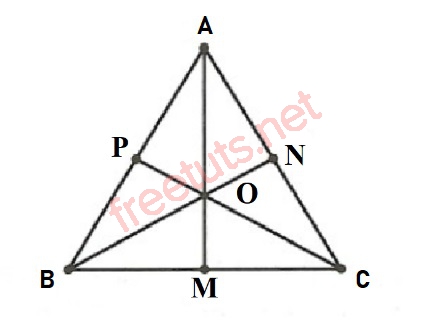
Tam giác đều ABC.
Ví dụ: Cho tam giác đều ABC có 3 đường trung tuyến lần lượt là AM, BN và CP cắt nhau tại O. Hãy chứng minh OB = OM = OC.
Lời giải:
Vì tam giác ABC có 3 đường trung tuyến cắt nhau tại điểm O, nên O là trọng tâm của tam giác ABC, suy ra ta có công thức đường trung tuyến trong tam giác đều ABC là:
OA = 2/3 AM, OB = 2/3 BN, OC = 2/3 CP.
Áp dụng tính chất 3 đường trung tuyến trong tam giác đều, ta có AM = BN = CP
Vậy suy ra:
OA = OB = OC.
Dạng 4: Bài tập nâng cao
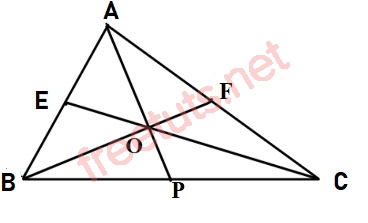
Tam giác ABC.
Ví dụ: Cho tam giác ABC, có 3 đường trung tuyến là AP, BF và CE cắt nhau tại O. Hãy chứng minh rằng diện tích tam giác OCP = diện tích tam giác COF.
Lời giải:
Xét tam giác ABC, ta có 3 đường trung tuyến cắt nhau tại điểm O, nên O sẽ là trọng tâm của tam giác ABC, suy ra:
OP = AP - OA = AP - 2/3 AP = 1/3 AP.
OF = BF - OB = BF - 2/3 BF = 1/3 BF.
Xét 2 tam giác OCP và ACP có cùng chiều cao hạ từ đỉnh C (gọi chiều cao này là h), lúc này ta có.
S(ACP) = 1/2 AP. h, S(COP) = 1/2OP.h
mà ta có OP = 1/3AP, nên suy ra S(OCP) = 1/3.S(ACP).
Áp dụng định lý 2, ta có S(ACP) = 1/2 S(ABC), vậy S(OCP) = 1/6 S(ABC).
Tương tự ta cũng chứng minh được S(COF) = 1/6 S(ABC).
Vậy ta đã chứng minh được diện tích tam giác OCP = diện tích tam giác COF.
Hỏi đáp liên quan đến đường trung tuyến
Giao 3 đường trung tuyến là gì?
Trong một tam giác, giao điểm của 3 đường trung tuyến là trọng tâm của tam giác.
Trong tam giác đều đường trung tuyến đồng thời là đường gì?
Trong tam giác đều, đường trung tuyến đồng thời là đường trung trực, đường phân giác mà còn là đường cao của tam giác đó.
Trong tam giác cân, đường trung tuyến đồng thời là đường gì?
Trong tam giác cân, đường trung tuyến cũng là đường cao của tam giác.
Như vậy, qua bài viết trên, freetuts.net đã chia sẻ các kiến thức về định nghĩa, tính chất cũng như công thức và một số dạng bài tập liên quan đến đường trung tuyến. Hy vọng đây sẽ là những thông tin hữu ích dành cho các bạn học sinh lớp 10. Chúc các em vận dụng tốt những kiến thức này để có thể đạt kết quả cao trong môn Toán nha.
