Các dạng bài toán tìm đường kính hình tròn thường gặp

Trong chủ đề hình tròn, cách tính đường kính của hình tròn đó là một vấn đề thiết yếu mà các bạn cần phải năm rõ, nó giúp ta giải các bài tập về tính diện tích và chu vi.

Bài học ngày hôm nay mình sẽ tổng hợp cho các bạn các cách tính đường kính hình tròn một cách dễ hiểu nhất để giúp các bạn có thể áp dụng nó vào bài giải một cách đơn giản.

1. Đường kính hình tròn là gì?

Các bạn đã nghe rất nhiều về đường kính, vậy đường kính hình tròn là gì?

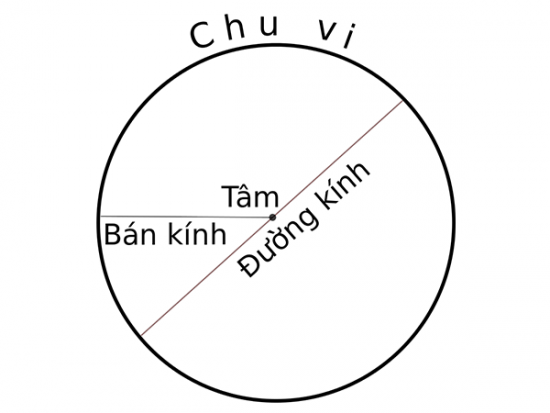
Chúng ta hiểu một cách đơn giản nhất về đường kính hình tròn đó chính là khoảng cách lớn nhất giữa hai điểm bất kì nằm trên đường tròn tròn đó.

Bài viết này được đăng tại [free tuts .net]

Hoặc đường kính là độ dài của đường thẳng đi qua tâm của hình tròn.

2. Cách tính đường kính hình tròn

Chúng ta có thể dựa vào những dữ liệu bài toán đã cho để tìm được đường kính của hình tròn đó.

Thông thường chúng ta sẽ dựa vào các chỉ số bán kính (kí hiệu r), diện tích (kí hiệu S), chu vi (kí hiệu C) và chỉ số PI (3,14).

Cách tìm đường kính hình tròn khi biết bán kính

Đối với trường hợp tìm đường kính của hình tròn khi biết bán kính của hình tròn đó chúng ta có cách tính như sau: Đường kính hình tròn bằng hai lần bán kính

 d = 2 x r

Ví dụ: Cho hình tròn tâm O có bán kính băng 2cm. Tìm đường kính của hình tròn đó?

Ta đã biết bán kính rồi nên dễ dàng tìm được đường kính qua công thức đã học.

Vậy đường kính của hình tròn đó là:

d = 2 x 2=4(cm)
Đáp số: 4(cm)

Cách tìm đường kính hình tròn khi biết chu vi

Như chúng ta đã quy định trước đó thì gọi:

• C là chu vi hình tròn
• d là đường kính của hình tròn
• Pi là chỉ số có giá trị bằng 3,14

Từ công thức tính chu vi:

C = d x 3,14

Chúng ta có thể suy ra công thức tính đường kính hình tròn đó là: Muốn tìm đường kính hình tròn ta lấy chu vi chia cho Pi.

d = C ÷ 3,14

Ví dụ: Cho hình tròn tâm O có chu vi bằng 15,7cm. Tìm đường kính của hình tròn đó?

Áp dụng công thức, ta tính được đường kính của hình tròn đó là:

d = 15,7 ÷ 3,14 = 5(cm)
Đáp số: 5 cm

Cách tìm đường kính hình tròn khi biết diện tích của hình tròn đó

Trước đó chúng ta đã biết được cách tính diện tích của hình tròn đó là

 S = r2 x 3,14

Vậy dựa vào công thức tính diện tích chúng ta có thể đi tìm được bán kính của hình tròn đó:

Từ đó chúng ta có thể suy ra được công thức tìm đường kính của hình tròn khi biết diện tích của hình tròn đó như sau:

Ví dụ: Cho một hình tròn tâm O có diện tích là 12,56 cm². Tìm đường kính của hình tròn đó?

Áp dụng công thức trên ta tính được đường kính của hình tròn đó là:

Đáp số: 4 cm

Trên đây là tổng hợp các cách tìm đường kính hình tròn cơ bản và dễ hiểu nhất giúp các bạn áp dụng vào thực hành. Các bạn hãy áp dụng chính xác vào mỗi đề bài mà bài toán đưa ra nhé. Chúc các bạn thành công.