Hai dạng bài tập thường gặp về hình bình hành

Bài này mình sẽ chia sẻ hai dạng bài tập thường gặp về hình bình hành trong toán học.

Nếu bạn đang là học sinh trung học thì hãy luôn ghi nhớ hai dạng bài tập dưới đây nhé, đó là vận dụng tính chất của hình bình hành để chứng minh các bài toán hình học, và chứng minh một hình tức giác là hình bình hành dựa vào dấu hiệu nhận biết.

1. Vận dụng tính chất của hình bình hành để chứng minh các bài toán hình học

Đối với dạng toán này chúng ta cần vận dụng các tính chất của hình bình hành một cách linh hoạt.

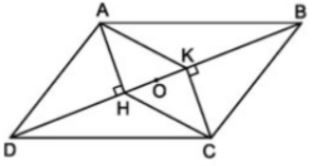
Ví dụ 1: Cho hình bình hành ABCD như hình vẽ. Có H và K lần lượt là đường cao của tam giác ADB và tam giác BCD. Hãy chứng minh tứ giác AHCK là hình bình hành?

Bài viết này được đăng tại [free tuts .net]

Giải:

Từ đề bài đặt ra chúng ta có:

• AH vuông góc với BD
• CK vuông góc với BD

Nên chúng ta suy ra được AH // CK (1)

Dựa theo đề bài thì ABCD là hình bình hành và tính chất của hình bình hành nên chúng ta lại có:

• Cạnh AD = BC
• Góc D = góc B
• Góc H = góc K = 90 độ

Từ các dữ liệu trên chúng ta biết được tam giác ADH = tam giác BCK

Suy ra cạnh AH = CK (2)

Từ (1) và (2) chúng ta kết luận rằng tứ giác AHCK là hình bình hành vì tứ giác này có cặp cạnh đối song song và bằng nhau.

Ví dụ 2: Cho tứ giác ABCD là hình bình hành. Kẻ đoạn thẳng AE vuông góc với BD và đoạn thẳng CF vuông góc với BD. Chứng minh tứ giác AFCE là hình bình hành.

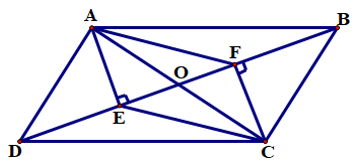
Giải:

Ta có tứ giác ABCD là hình bình hành, gọi O là giao điểm của hai đường chéo AC và BD, suy ra OA = OC (1)

Xét tam giác vuông AEO và tam giác vuông CFO ta có:

• Góc E = F = 90 độ, mà theo dữ liệu (1) chúng ta có OA=OC

Do đó tam giác AEO = tam giác CFO ( cạnh huyền- góc nhọn), suy ra OE = OF (2)

Từ (1) và (2) chúng ta kết luận rằng tứ giác AFCE là hình bình hành vì tứ giác này có hai đường chéo cắt nhau tại trung điểm của mỗi đường

2. Chứng minh một hình tứ giác là hình bình hành dựa vào dấu hiệu nhận biết

Ví dụ: Cho tứ giác IKLM và có các góc đối bằng nhau. Hãy chứng minh rằng tứ giác đó là hình bình hành.

Giải:

Vì tổng 4 góc của một hình tứ giác bằng 360 độ nên:

• Tứ giác IKLM có góc I+ góc K+ góc L+ góc M=360 độ

Mà:

• Góc I = góc L
• Góc K = góc M
• 2I + 2K= 360 độ

I + K = 180 độ, mà chúng ở vị trí trên cùng một phía nên IK // ML(1)

Tương tự như thế ta chứng minh

• 2I + 2K = 360 độ

I + M = 180 độ, mà chúng ở cùng một phía nên IK // ML(2)

Từ (1) và (2), chúng ta kết luận rằng tứ giác IKLM là hình bình hành

Trên đây là các dạng bài tập và một số ví dụ về các bài toán về hình bình hành. Các bạn tham khảo và áp dụng thật tốt vào học tập nhé. Chúc các bạn thành công.