Định lý Talet và các hệ quả trong tam giác (định lý talet đảo)

Bài này sẽ phân tích định lý talet và các tính chất của nó, đồng thời giúp bạn hiểu về định lý talet đảo.

Xin chào các bạn học sinh thân mến, các bạn đã biết gì về định lý Talet? Cách để sử dụng định lý Talet trong hình học như thế nào chưa? Bài viết này chúng ta cùng nhau giải quyết những thắc mắc trên nhé.

1. Định lí talet trong hình tam giác

Định lí Talet trong tam giác được phát biểu một cách khái quát như sau:

Nếu có một đường thẳng song song với một cạnh nào đó của hình tam giác và cắt hai cạnh còn lại của hình tam giác thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Bài viết này được đăng tại [free tuts .net]

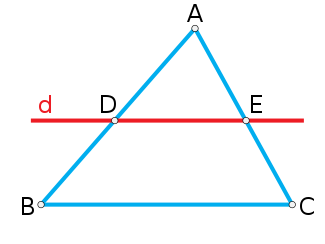
Ví dụ: Cho hình như bên dưới, ta có tam giác ABC và hai cạnh DE // BC. Vậy:

(!! => \frac{AD}{AB} = \frac{AE}{AC} và \frac{AD}{BD} = \frac{AE}{EC} !!)

Ngoài định lí trên thì chúng ta còn biết đến và áp dụng định lí Talet đảo. Định lí này được phát biểu như sau:

Nếu một đường thẳng cắt hai cạnh của một hình tam giác và định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì đoạn thẳng đó song song với cạnh còn lại của hình tam giác

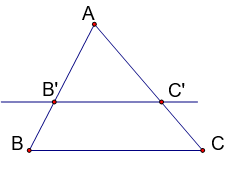
Ví dụ: Tam giác ABC có:

(!! \frac{AB'}{B'B} = \frac{AC'}{C'C} => B'C' // BC !!)

Ví dụ: Cho hình tam giác ABC như hình vẽ, Tính đoạn thẳng X thông qua các chỉ số đã cho như trên hình?

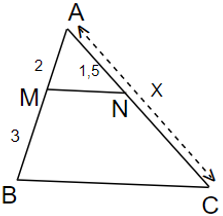
Giải:

Áp dụng định lí Talet, ta có: MN // BC

(!! \frac{AM}{AB} = \frac{AN}{AC} !!)

(!! <=> \frac{2}{5} = \frac{1,5}{X} !!)

(!! => X = 3.75 !!)

Vậy đoạn thẳng X cần tìm là 3.75

2. Hệ quả của định lí Talet

Ngoài những định lí Talet trong hình tam giác thì chúng còn có những hệ quả sau:

• Hệ quả thứ nhất: Khi một đường thẳng cắt hai cạnh của một hình tam giác và song song với cạnh còn lại thì nó sẽ tạo thành một hình tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho
• Hệ quả thứ hai: Khi một đường thẳng cắt hai cạnh của một hình tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu
• Hệ quả thứ ba: Nếu ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tương ứng tỉ lệ

3. Định lí Talet trong hình thang

Trong hình thang định lí Talet được phát biểu như sau:

Nếu có một đường thẳng song song với hai cạnh đáy của hình thang và cắt hai cạnh bên của hình thì thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ

Trong thực tế, các nhà kĩ sư, thiết kế cũng đã vận dụng định lí Talet một cách thành công vào việc đo khoảng cách giữa hai bờ sông mà không cần sang sông, từ đó có thể xây dựng những cây cầu một cách đơn giản hơn

Thông qua bài viết này hi vọng sẽ giúp các em áp dụng được vào cách giải các bài toán liên quan nhé.