Công thức tính diện tích và thể tích hình nón và hình nón cụt

Trong bài này mình sẽ tổng hợp các công thức tính diện tích toàn phần, công thức diện tích xung quanh, và công thức tính thể tính hình nón nhé.

Hình nón là một dạng hình học tương đối khó đối với học sinh trung học. Nếu bài toán ra đủ thông tin dễ giải, nhưng có một số bài toán sẽ áp dụng nhiều công thức khác nữa. Vì vậy, bạn cần nắm vững khái niệm và công thức riêng của nó để áp dụng vào giải các dạng bài tập nhé.

1. Hình nón là gì?

Khi chúng ta quay một tam giác vuông một vòng quanh một cạnh góc vuông cố định thì chúng ta có hình nón.

Trong cuộc sống chúng ta thường xuyên bắt gặp hình nón thông qua chiếc nón, là biểu tượng của phụ nữ Việt.

Bài viết này được đăng tại [free tuts .net]

Hình nón được chia ra thành hai loại đó là hình nón và hình nón cụt.

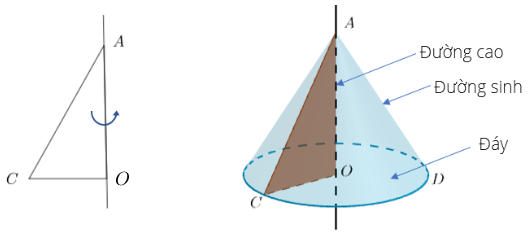
Khi quay một vòng tam giác vuông AOC xung quanh cạnh góc vuông AO thì chúng ta có:

• Đáy của hình nón chính là cạnh góc vuông OC tạo nên một hình tròn
• Cạnh huyền AC vẽ nên mặt xung quanh của hình tròn đáy
• Đường sinh chính là mỗi vị trí của AC
• Đỉnh của hình nón chính là điểm A
• Đường cao của hình nón chính là cạnh AO

Công thức tính diện tích xung quanh của hình nón

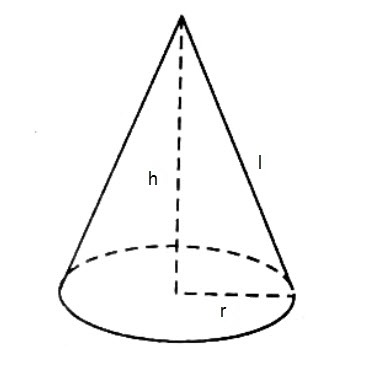
Diện tích xung quanh của hình nón chính là phần diện tích bao quanh hình nón, không tính mặt đáy.

Diện tích hình nón sẽ là tích của Pi với bán kính mặt đáy và đường sinh của hình nón đó.

Công thức tổng quát:

(!! Sxq= \pi \times r \times l !!)

Trong đó:

• Sxq là diện tích xung quanh
• r là bán kính mặt đáy
• l là đường sinh của hình nón

Công thức tính diện tích toàn phần của hình nón

Diện tích toàn phần của hình nón chính là tổng diện tích xung quanh của hình nón với diện tích mặt đáy của hình nón đó.

Công thức tổng quát:

(!! Stp= Sxq+ S đáy !!)

Trong đó diện tích đáy được tính bằng công thức sau:

(!! Sđáy= \pi \times r^2 !!)

Như các bạn thấy, đó là công thức tính hình tròn, bởi mặt đấy là một hình tròn.

Công thức tính thể tích của hình nón

Phần không gian mà hình nón chiếm phải được gọi là thể tích hình nón.

Muốn tính thể tích hình nón chúng ta sẽ sử dụng công thức sau:

(!! V= \frac{\pi \times r^2 \times h}{3} !!)

Trong đó:

• V là thể tích hình nón
• r là bán kính mặt đáy
• h là chiều cao của hình nón

2. Hình nón cụt là gì?

Hình nón cụt là hình được tạo ra khi hình nón có một mặt phẳng song song với đáy cắt một phần phía đỉnh của nón.

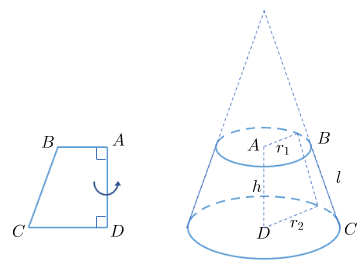
Khi quay hình thang vuôngABCD một vòng quanh cạnh bên vuông góc với hai đáy, ta có:

• Hai cạnh AB và CD tạo nên hai hình tròn có bán kính r1 và r2, đây được gọi là hai đáy của hình nón cụt
• Cạnh CB quét một vòng tạo nên mặt xung quanh của hình nón cụt

Công thức tích xung quanh hình nón cụt

Diện tích xung quanh của hình nón cụt chính là phần diện tích bao quanh hình nón cụt không tính phần diện tích đáy.

Công thức tổng quát:

(!! Sxq= \pi \times (r1+r2) \times l !!)

Trong đó: r1, r2 là bán kính của hai mặt đáy hình nón

Công thức tích toàn phần hình nón cụt

Phần diện tích xung quang và phần diện tích hai đáy của hình nón cụt chính là diện tích toàn phần của hình nón cụt đó.

Công thức tổng quát:

(!! Stp= Sxq+ S2đáy !!)

Hay:

(!! Stp= (\pi \times (r1+r2) \times l)+ (\pi \times r1^2+ \pi \times r2^2) !!)

Trong đó:

• r1, r2 là bán kính của hai mặt đáy hình nón
• l là đường sinh của hình nón

Công thức tính thể tích của hình nón cụt

Thể tích của hình nón cụt chính là một khoảng không gian mà hình đó chiếm phải.

Chúng ta có cách tính thể tích của hình nón bằng cách lấy thể tích của hình nón lớn trừ đi thể tích của hình nón nhỏ.

Công thức chung:

(!! V= \frac{1}{3} \times (r1^2+r2^2+r1 \times r2) \times h !!)

Trong đó:

• V là thể tích của hình nón cụt
• r1 và r2 là bán kính của hai đáy
• h là chiều cao hình nón cụt

3. Bài tập vận dụng các công thức hình nón, hình nón cụt

Bài tập 1: Cho một hình nón được đặt vào bên trong một hình lập phương (biết cạnh của hình lập phương bằng 1). Các em hãy tính:

• a) Độ dài bán kính của mặt đáy hình nón
• b) Cho biết đường sinh của hình nón dài bao nhiêu?

Bài giải:

a) Vì đường tròn đáy của hình nón nội tiếp trong hình vuông là mặt của hình lập phương đó. Chính vì thế bán kính của hình tròn đáy của hình nón sẽ bằng một nửa cạnh của hình lập phương, bằng 0,5. Vậy bán kính của mặt đáy hình nón là 0,5

b) Chúng ta có đỉnh của hình nón tiếp xúc với một mặt phẳng của hình lập phương, chính vì thế đường cao của hình nón cũng chính là bằng chiều dài một cạnh của hình lập phương, bằng 1.

Áp dụng công thức tính đường sinh của hình nón:

(!! l=\sqrt{h^2 + r^2} !!)

(!! \Leftrightarrow l=\sqrt{1^2 + 0.5^2}=\sqrt{1+\frac{1}{4}}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2} !!)

Vậy ta có độ dài đường sinh là 52.

Bài tập 2: Một hình nón có thiết diện qua trục là tam giác vuông cân có thiết diện bằng 2. Hãy tính diện tích xung quanh của khối nón đó?

Bài giải:

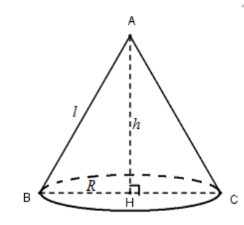
Bởi vì tam giác ABC vuông cân và có diện tích bằng 2 nên:

(!! \frac{1}{2} AC^2=2 !!)

(!! \Leftrightarrow AC=AB=2 !!)

(!! BC=\sqrt{2^2+2^2} =2 \times \sqrt{2} !!)

(!! \Rightarrow h=R=\frac{BC}{2}=\sqrt{2} !!)

Chúng ta có diện tích xung quanh của khối nón đó là:

(!! \pi \times \sqrt{2} \times 2 = 2 \times \sqrt{2 \pi} !!)

Bài toán 3: Cho một hình nón có diện tích xung quanh là 65cm2và bán kính đáy bằng 5cm.

Hãy tính:

1. Diện tích toàn phần của hình nón
2. Thể tích của hình nón
3. Người ta đã cắt hình nón bằng một mặt phẳng (Q) song song với đáy và đi qua trung điểm của đường cao hình nón đó, tạo thành một hình nón cụt. Hãy tính thể tích của hình nón cụt đó?

Bài giải:

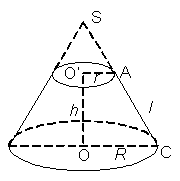
1. Áp dụng công thức tính diện tích đáy của hình nón chúng ta có:

(!! Sđáy=\pi \times r^2= \pi \times 5^2=25 (cm^2) !!)

Diện tích toàn phần của hình nón là:

(!! 65 \pi +25 \pi =90 \pi (cm^2) !!)

2. Dựa vào công thức tính diện tích xung quanh chúng ta suy ra được cách tính đường sinh của hình nón, đó là:

(!! l=\frac{Sxq}{\pi \times r}=\frac{65 \pi}{\pi \times 5}=13 (cm) !!)

Gọi đường cao của hình nón là SO, chúng ta có:

(!! SO=\sqrt{SC^2 - OC^2}=\sqrt{13^2 - 5^2}=12(cm) !!)

Từ đó, chúng ta có thể tích của hình nón là:

(!! \frac{1}{3} \times \pi \times 5^2 \times 12 =100 (cm3) !!)

3. Gọi O’ là trung điểm của SO

Gọi A là giao điểm của SC với mặt phẳng ( Q).

Vì O’A là đường trung bình của tam giác SOC nên O’A bằng 2,5 cm.

Vậy thể tích của hình nón cụt đó sẽ là:

(!! \frac{1}{3} \pi \times 6 \times (5^2 + 2,5^2) + 5 \times 2,5=12,5 (cm^3) !!)

Qua bài này thì các bạn đã biết được cách tính diện tích tích xung quanh và diện tích toàn phần của hình nón và hính nón cụt. Ngoài ra, cách tính thể tích hình nón và hình nón cụt cũng tương đối khó, vì vậy bạn phải làm bài tập thật nhiều thì mới nhớ hết được.