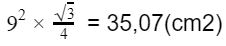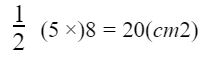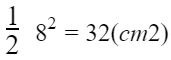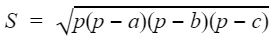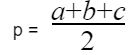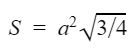Cách tính diện tích hình tam giác (Vuông / Cân / Đều / Thường)

Xin chào tất cả các bạn học sinh thân mến. Hôm nay, mình sẽ hướng dẫn cho các bạn cách tính diện tích hình tam giác dễ hiểu để giúp các bạn có thể thực hiện các bài tập thật tốt nhé.

Chúng ta được biết hình tam giác có nhiều loại, đó là: Tam giác thường, tam giác cân, tam giác đều và tam giác vuông. Chúng ta cùng tìm hiểu sâu về diện tích hình tam giác nào.

I. Hình tam giác là gì?

Hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và có ba cạnh là ba đoạn thẳng nối ba đỉnh với nhau.

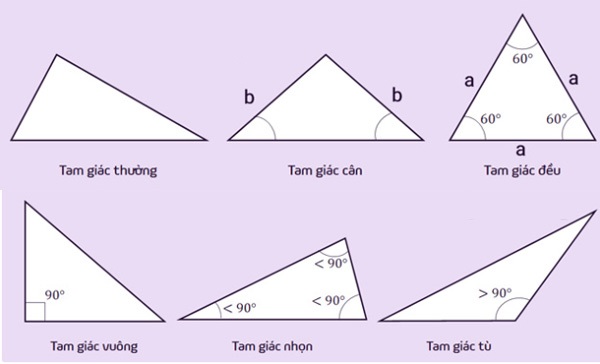
Chiếu theo hình dạng thì chúng ta có các loại hình tác giác gồm: Tam giác thường, tam giác cân, tam giác đều, tam giác vuông, tam giác nhọn, và cuối cùng là tam giác tù.

Bài viết này được đăng tại [free tuts .net]

Chúng ta ẽ có một công thức chuẩn chung để tính diện tích, nhưng mỗi hình đặc biệt cũng sẽ có một công thức riêng giúp bạn tính toán dễ dàng hơn. Sau đây chúng ta cùng tìm hiểu nhé.

II. Các công thức tính diện tích hình tam giác

1. Cách tính diện tích tam giác thường

Đây là loại hình tam giác cơ bản nhất, có độ dài các cạnh khác nhau và số đo các góc cũng khác nhau. Tuy nhiên, tam giác thường cũng có thể được bao gồm các trường hợp đặc biệt của hình tam giác mà mình đã trình bày ở phần I.

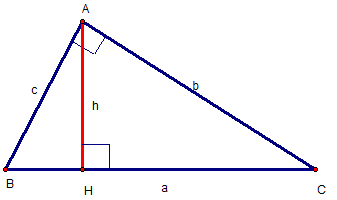
Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

Ta có công thức tổng quát:

(Trong đó S là diện tích, a là độ dài cạnh đáy, h là chiêu cao)

Ví dụ: Cho hình tam giác có độ dài cạnh đáy là 7cm, chiều cao của hình tam giác là 5cm. Tính diện tích của hình tam giác đó?

Giai: Áp dụng công thức tính diện tích của hình tam giác, ta có kết quả như sau:

S = (7x5):2= 13,5 (cm2)

2. Cách tính diện tích tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau. Tương tự như tam giác thường, chúng ta có cách tính diện tích hình tam giác cân:

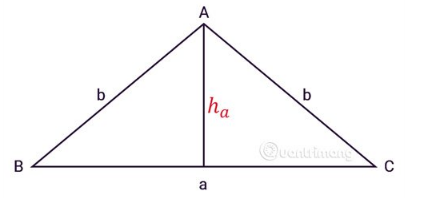
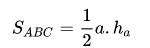
Ví dụ: Cho hình tam giác cân có chiều dài đáy bằng 12 cm, chiều cao của hình tam giác bằng ½ chiều dài đáy. Tính diện tích của hình tam giác đó.

Giai: Chiều cao của hình tam giác là:

h = 12:2 = 6(cm)

Vậy, diện tích của hình tam giác là:

S = (12x6):2 = 36(cm2)

Đáp số: 36 (cm2)

3. Cách tính diện tích tam giác đều

Tam giác đều là tam giác có 3 cạnh bằng nhau. Để tính được diện tích của tam giác đều, chúng ta áp dụng định lý Heron để suy ra công thức tính như sau:

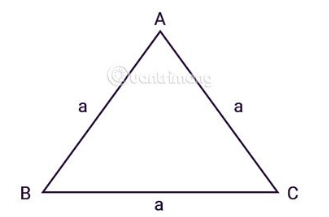
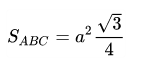
Ví dụ: Cho một tam giác đều có độ dài cạnh bằng 9cm. Tính diện tích của hình tam giác đều đó.

Giai: Áp dụng công thức tính diện tích tam giác đều, ta có kết quả như sau:

Đáp số: 35,07(cm2)

4. Cách tính diện tích hình tam giác vuông

Tam giác vuông là tam giác trong đó có 1 góc là góc vuông( góc 90 độ). Mối quan hệ giữa các cạnh và góc của một tam giác vuông là nền tảng cơ bản của lượng giác học.

Cũng giống như những loại hình tam giác khác, chúng ta cũng có công thức tính diện tích của hình tam giác vuông:

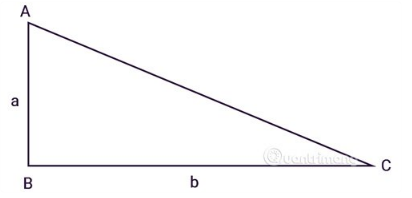
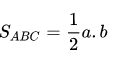
Ví dụ: Cho một tam giác vuông có hai cạnh góc vuông lần lượt là 5cm và 8cm. Tính diện tích của hình tam giác vuông đã cho.

Giải: Diện tích của hình tam giác vuông đó là:

Đáp số: 20(cm2)

5. Cách tính diện tích hình tam giác vuông cân

Tam giác vuông cân vừa là tam giác vuông vừa là tam giác cân. Trong tam giác vuông cân có hai cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45 độ.

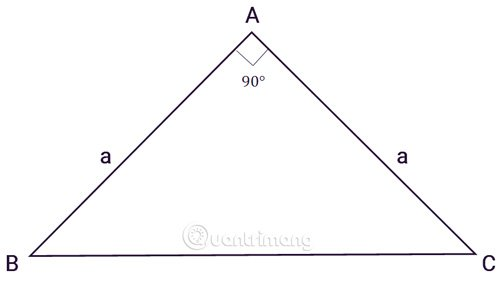
Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:

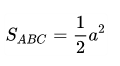
Ví dụ: Cho một hình tam giác vuông cân có độ dài cạnh bằng 8cm. Tính diện tích của hình tam giác đã cho.

Giải:

Diện tích của hình tam giác đó là:

Đáp số: 32(cm2)

III. Các câu hỏi thường gặp liên quan đến diện tích hình tam giác

1. Tính diện tích tam giác khi biết 3 cạnh theo định lý heron

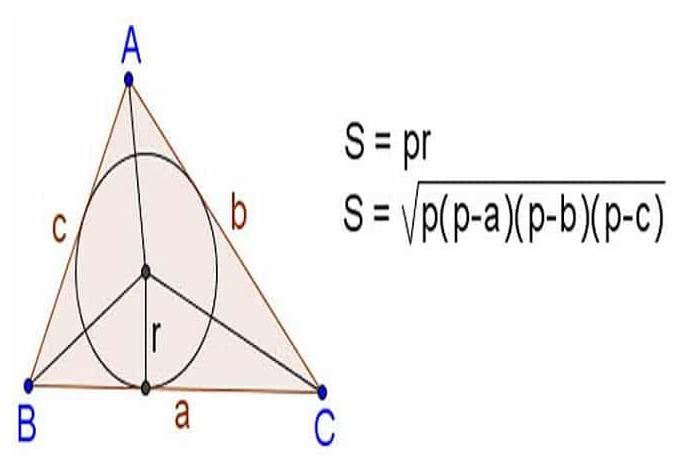
Gọi S là diện tích của hình tam giác và a,b,c lần lượt là cạnh của hình tam giác đó.

Công thức Heron được viết như sau :

Trong đó p là chu vi của nửa tam giác.

Đối với cách tính này thì các bạn học sinh cần lưu ý khi tìm chu vi nửa hình tam giác nhé, vì đây là yếu tố quan trọng để tính diện tích hình tam giác. Muốn tính được chu vi nửa hình tam giác chúng ta có công thức sau

Ví dụ: Cho độ dài của 3 cạnh tam giác lần lượt là 7cm, 8cm và 9cm. Tìm diện tích của hình tam giác đó.

Giai:

Chu vi của hình tam giác đó là:

p = (7+8+9):2=12(cm)

Diện tích của hình tam giác đó là:

Đáp số: 26,83(cm2)

2. Cách tính diện tích tam giác đều cạnh 2a

Đối với bài toán tính diện tích hình tam giác đều mà bài toán chỉ cho biết một cạnh thì các bạn áp dụng công thức sau đây:

Trong đó a là độ dài cạnh của hình tam giác đều

Trên đây là tổng hợp cách tính diện tích hình tam giác, hy vọng bài viết sẽ giúp các bạn tìm ra cách giải các bài tập liên quan thật tốt. Chúc các bạn thành công.