Công thức tính thể tích khối tứ diện đều cạnh a và bài tập

Công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3, 2a và một số dạng bài tập liên quan cùng hướng dẫn giải chi tiết nhất, tham khảo tại đây.

Khối tứ diện đều là một phần kiến thức rất quan trọng và thường xuyên xuất hiện trong các bài thi THPT Quốc Gia. Trong đó, thể tích khối tứ diện đều là một nội dung không thể nào bỏ qua được, hiểu được vấn đề này trong bài viết hôm nay, freetuts sẽ chia sẻ tới cho các em các kiến thức liên quan đến tính thể tích của khối tứ diện đều và một số bài tập liên quan để các em có thể ôn luyện nội dung này thật tốt.

Khối tứ diện đều là gì?

Trong hình học không gian, khối tứ diện đều hay còn gọi là hình chóp tam giác đều là một khối đa diện có 4 mặt là 4 tam giác đều và có 2 tính chất cơ bản sau.

• Tất cả các mặt của tứ diện đều là các tam giác đều có diện tích bằng nhau.
• Tất cả các cạnh của tứ diện đều thì có độ dài bằng nhau.

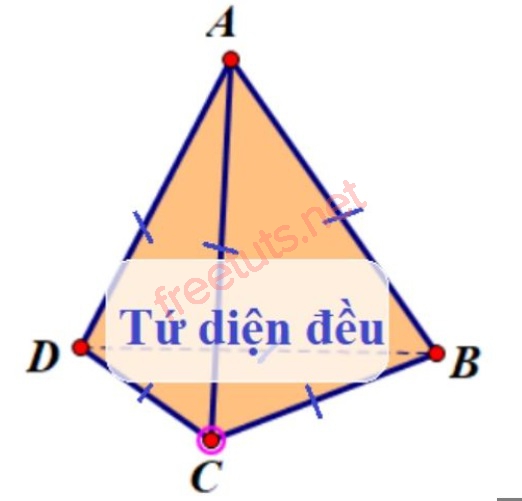
Ví dụ về khối tứ diện đều ABCD.

Công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3

Để tính thể tích của khối tứ diện đều có các cạnh là a, a, a√2, a√3, 2a, các em hãy làm theo hướng dẫn sau:

Bài viết này được đăng tại [free tuts .net]

Thể tích khối tứ diện đều cạnh a

Cho tứ diện đều ABCD, có độ dài các cạnh bằng nhau và bằng a, tính thể tích khối tứ diện ABCD.

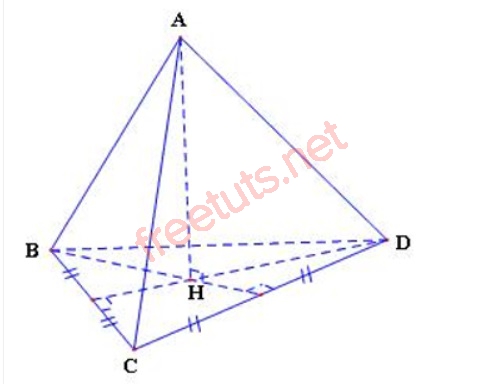
Hình ảnh minh họa tứ diện đều ABCD.

Lời giải:

Ta có diện tích tam giác đều BCD cạnh a là:

S(BCD) = (a^2.a√3)/4

Gọi H là trọng tâm tam giác BCD nên AH vuông góc với (BCD)

Xét tam giác vuông ABH, có:

AH = √(AB^2 - BH^2) = (a√6)/3

Vậy thể tích của khối tứ diện đều cạnh a là:

V(ABCD) = 1/3 . S(BCD).AH = ⅓. (a^2√3)/4.(a√6)/3 = (a^3√2)/12

Công thức như sau:

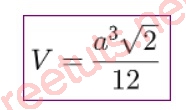
Thể tích khối tứ diện đều cạnh a√2

Với khối tứ diện đều có cạnh là a√2, thế a√2 vào công thức trên ta có:

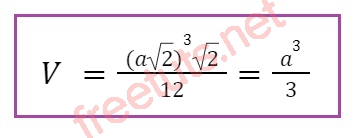
Thể tích khối tứ diện đều cạnh a√3

Với khối tứ diện đều có cạnh là a√3, thế a√3 vào công thức trên ta có:

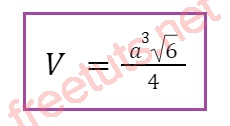
Thể tích khối tứ diện đều cạnh 2a

Với khối tứ diện đều có cạnh là 2a, thế 2a vào công thức trên ta có:

Lưu ý khi tinh thể tích khối tứ diện đều

Muốn giải được các bài toán tính thể tích cùa một khối tứ diện đều, điều quan trọng mà các em cần lưu ý đó là cách vẽ tứ diện đều sao cho chính xác. Hãy tham khảo các bước mà freetuts đã liệt kê dưới đây nha:

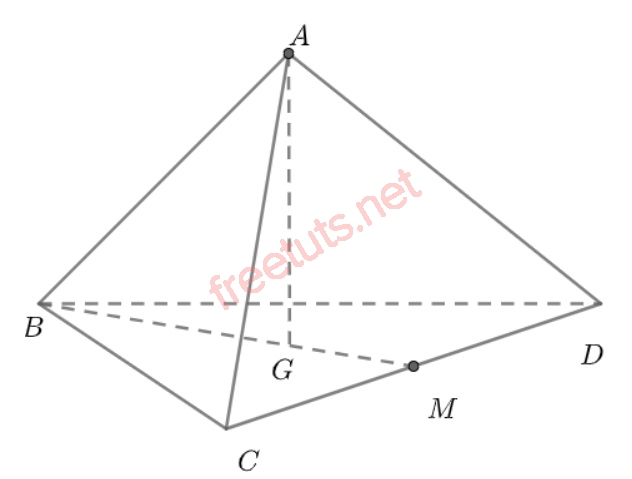
Cách vẽ hình tứ diện đều ABCD.

Coi hình tứ diện này là hình chóp tam giác đều. Vi dụ A.BCD

• Trong mặt đáy (BCD), vẽ đường trung tuyến BM, vậy BM là trung tuyến của tam giác BCD.
• Xác định điểm trọng tâm G của tam giác BCD, và G cũng chính là tâm của đáy.
• Dựng đường cao đi qua G song song với mép vở.
• Trên đường cao vừa dựng, xác định điểm A, nối A với 3 điểm B, C, D là chúng ta đã hoàn thiện được hình chóp đều ABCD.

Bài tập tính thể tích khối tứ diện đều

Bài 1: Cho tứ diện ABCD, có ABC, ABD là 2 tam giác đều cạnh a, ACD vuông góc với BCD.

a. Tính thể tích khối tứ diện ABCD theo a.

b. Tính so đo góc giữa 2 đường thẳng AD và BC

Lời giải:

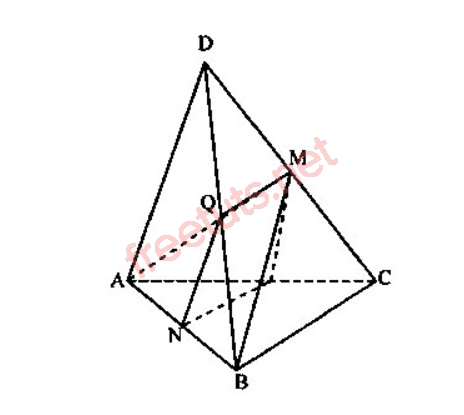
Gọi M là trung điểm CD, Q là trung điểm của DB, lúc này, ta có AM vuông góc với CD, BM vuông góc với CD.

Theo đề bài, ta có: góc AMB bằng 90 độ.

Xét tam giác AMB ta có:

AM = BM, góc AMB bằng 90 độ, nên suy ra tam giac AMB vuông cân tại M.

Suy ra:

Cạnh BM = (a√2)/2.

Vì M là trung điểm CD nên CD = 2CM = 2√(BC^2 - BM^2) = a√2

Vậy, thể tích tứ diện ABCD là:

V(ABC) = 1/3.CD.S(ABM) = 1/6.CD.AM.BM = (a^3√2)/12.

b. Gọi N, P, Q lần lượt là trung điểm của 3 cạnh AB, AC và BD.

Ta có:

Góc tạo bởi hai đường chéo AD và BC = góc tạo bởi 2 đường chéo NP và MP.

Xét tam giác AMB vuông cân tại M, nên suy ra:

MN = AB/2 = a/2 = NP = PM.

Xét tam giác MNP có MN = NP = PM, nên suy ra tam giác MNP là tam giác đều.

Vậy góc MPN = 60 độ, nên Góc tạo bởi hai đường chéo AD và BC = 60 độ.

Bài 2: Cho tứ diện đều ABCD, Gọi (M) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều ABCD. Tính tỉ số V(M)/V(ABCD)

Lời giải:

Gọi cạnh của tứ diện đều ABCD có độ dài bằng a, thì cạnh của bát diện đều (M) là a/2.

Lúc này ta có

V(ABCD) = a^3(√2/12), V(M) = 1/3.(a/2)^3√2 = (a^3√2)/24

Từ đó suy ra: V(H)/V(ABCD) = 1/2

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ cho các em chi tiết các công thức tính thể tích khối tứ diện đều cạnh a, a√2, a√3, 2a và một số bài tập liên quan. Hy vọng đây sẽ là những kiến thức bổ ích cho các bạn học sinh THPT. Chúc các em học tập tốt, đạt kết quả cao.