Định lý cosin, các hệ quả quan trọng và bài tập áp dụng

Định lý cosin trong một tam giác được hiểu như sau, bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trừ đi 2 lần tích 2 cạnh với cosin góc xen giữa.

Trong toán học, định lý cosin là một trong những kiến thức vô cùng quan trọng, là nền móng cơ bản để cho các em ứng dụng vào những bài toán trong suốt quãng thời gian học. Tuy nhiên, hiện có rất nhiều bạn còn mơ hồ về định lý cos, vì vậy, trong bài viết hôm nay, hãy cùng freetuts ôn tập lại những kiến thức liên quan tới định lý cosin và những hệ quả quan trọng của định lý này nhé.

Lý thuyết định lý cosin

Trong lượng giác, định lý cosin (định lý cos) là khái niệm biểu diễn cho sự liên quan giữa chiều dài các cạnh của một tam giác với cosin của góc tương ứng với nó và được phát biểu định lý sin bằng lời như sau:

Trong một tam giác, bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trừ đi 2 lần tích của 2 cạnh này với cosin của góc xen giữa chúng.

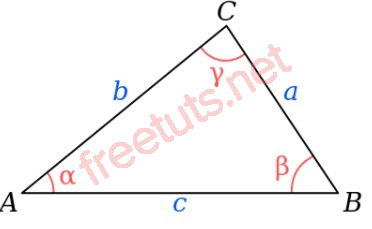
Cho tam giác ABC như hình, có độ dành 3 cạnh lần lượt là: AB = c, BC = a, AC = b.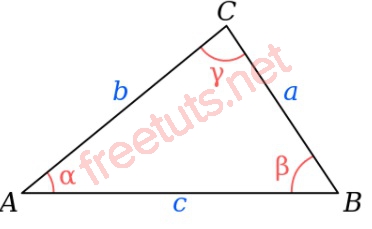

Theo định lý cos, ta có:

Bài viết này được đăng tại [free tuts .net]

a2 = b2 + c2 - 2bc.cosα

b2 = a2 + c2 - 2ac.cosβ

c2 = a2 + b2 - 2ab.cosγ

Như vậy, nếu trong một tam giác, biết độ dài 2 cạnh và góc xen giữa, chúng ta có thể tính độ dài của cạnh còn lại.

Hệ quả định lý cosin và ứng dụng trong lượng giác

Trong lượng giác, định lý cos có ứng dụng vô cùng quan trọng, vì nhờ có định lý này mà bạn có thể giải được một tam giác hoặc đường tròn bất kỳ như sau:

Tính cạnh còn lại của tam giác

Dựa vào định lý cos, khi biết độ dài hai cạnh (a,b) và góc xen giữa chúng , ta có thể dễ dàng tìm được độ dành cạnh còn lại nhờ công thức sau:

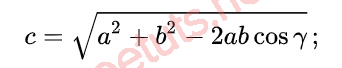
Nếu bạn biết độ dài 2 cạnh và góc đối diện một trong hai cạnh đó, hãy áp dụng công thức sau để tính độ dài cạnh còn lại nha.

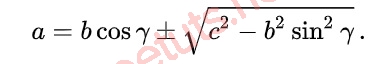
Áp dụng định lý cosin tính góc 3 góc của tam giác

Khi biết độ dài 3 cạnh a, b, c của một tam giác bất kỳ, chúng ta có thể tính số đo 3 góc lần của tam giác này với công thức sau:

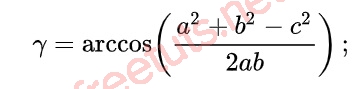
Tính diện tích tam giác

Cho tam giác ABC, trong đó ha,hb,hc lần lượt là độ dài đường cao kẻ từ 3 đỉnh A, B, C. Độ dài 3 cạnh tương ứng là a, b, c.

Lúc này, ta sẽ có các công thức tính diện tích tam giác như sau:

S = 1/2.BC.ha = 1/2AC.hb = ½ AB.hc

S = 1/2ab.sinC = 1/2ac.sinB = 1/2bc.sinA

S = (abc)/(4R)

Trong đó:

• R là bán kính đường tròn ngoại tiếp tam giác ABC.

S = pr

Trong đó:

• r là bán kính đường tròn nội tiếp

• p = (a + b + c)/2

Cách chứng minh định lý cosin lớp 9 là đúng

Cho tam giác ABC, lần lượt có độ dài 3 cạnh là a, b, c, góc là góc đối diện cạnh c và để chứng minh định lý hàm cosin là đúng, các bạn có thể áp dụng các phương pháp mà freetuts đã liệt kê dưới đây để chứng minh:

Xét tam giác ABC, có tọa độ 3 đỉnh lần lượt là A(bcosγ, bsinγ), B(a,0), C(0,0).

Sử dụng công thức tính khoảng cách để chứng minh

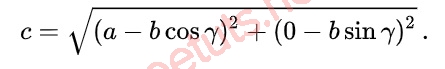
Ta được:

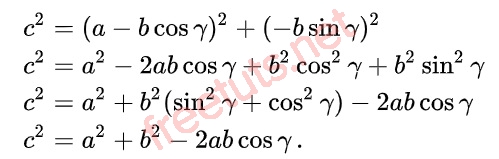
Vậy định lý cos là đúng.

Sử dụng công thức lượng giác để chứng minh

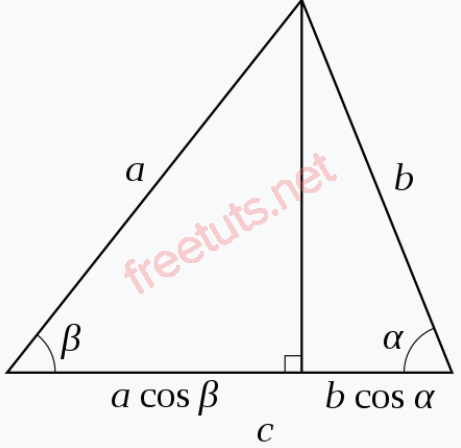
Vẽ đường cao tương ứng với cạnh c như hình trên, lúc này ta có:

c = a.cosβ + b.cosβ.

Nhân hai vế với c, ta được:

c² = ac.cosβ + bc.cosβ

b² = bc.cosα + ab.cosα

a² = ac.cosγ + ab.cosγ

Lấy a² + b² = ac.cosβ + bc.cosα + 2ab.cosγ

a² + b² - c² = ac.cosβ + bc.cosα + 2ab.cosγ - ac.cosβ + bc.cosβ

a² + b² - c² = 2ab.cosγ

c² = a² + b² - 2ab.cosγ

Như vậy, chúng ta đã chứng minh được định lý cosin là đúng.

Sử dụng định lý Pytago để chứng minh

Trong trường hợp tam giác tù, ta có thể chứng minh định lý cos đúng bằng cách áp dụng Định lý Pytago như sau:

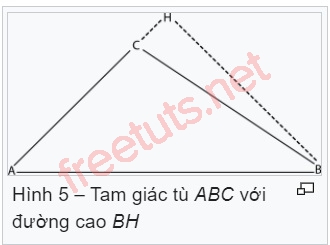
Kẻ đường thẳng BH vuông góc với cạnh AC, lúc này BH cũng chính là đường cao của tam giác tù ABC.

Gọi chiều dài cạnh CH = d, BH = h, xét tam giác vuông ABH, ta có:

c² = (b + d)² + h² = b² + 2bd + (d² + h²)

Xét tam giác vuông CHB, ta có:

d² + h² = a², thế vào biểu thức trên, ta có:

c² = a² + b² + 2bd (1)

Theo mệnh đề 12 của Euclid, ta có:

d = a.cos( π - γ) = -a.cosγ, thế vào (1), ta có:

c² = a² + b² + 2bd ⇔ c² = a² + b² - 2ab.cosγ, vậy định lý cos là đúng.

Bài tập về định lý cosin

Sau khi đã nắm vững lý thuyết về định lý hàm số cosin, bây giờ các em hãy vận dụng những kiến thức trên để giải một số bài tập sau đây nhé:

Bài 1: Cho tam giác ABC như hình, biết độ dài 3 cạnh lần lượt là a = 3 mm, b = 5mm, c = 6mm, hãy tính số đo 3 góc A, B và C.

Lời giải:

Áp dụng hệ quả định lý cos, ta có:

γ = arccos((a² + b² - c²)/(2ab)) = arccos(4² + 5² - 6²)/(2.4.5) = arccos(5/40) ≈ 82 độ.

β = arccos((a² + c² - b²)/(2ac)) = arccos(4² + 6² - 5²)/(2.4.6) = arccos(27/48) ≈ 55 độ.

Xét tam giác ABC, có: α + β + γ = 180 độ ⟹ α = 180 - γ - β = 180 - 82 - 55 = 43 độ.

Vậy tam giác ABC, có số đo góc A = 43 độ, góc B = 55 độ, góc C = 82 độ.

Bài 2: Cho tam giác ABC, biết góc B = 60 độ, BC = 8cm, AB = 5 cm. Tính độ dài cạnh AC và góc A, C.

Lời giải:

Đặt độ dài BC = a, AC = b, AB = c, áp dụng định lý cosin, ta có:

AC² = b² = a² + c² - 2ac.cosB = 8² + 5² - 2.8.5.cos60 = 49

AC = căn bậc 2 của 49 = 7.

Áp dụng hệ quả định lý cos, ta có:

Góc A = arccos((b² + a² - c²)/(2ab)) = arccos(7² + 5² - 8²)/(2.7.5) = arccos(1/7) ≈ 81 độ.

Góc C = 180 - góc A - góc B = 180 - 81 - 49 = 38 độ.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ các kiến thức liên quan đến định lý cosin và hệ quả quan trọng của nó, hy vọng qua bài viết này, các em có thể củng cố lại được kiến thức của mình để có thể hoàn thành tốt các bài kiểm tra sắp tới nhé. Chào tạm biệt và hẹn gặp lại các em trong các bài viết tiếp theo để khám phá thêm nhiều môn học thú vị khác nha.