Số phức là gì? Tính chất, cách tính và tổng hợp bài tập

Lý thuyết về số phức và các khái niệm liên quan cùng các tính chất quan trọng và các dạng bài tập cơ bản thường gặp, mời các em theo dõi tại đây.

Số phức là một kiến thức quan trọng trong chương trình toán lớp 12 và thường xuyên xuất hiện trong các bài thi THPT Quốc gia, chính vì thế các em cần phải nắm vững lý thuyết và các dạng bài tập liên quan. Ngay trong bài viết này, freetuts đã tổng hợp đầy đủ các kiến thức liên quan đến số phức, mời các em cùng xem và tham khảo nhé.

Số phức và các khái niệm liên quan trong toán học

Cùng tìm hiểu lý thuyết số phức và các khái niệm khác liên quan ngay bên dưới đây nhé.

Khái niệm số phức trong toán học

Trong toán học, số phức là số được viết dưới dạng a + bi.

Bài viết này được đăng tại [free tuts .net]

Với:

• a, b là số thực.
• i là một đơn vị ảo, thỏa điều kiện i^2 = -1
• a là phần thực, b là phần ảo của số phức.

Ngoài ra, số phức có thể được biểu diễn trên mặt phẳng phức với trục hoành Oy là trục số thực, trục tung Ox là trục số ảo. Và trong trường hợp này, a + bi được xác định dựa vào điểm A(a,b).

Cho 2 số phức z = a + bi và z’ = a’ + b’i, điều kiện z = z’ a = a’ và b = b’.

Mặt phẳng phức

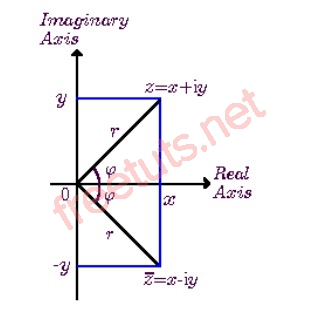
Cho hệ tọa độ Descartes, trục hoành đại diện tọa độ phần thực, trục tung sẽ đại diện cho tọa độ phần ảo, lúc này số phức được biểu diễn dưới dạng:

z = x + i.y

Lúc này, mặt phẳng tọa độ này sẽ được gọi là mặt phẳng phức.

Số phức liên hợp

Cho số phức dưới dạng Z = a + bi, Z ‘ = a - bi được gọi là số phức liên hợp của Z và có tính chất như sau:

Z x Z’ = a^2 + b^2 là một số thực.

Z + Z’ = 2a là một số thực

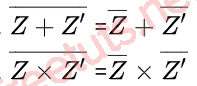
Số phức nghịch đảo

Số phức nghịch đảo hay là nghịch đảo của số phức Z có ký hiệu là Z-1 là số phức có dạng sao cho tích của nó với Z bằng 1.

Số phức nghịch đảo của Z = a + bi là Z-1=1Z=1a+bi=Z|Z2|

Số phức thuần ảo

Một số phức được gọi là thuần ảo khi phần số thực a = 0, suy ra Z = bi thuộc R.

Số phức đối

Theo cách hiểu đơn giản nhất, số phức đối là sự chuyển đổi âm thành dương và ngược lại dương thành âm của một số phức bất kỳ.

Ví dụ: Cho z = a + bi, thì số phức đối của z là -z = -a - bi, và z + (-z) = (-z) + z = 0

Modun số phức

Cho Z = a + bi, ta có Z x Z = a2+b2, và lúc này, căn bậc hai của Z x Z được gọi là module của số phức Z, ký hiệu là |Z|.

|Z2|=a2+b2.

Ta có tính chất của modun như sau:

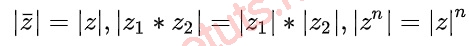
Argument số phức

Trên mặt phẳng tọa độ bằng điểm M(a, b), góc tạo giữa chiều dương của trục Ox và OM được gọi là argument của số phức Z, có ký hiệu là arg(z).

Ta có tính chất của argument như sau:

Dạng đại số và dạng lượng giác của số phức

Số phức đại số

Trong trường số phức, đơn vị ảo i sẽ có tính chất như sau:

i2 =-1 i = -1

Và Z = a + bi, với a, b là các số thực được gọi là dạng lượng giác của Z.

Số phức lượng giác

Ngoài dạng đại số, Z = a + bi có thể viết dưới dạng sau:

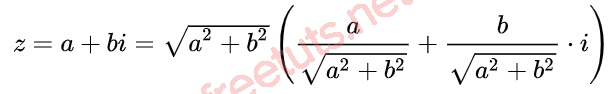
Đặt r = |z|, = arg(z), ta có:

z = r (cos + i.sin), đây được gọi là dạng lượng giác của số phức z.

Trong đó:

• r là số thực.
• là góc.
• r.cos = a là phần thực.
• rsin = b là phần ảo.

Gọi Z(r.cos; rsin), góc tạo bởi OZ và Ox là:

arctan(Zy/Zx) = arctan(rsin/r.cos) = arctan(tan) =

Ví dụ minh họa:

Cho z1 = 2 + 2i, vậy dạng lượng giác của z1 là:

r = 22+22=22.

= arctan(2/2) = /4

Thế vào phương trình ta có:

z1 = 22 (cos/4 +i.sin(/4))

Các phép toán về số phức trong toán học

Trong số phức, cũng có các phép toán cộng, trừ, nhân chia thông thường như số tự nhiên.

Cộng trừ hai số phức

Cho 2 số phức z1 = a1 + b1.i và z2 = a2 + b2.i, ta có:

w = z1 + z2 = (a1 + a2) +(b1 + b2)i

u = z1 - z2 = (a1 - a2) +(b1 - b2)i

Và trong phép cộng hai số phức cũng có đầy đủ các tính chất như phép cộng giữa hai số thực bao gồm:

Tính chất giao hoán: z1 + z2 = z2 + z1, với mọi z1, z2 thuộc C.

Tính chất kết hợp: (z1 + z2) + z3 = z1 + (z2 + z3), với mọi z1, z2 thuộc C.

Ví dụ minh họa:

Cho z = 3 + 6i, z’ = -2 + 3i, tính z + z’ =?

Lời giải:

Ta có z + z’ = (3 + 6i) + (-2 + 3i) = 3 - 2 + (6 + 3)i = 1 + 9u=i.

Nhân hai số phức

Cho 2 số phức z1 = a1 + b1.i và z2 = a2 + b2.i, ta có:

w = z1.z2 = a1.a2 - b1.b2 + (a1b2 + a2b1)i

Cho số thực k, ta có k(a + bi) = (k + 0i)(a + bi) = ka + kbi.

Phép nhân các số phức cũng có đầy đủ tính chất như phép nhân giữa các số thực, với mọi z1, z2, z3 thuộc C, ta có:

Tính chất giao hoán: z1.z2 = z2.z1

Nhân với 1: 1.z = z.1 = z.

Tính chất kết hợp: (z1z2)z3 = z1(z2.z3)

Tính chất phân phối: z1(z2 + z3) = z1z2 + z1z3.

Ví dụ minh họa:

Phân tích ra thừa số của hàm sau: a^2 + 1

Lời giải:

a^2 + 1 = a^2 - i^2 = (a - i)(a + i)

Phép chia số phức khác 0

Ví dụ minh họa:

Thực hiện phép chia số phức sau: z = (-5 + 6i)/(4 + 3i)

Lời giải:

z = (-5 + 6i)/(4 + 3i) = ((-5 + 6i)(4 - 3i))/((4 + 3i).(4 - 3i) = (-2 + 39i).(4^2 + 3^2) = -2/25 + (39/25)i

Khai căn bậc 2 của số phức

Cho z = x + yi là căn bậc 2 của số phức w = a + bi

z2=w x2 - y2 = a, 2xy = b.

• Nếu w = 0, có duy nhất một giá trị căn bậc 2 là z = 0.
• Nếu w khác 0, có 2 giá trị căn bậc 2 đối nhau.

Tính chất của số phức trong toán học

Sau đây là một số tính chất quan trọng của số phức mà freetuts đã tổng hợp được, mời các em cùng tham khảo nha.

z là số thực z = z

z là số ảo z =- z

z. z = |z|^2

z1+z2= z1 +z2

z1.z2= z1 x z2

z1z2=z1 z2

|z1.z2| = |z1|.|z2|

|z1 + z2| |z1|+|z2|

Cho hai số phức z, z’ được biểu diễn dưới dạng lượng giác như sau:

z = r.(cos + i.sin)

z’ = r’.(cos' + i.sin')

Lúc này, ta có tính chất sau:

z.z’ = r.r’(cos+')+isin(+'))

z/z’ = r/r’(cos-')+isin(-'))

zn=rn(cos.n + isin.n)

Ứng dụng của số phức

Số phức có rất nhiều ứng dụng trong toán học, vật lý như:

• Ứng dụng trong hình học phẳng.
• Phân tích đa thức ra thừa số.
• Tính toán các phép tính tích phân.
• Dùng để mô tả dòng điện xoay chiều.

Dạng bài tập liên quan đến số phức

Sau đây là một số dạng bài tập cơ bản thường gặp liên quan đến số phức, các em hãy cùng theo dõi để có thể nắm vững được cách làm nha.

Dạng 1: Điểm biểu diễn của số phức bất kỳ

Đây là một dạng toán cơ bản nhất, để có thể hoàn thành tốt dạng bài tập này, các em cần nắm vững kiến thức sau:

Cho z = a + bi (a,b thuộc R), thì điểm biểu diễn M của z có tọa độ là (a,b) và ngược lại.

Ví dụ minh họa:

z = (3 + 5i ) + (-8 + 6i), tìm điểm biểu diễn z trên mặt phẳng tọa độ.

Lời giải:

Ta có : z = (3 + 5i ) + (-8 + 6i) = 3 - 8 + 5i + 6i = -6 + 11i, vậy điểm biểu diễn của z có tọa độ là M(-6, 11).

Dạng 2: Tìm số phức thỏa mãn điều kiện T cho trước

Để có thể làm tốt bài tập ở dạng này, các em chỉ cần dựa vào điều kiện đã cho ở để bài để giải phương trình tìm ra được phần thực và phần ảo, từ đó suy ra số phức cần tìm.

Ví dụ minh họa:

Cho đẳng thức: 5x + y + 5xi = 2y - 1 + (x - y)i, tìm x, y để đẳng thức đã cho là đúng.

Lời giải:

Ta coi 5x + y + 5xi và 2y - 1 + (x - y)i là số phức z. z’

z, z ‘ bằng nhau khi và chỉ khi:

5x + y = 2y - 1 và 5x = x - y

Suy ra: x = 1/7, y = 4/7.

Dạng 3: Tìm căn bậc hai của số phức

Cho số phức z = a + bi, w = x + yi được gọi là căn bậc hai của z, nếu w^2 = z.

• Nếu a > 0, có 2 căn bậc hai là a.
• Nếu a < 0, có 2 cặn bậc hai là |a|

Để giải dạng toán này, các em có thể áp dụng 1 trong 2 phương pháp sau nhé:

Phương pháp 1: Biển đổi z = a + bi dưới dạng bình phương của một số phức khác.

Phương pháp 2: Đẳ w = yi (x, y thuộc R) là một căn bậc hai của z, lúc này ta có:

w^2 = z khi và chỉ khi x^2 - y^2 = a và 2xy = b.

Ví dụ minh họa:

Cho z = 8 + 6i, tìm căn bậc 2 của z.

Lời giải:

Ta có, z = 8 + 6i = 9 + 6i - 1 = 3^2 +2.3i + i^2 = ( 3 + i)^2.

Vậy căn bậc 2 của z là (3 + i) và -(3 + i)

Dạng 4: Giải phương trình bậc 2 số phức

Đối với dạng toán này, các em chỉ cần nắm vững các bước sau là có thể dễ dàng tìm được đáp án rồi nè.

• Bước 1: Đặt = B2 - 4AC.
• Bước 2: Tìm căn bậc 2 của phương trình
• Bước 3: Tìm nghiệm của , với điều kiện:

Nếu = 0, phương trình có nghiệm kép z1 = z2 = -B/2A

Nếu khác 0, phương trình có 2 nghiệm lần lượt là z1 = (B + )/2A và z2 = -((B + )/2A, với là căn bậc 2 của .

Ví dụ minh họa: Cho phương trình z^2 + z + 1 =0, tìm tập nghiệm của pt này.

Lời giải:

Đặt = 1^2 - 4.1.1 = -3, = i3 và - i3.

Vì = -3 < 0, nên phương trình đã cho có 2 nghiệm là:

z1 = (-1 + i3)/2 và z2 = (-1 - i3)/2

Suy ra, pt đa cho có tập nghiệm là

S = {(-1 - i3)/2; (-1 + i3)/2}.

Dạng 5: Giải phương trình số phức bậc cao

Đây là một dạng bài tập nhìn thì có vẻ phức tạp nhất, tuy nhiên, các em chỉ cần bình tĩnh sử dụng các phép toán biến đổi như đặt ẩn phụ, phân tích thành nhân tử,... để hạ bậc phương trình bậc cao và tiến hành giải như bình thường thôi nè.

Ví dụ minh họa:

Giải phương trình z^4 + 1 = 0

Lời giải:

Ta có z^4 + 1 = 0 z^4 - i^2 = 0 (z^2 - i).(z^2 +i) = 0

z^2 = i và z^2 = -i.

• Với z^2 = i, ta có:

Gọi w = x + yi (x,y thuộc R) là căn bậc 2 của số phức z’ = i, lúc này:

w^2 = i x^2 - y^2 = 0 và 2xy = 1 x = y= 1/2; x = y = -1/2

z = 1/2 + (1/2)i và z = -1/2 - (1/2)i

• Với z^2 = -i, ta có:

z’ = -i = i^2.i nên ta có căn bậc 2 của z’ là:

i.(1/2 + (1/2)i) = -1/2 + (1/2)i và i.(-1/2 - (1/2)i) = 1/2 - (1/2)i

Vậy phương trình đã cho có 4 nghiệm là:

z1 = 1/2 + (1/2)i, z2 = -1/2 - (1/2)i, z3 = 1/2 - (1/2)i và z4 = -1/2 + (1/2)i .

Dạng 6: Tìm giá trị lớn nhất, nhỏ nhất của số phức

Đây là một dạng toán khá là thú vị, thường xuyên xuất hiện trong các bài kiểm tra quan trọng, muốn giải được dạng toán này, các em cần nắm vững các kiến thức sau:

|z1 + z2| |z1| + |z2|, dấu = xảy ra khi z1 = kz2, k lớn hơn hoặc bằng 0.

|z1 - z2| |z1| - |z2|, dấu = xảy ra khi z1 = kz2, k nhỏ hơn hoặc bằng 0.

|z1 + z2| ||z1| - |z2||, dấu = xảy ra khi z1 = kz2, k nhỏ hơn hoặc bằng 0.

|z1 - z2| ||z1| - |z2||, dấu = xảy ra khi z1 = kz2, k lớn hơn hoặc bằng 0.

• Để tìm min:

Áp dụng BĐT Cauchy: A^2 + B^2 (A + B)^2/2.

Áp dụng BĐT Mincopxki:

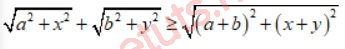
Dấu = xảy ra khi a/b = x/y.

Áp dụng BĐT vecto:

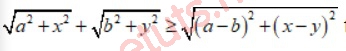
Dấu bằng xảy ra khi a/b = x/y

• Để tìm max, áp dụng BĐT Bunhia Copski: (Ax + By)^2 (A^2 + B^2)(x^2 + y^2).

Ví dụ minh họa:

Cho z, thỏa mãn |z + 1 - 5i| = |z + 3 -i|, tìm số phức có modun min.

Lời giải:

Đặt z = z + yi, (x, y thuộc R) , suy ra z = x - yi.

Theo đề bài, ta có:

|z + 1 - 5i| = |z + 3 -i| |x + yi + 1 - 5i| = |x - yi + 3 - i|

|(x + 1) + (y - 5)i| =|(x+3) + (-y -1)i|

(x + 1)^2 + (y - 5)^2 = (x + 3)^2 + (y + 1)^2

x^2 + 2x + 1 + y^2 - 10y + 25 = 0

x^2 + 6x + 9 + y^2 + 2y + 1 = 0

-4x - 12y + 16 = 0

x = 4 - 3y

Vậy, lúc này, ta có:

|z| = x2+y2=(4-3y)2 + y2=10y2 -24y + 16

= 10(y-6/5)2+8/5210/5

Dấu bằng xảy ra khi y = 6/5 , x = 2/5.

Vậy modun nhỏ nhất của |z| = 210/5, khi z = 2/5 + 6/5i.

Cách giải bài tập số phức bằng máy tính bỏ túi Casio

Có một cách nhanh chóng giúp các em có thể dễ dàng giải các bài tập liên quan đến số phức đó chính là sử dụng máy tính bỏ túi Casio, hãy làm theo hướng dẫn sau nha:

• Bước 1: Khởi động máy tính bỏ túi, bấm phím MODE + 2
• Bước 2: Đợi màn hình hiển thị dòng chữ CMPLX và tiến hành nhập phương trình vào như thông thường thôi nè.

Một số tính năng quan trọng mà các em cần lưu ý là:

• Phần ảo (i): Bấm phím ENG.
• Lấy modun: Bấm phím Shift + hyp.
• Số phức liên hợp (z): Bấm phím Shift + 2 + 2
• Argument: Bấm phím Shift + 2 + 1
• Phần thực: Bấm phím Shift + 2 + 3
• Phần ảo: Bấm phím Shift +2 + 4
• Đối sang dạng lượng giác: Bấm phím Shift + mũi tên xuống + 1
• Muốn đổi sang dạng đại số: Bấm phím Shift + mũi tên xuống + 2

Ví dụ minh họa: Tìm z , biết z = (3i - 2)/(i + 1).

Lời giải:

• Bước 1: Bấm MODE + 2, sau đó nhấn shift/2/2.
• Bước 2: Nhập phép tính (3i - 2)/(i + 1) vào máy tính, lúc này màn hình sẽ hiển thị Conjg(3i - 2)/(i + 1), và cho ra kết quả là 1/2 - 5/2i

Bài tập liên quan đến số phức

Sau khi đã nắm vững lý thuyết và các dạng bài tập cơ bản, bây giờ các em hãy vận dụng chúng để giải một số các bài tập dưới đây nha:

• Bài 1: Tìm số phức liên hợp của z = (3 - 2i).(2 + 3i)

Lời giải:

Ta có:

z = (3 - 2i).(2 + 3i) = 6 + 9i - 4i + 6 = 12 + 5i,

Vậy, số phức liên hợp của z là z = 12 - 5i

• Bài 2: Tìm modun của số phức z = 2 - 3i

Lời giải:

Ta có, modun của z = 2 - 3i là |z| = 22+(-3)2=13

• Bài 3: Tìm nghiệm z^3 - 8 = 0

Lời giải:

Ta có:

z^3 - 8 = 0 (z - 2)(z^2 + 2z + 4) = 0

z = 2 và z^2 + 2z + 4 = 0 z = 2 và (z + 1)^2 = -3

z = 2, z = -1 +3i, z = -1 - 3i.

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ tất tần tật các kiến thức liên quan đến số phức, hy vọng qua đây, các em sẽ củng cố lại được phần kiến thức quan trọng này để có thể thành thục giải các bài toán liên quan.