Công thức tính diện tích hình phẳng và bài tập vận dụng

Cách tính diện tích hình phẳng được giới hạn bởi 1 đường, 2 đường, 3 đường, đường tròn, đường parabol,...và các bài tập liên quan cùng cách giải chi tiết.

Tính diện tích hình phẳng là một trong những ứng dụng quan trọng của toán tích phân trong chương trình THPT, tuy nhiên, chắc hẳn còn nhiều học sinh vẫn cảm thấy bối rối trước nhiều dạng hình phẳng khác nhau. Chính vì thế, trong bài viết hôm nay, hãy cùng freetuts ôn tập lại các cách tính diện tích hình phẳng từ cơ bản đến nâng cao nha.

Cách tính diện tích hình phẳng cơ bản

Ngay bên dưới đây là cách tính S hình phẳng được giới hạn bởi 1 đường thằng và 2 đường thẳng, mời các em cùng xem qua nhé.

Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số và các trục

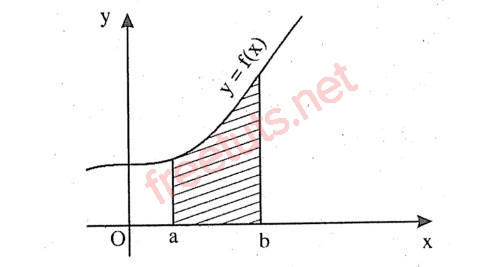
Hình phẳng giới hạn bởi đường f(x).

Cho hàm số y = f(x) liên tục trên [a,b], hình phẳng S được giới hạn bởi đồ thị hàm số y, trục hoành và hai đường thẳng x = a, x =b, lúc này diện tích hình S được tính bằng:

Bài viết này được đăng tại [free tuts .net]

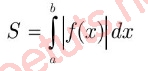
Ví dụ minh họa:

Hãy tính diện tích hình S được giới hạn bởi đồ thị hàm số y = x3-x, đường thẳng x = 2 và trục tung, trục hoành.

Lời giải:

Vì trục tung có phương trình tọa độ x = 0, ta có:

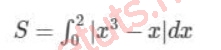
Vì: x3-x 0 0x1; x3-x 0 1x2,

Ta có:

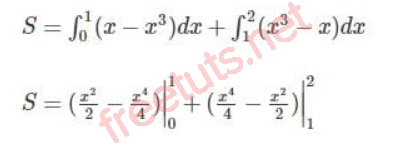
Vậy S = 1/4 + 9/4 = 5/2 (đvdt)

Tính diện tích hình phẳng được giới hạn bởi 2 đường

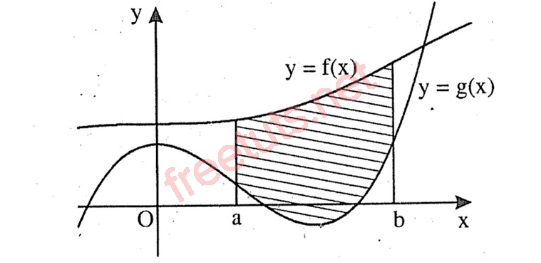
Hình phẳng giới hạn bởi hai đường y = f(x) và y = g(x).

Cho một hình phẳng bất kỳ, được giới hạn bởi hai đường y = f(x) và y = g(x), biết f(x), g(x) liên tục trên [a,b] và x = a, x = b

• Bước 1: Lập phương trình hoành độ giao điểm f(x) = g(x)
• Bước 2: Lúc này ta có công thức tính diện tích của hình phẳng là:

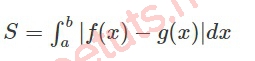
Ví dụ minh họa:

Cho hình phẳng M được giới hạn bởi hai đồ thị hàm số như sau, y = x2+2 và y = 3x, hãy tính diện tích M.

Lời giải:

Xác định hoành độ giao điểm bằng cách giải phương trình x2+2=3x

x2+2-3x=0x2-3x+2=0(x-1)(x-2)=0

x=1 và x= 2

Vậy hình phẳng M được giới hạn bởi đồ thị y = x2+2 và y = 3x và 2 đường thẳng x = 1 và x = 2.

Áp dụng ct tính S hình phẳng ở trên, ta có:

S=12|x2-3x+2|dx=12(x2-3x+2)dx=3x22-x33-2x)|12=16

Cách tính diện tích hình phẳng đặc biệt

Ngoài trường hợp các hình phẳng cơ bản trên, trong toán học các em sẽ thương xuyên gặp hình phẳng được cắt bởi nhiều đường, đồ thị hơn nữa. Hãy cùng freetuts điểm qua một số trường hợp đặc biệt dưới đây nha.

Tính diện tích hình phẳng giới hạn bởi 3 đường

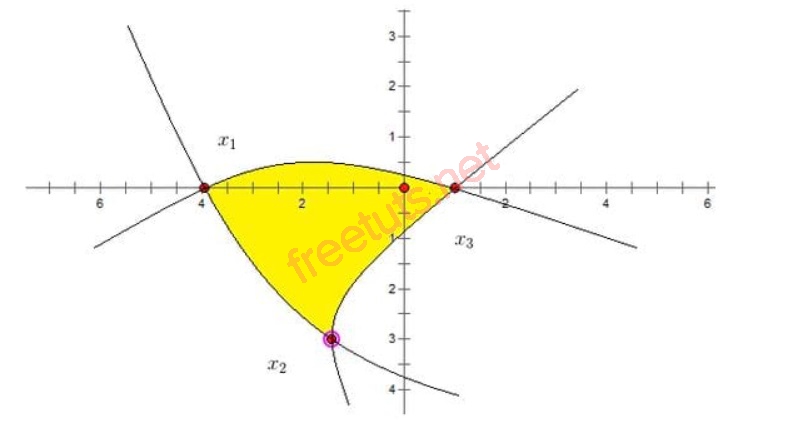
Hình phẳng S được giới hạn bởi 3 hàm số.

Cho hình phẳng S được giới hạn bởi 3 đồ thị hàm số y = f(x), y=g(x), y=h(x), để tính diện tích hình S, ta làm theo các bước sau:

• Bước 1: Tìm hoành độ giao điểm của các đồ thị hình S, x1; x2;x3 với x1x2x3
• Bước 2: Lúc này, diện tích hình S sẽ được tính theo công thức sau:

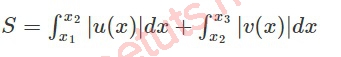
Với u(x) là hàm số của pt tìm x1, v(x) là hàm số của phương trình tìm x2

Ví dụ minh họa:

Cho hình phẳng S được giới hạn bởi 3 đường: y=3x, y=4-x, y=1, tính diện tích hình S.

Lời giải:

Ta tìm hoành độ giao điểm như sau:

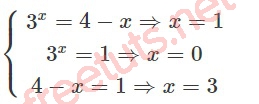
Áp dụng công thức tính diện tích hình phẳng S, ta có:

Tính diện tích hình phẳng giới hạn bởi parabol và 1 đường thẳng

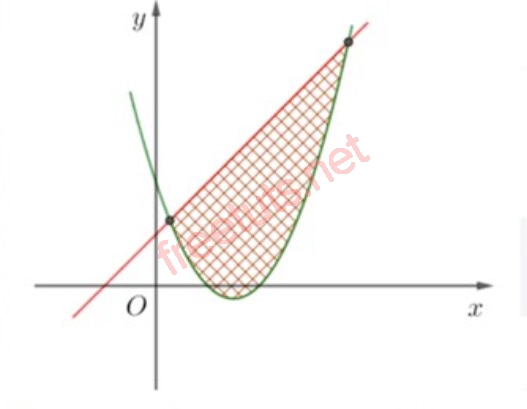
Hình phẳng giới hạn bởi (P) và đường thẳng bất kỳ.

Cho hình phẳng S được giới hạn bởi parabol (P) y = ax2+bx+c và đường thẳng y = mx +n.

• Bước 1: Xét phương trình hoành độ giao điểm, ta có:

ax2+bx+c= mx+n ax3+(b-m)x+c-n=0

• Bước 2: Lúc này, diện tích hình S được tính như sau:

S2=((b-m)2-4a(c-n))336a4

Ví dụ minh họa:

Cho parabol (P): y=x2, 2 điểm A, B thuộc P, AB = 63, Tính S hình phẳng được giới hạn bởi (P) và AB.

Lời giải:

Có, phương trình đi qua 2 điểm A, B là y=b2-a2b-a(x-a)+a2 = (a+b)x-ab.

Lúc này, ta có phương trình hoành độ giao điểm:

x2=(a+b)x-abx2-(a+b)x+ab=0.

Vậy, S hình phẳng được giới hạn bởi (P) và AB là:

S2=((a+b)2-4ab)336a4=(a-b)636.

Vì AB = 63 (a-b)2+(a2-b2)2=108 (a-b)2(1+(a+b)2)=108

(a-b)2=108(1+(a+b)2)108 S 108336 = 1083 (đvdt)

Tính diện tích hình phẳng giới hạn bởi parabol và một đường tròn

Đối với dạng toán này, các em cần làm theo hướng dẫn sau:

• Bước 1: Vẽ hình để xác định được hình phẳng cần tính diện tích,
• Bước 2: Sử dụng các công thức cơ bản ở trên để tính từng phần diện tích
• Bước 3: Cộng diện tích của các hình nhỏ lại để được diện tích hình cần tìm.

Ví dụ minh họa:

Tính diện tích hình S được giới hạn bởi parabol y = 2x và đường tròn có pt x2+y2=8

Lời giải:

Theo dữ liệu, ta có hoành độ giao điểm của P và đường tròn là nghiệm của hệ pt sau:

y = 2x ; x2+y2=8, với x 0

x2+2x -8 = 0 (x-2)(x+4)=0

x = 2 và x =-4

Với điều kiện x 0, nên chỉ có giá trị x = 2 là thỏa mãn.

Vậy, hoành độ giao điểm của đường tròn và trục hoành là x = 22 và x=-22

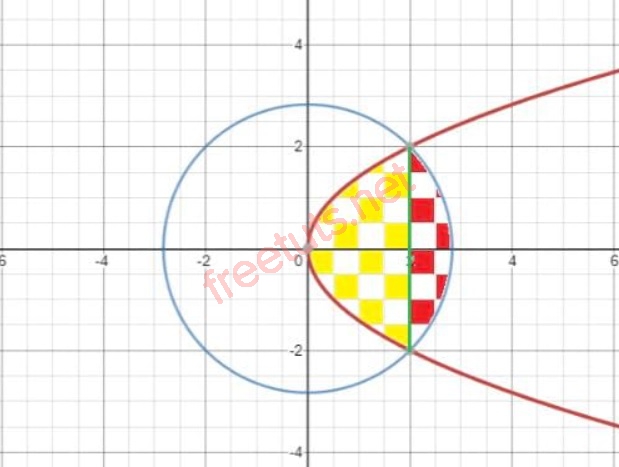
Dựa vào hình trên, ta có hình S được chia làm 2 phần gồm S1 là phần tô màu vàng và S2 là phần to màu đỏ.

S = S1 + S2

Với S1 là hình phẳng được giới hạn bởi parabol y = 2x và 2 đường thẳng x = 0, x= 2, ta có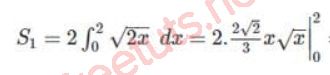

Vậy S1 = 8/3 (đvdt)

S2 là hình phẳng được giới hạn bởi đường tròn x2+y2 =8 và 2 đường x = 2, x= 22, diện tích hình S2 được tính bằng công thức:

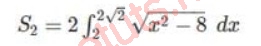
Đặt x = 22 sint với 0 t2

dx= 22cost dt

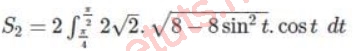
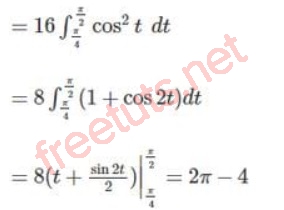
Vậy S = S1 + S2 = 2 + 4/3 (đvdt)

Tính diện tích hình phẳng giới hạn bởi đường cong bậc 3 và đường thẳng

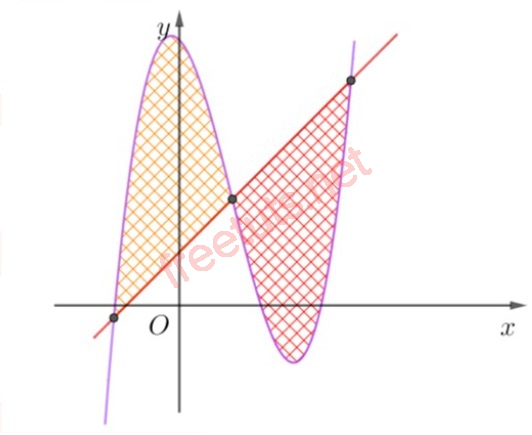
Hình phẳng giới hạn bởi đường cong bậc 3 và đường thẳng bất kỳ.

Cho đường thẳng y = mx + n cắt đường cong bậc 3: y = ax3+bx3+cx+dtại 3 điểm phân biệt. Lúc này, S hình phẳng giới hạn bởi hai đường này sẽ chia làm 2 phần bằng nhau điểm uốn I(-b3a; y(-b3a)) của đường cong bậc 3 thuộc y = mx + n

Bài tập tính diện tích hình phẳng

Sau khi đã nắm được các cách tính S hình phẳng ở trên, bây giờ, các em hãy áp dụng chúng để giải một số bài tập dưới đây nha:

Bài 1:

Cho hình phẳng T được giới hạn bởi đồ thị hàm số y = sin x + cos x - 2, trục hoành, trục tung và đường thẳng x = /2, bằng a + b, với a,b là số nguyên. Tính diện tích hình T.

Lời giải:

Ta có:

y = sinx + cosx - 2 < 0, x [0; /2].

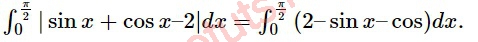
= (2x + cosx - sinx)|0/2 = -2

Với a = -2, b = 1 T = 2a + 3b = 2(-2)+3.1=-1

Vậy diện tích hình T = -1 (đvdt)

• Bài 2: Cho hình phẳng S được giới hạn bởi đồ thị hàm số y = x2+3x, trục tung Ox và hai đường thẳng x = 1, x =2.

Lời giải:

Xét phương trình:

x2+3x=0 x = 0 [1;2] và x =-3 [1;2].

Ta có, diện tích hình S được tính bằng công thức sau:

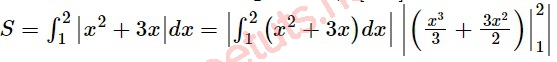
S = 41/6 (đvdt).

• Bài tập 3: Cho hình phẳng S được giới hạn bởi đường y = x2-x+3 và y = 2x + 1, tính diện tích hình S.

Lời giải:

Có phương trình hoành độ giao điểm của y = x2-x+3 và y = 2x + 1 là:

x2-x+3 = 2x + 1

x2-3x+2=0

x = 1 và x = 2

Lúc này, ta có

x2-3x+2 0 với mọi x thuộc [1;2], ta có:

S = 12|x2-3x+2|dx =-12|x2-3x+2|dx = 1/6 (đvdt).

Như vậy, qua bài viết trên, freetuts.net đã chia sẻ tất cả các công thức tính diện tích hình phẳng từ cơ bản đến nâng cao, hy vọng những thông tin này sẽ giúp các em nắm vững phần lý thuyết quan trọng này và có thể áp dụng vào giải các bài tập liên quan.