Thông báo: Download 4 khóa học Python từ cơ bản đến nâng cao tại đây.
Cách sử dụng hàm Broadcasting trong NumPy
Trong bài viết này, bạn sẽ tìm hiểu về kỹ thuật broadcasting trong NumPy và cách thức hoạt động của nó. Broadcasting là một kỹ thuật cho phép bạn thực hiện các phép toán số học trên các mảng có kích thước khác nhau một cách dễ dàng và hiệu quả. Việc nắm vững kỹ thuật này sẽ giúp bạn giải quyết nhiều bài toán xử lý dữ liệu và phân tích phức tạp hơn với NumPy. Hãy cùng tìm hiểu cách broadcasting hoạt động thông qua các ví dụ và quy tắc cơ bản của nó.

Giới thiệu về broadcasting trong NumPy
Trong các bài viết trước, bạn đã học cách thực hiện các phép toán số học trên các mảng có kích thước bằng nhau bằng cách sử dụng các hàm add(), subtract(), multiply(), và divide() hoặc các toán tử +, -, *, và /.
Để thực hiện các phép toán số học trên các mảng có kích thước khác nhau, NumPy sử dụng một kỹ thuật gọi là broadcasting.
Theo định nghĩa, broadcasting là một tập hợp các quy tắc để áp dụng các phép toán số học trên các mảng có kích thước khác nhau. Chúng ta sẽ đề cập chi tiết về các quy tắc này ngay sau đây.
Bài viết này được đăng tại [free tuts .net]
Trước tiên, hãy xem một số ví dụ đơn giản về broadcasting. Ví dụ, bạn có thể sử dụng toán tử + để cộng một số vào một mảng như sau:
import numpy as np a = np.array([1, 2, 3]) b = a + 1 print(b)
Kết quả:
[2 3 4]
Trong ví dụ này, ta cộng số 1 vào một mảng 1D sử dụng toán tử +. Nội bộ, NumPy cộng số 1 vào mỗi phần tử của mảng. Kỹ thuật này được gọi là broadcasting.
Nói cách khác, NumPy phát sóng số 1 qua chiều đầu tiên để khớp với hình dạng của mảng 1D.
Về mặt khái niệm, bạn có thể nghĩ về broadcasting trên như tương đương với:
import numpy as np a = np.array([1, 2, 3]) b = a + np.array([1, 1, 1]) print(b)
Vì vậy, việc cộng số 1 vào một mảng 1D giống như việc sao chép số 1 thành một mảng 1D khác [1, 1, 1] và cộng mảng đó vào mảng ban đầu:
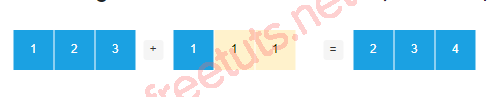
Tuy nhiên, NumPy thực hiện broadcasting số 1 mà không cần sao chép nó. Bằng cách làm này, NumPy có thể quản lý hiệu quả và tăng tốc độ tính toán trong hầu hết các trường hợp.
Tương tự, bạn có thể cộng một mảng 1D vào một mảng 2D bằng cách sử dụng broadcasting như sau:
import numpy as np
a = np.array([
[1, 2, 3],
[4, 5, 6]
])
b = np.array([10, 20, 30])
c = a + b
print(c)
Kết quả:
[[11 22 33] [14 25 36]]
Trong ví dụ này, NumPy phát sóng mảng 1D b qua chiều thứ hai để khớp với hình dạng của mảng a.
Quy tắc broadcasting của NumPy
NumPy định nghĩa một tập hợp các quy tắc cho broadcasting:
- Nếu hai mảng có số chiều khác nhau, NumPy sẽ thêm các chiều có kích thước là 1 vào phía bên trái của mảng có số chiều ít hơn.
- Nếu kích thước của hai mảng không khớp ở bất kỳ chiều nào, NumPy sẽ kéo dài (hoặc broadcast) mảng có kích thước là 1 ở chiều đó để khớp với kích thước của mảng kia.
- Nếu kích thước của bất kỳ chiều nào của hai mảng không bằng nhau và không bằng 1, NumPy sẽ gây ra lỗi.
Hãy xem một số ví dụ để hiểu rõ hơn các quy tắc này.
Broadcasting trên một mảng
Ví dụ sau đây cộng một mảng 2D với một mảng 1D:
import numpy as np
a = np.array([
[1, 2, 3],
[4, 5, 6]
])
b = np.ones(3)
c = a + b
print(c)
Kết quả:
[[2. 3. 4.] [5. 6. 7.]]
Bảng sau đây cho thấy kích thước của a và b:
| Mảng | Kích thước |
|---|---|
| a | (2, 3) |
| b | (3,) |
Theo quy tắc 1, vì mảng b có số chiều ít hơn, NumPy thêm một chiều với kích thước là 1 vào phía bên trái:
| Mảng | Kích thước |
|---|---|
| a | (2, 3) |
| b | (1, 3) |
Theo quy tắc 2, NumPy kéo dài chiều đầu tiên của mảng b để khớp với kích thước của mảng a:
| Mảng | Kích thước |
|---|---|
| a | (2, 3) |
| b | (2, 3) |
Bây giờ, kích thước của cả hai mảng đều khớp. Kích thước của mảng kết quả là (2, 3).
Broadcasting trên cả hai mảng
Ví dụ sau minh họa trường hợp NumPy broadcast cả hai mảng:
import numpy as np
a = np.array([
[1],
[2],
[3],
])
print(f"a shape: ", a.shape)
b = np.array([1, 2, 3])
print(f"b shape: ", b.shape)
c = a + b
print(c)
print(f"c shape: ", c.shape)
Kết quả:
a shape: (3, 1) b shape: (3,) [[2 3 4] [3 4 5] [4 5 6]] c shape: (3, 3)
Trong ví dụ này, kích thước của mảng a và b lần lượt là (3, 1) và (3,).
| Mảng | Kích thước |
|---|---|
| a | (3, 1) |
| b | (3,) |
Theo quy tắc 1, NumPy thêm một chiều với kích thước là 1 vào phía bên trái của mảng b:
| Mảng | Kích thước |
|---|---|
| a | (3, 1) |
| b | (1, 3) |
Theo quy tắc 2, NumPy kéo dài các chiều của cả hai mảng a và b để khớp:
| Mảng | Kích thước |
|---|---|
| a | (3, 3) |
| b | (3, 3) |
Mảng kết quả có kích thước là (3, 3).
Broadcasting với lỗi
Ví dụ sau đây cộng hai mảng không tương thích:
import numpy as np
a = np.array([
[1, 2],
[3, 4],
[5, 6],
])
print(f"a shape: ", a.shape)
b = np.array([1, 2, 3])
print(f"b shape: ", b.shape)
c = a + b
Nó sẽ gây ra lỗi:
a shape: (3, 2) b shape: (3,) ValueError: operands could not be broadcast together with shapes (3,2) (3,)
Trong ví dụ này, mảng a và b có kích thước lần lượt là:
| Mảng | Kích thước |
|---|---|
| a | (3, 2) |
| b | (3,) |
Theo quy tắc 1, NumPy thêm một chiều với kích thước là 1 vào phía bên trái của mảng b:
| Mảng | Kích thước |
|---|---|
| a | (3, 2) |
| b | (1, 3) |
Theo quy tắc 2, NumPy kéo dài chiều đầu tiên của mảng b từ 1 đến 3 để khớp:
| Mảng | Kích thước |
|---|---|
| a | (3, 2) |
| b | (3, 3) |
Theo quy tắc 3, vì các kích thước cuối cùng không khớp nhau và không bằng 1, NumPy sẽ gây ra lỗi.
Kết quả
Broadcasting trong NumPy là một tập hợp các quy tắc để áp dụng các phép toán số học trên các mảng có kích thước khác nhau. Hiểu và áp dụng đúng kỹ thuật này sẽ giúp bạn thực hiện các phép tính toán trên mảng một cách hiệu quả và linh hoạt. Bằng cách nắm vững kỹ thuật broadcasting, bạn có thể tối ưu hóa hiệu suất làm việc với dữ liệu và giải quyết các bài toán phức tạp một cách dễ dàng hơn. Hy vọng qua bài viết này, bạn đã có được cái nhìn tổng quan và ứng dụng được kỹ thuật này trong các dự án của mình.

 Các kiểu dữ liệu trong C ( int - float - double - char ...)
Các kiểu dữ liệu trong C ( int - float - double - char ...)  Thuật toán tìm ước chung lớn nhất trong C/C++
Thuật toán tìm ước chung lớn nhất trong C/C++  Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)  ComboBox - ListBox trong lập trình C# winforms
ComboBox - ListBox trong lập trình C# winforms  Random trong Python: Tạo số random ngẫu nhiên
Random trong Python: Tạo số random ngẫu nhiên  Lệnh cin và cout trong C++
Lệnh cin và cout trong C++  Cách khai báo biến trong PHP, các loại biến thường gặp
Cách khai báo biến trong PHP, các loại biến thường gặp  Download và cài đặt Vertrigo Server
Download và cài đặt Vertrigo Server  Thẻ li trong HTML
Thẻ li trong HTML  Thẻ article trong HTML5
Thẻ article trong HTML5  Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên  Cách dùng thẻ img trong HTML và các thuộc tính của img
Cách dùng thẻ img trong HTML và các thuộc tính của img  Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng 