Fancy Indexing trong NumPy

Trong các bài trước, chúng ta đã làm quen với một số phương thức để truy cập một phần của mảng như array slicing (vd: arr[:5]), masks (vd: arr[arr > 5]). Trong bài này, chúng ta sẽ tìm hiểu thêm về một cách thức truy cập khác được gọi là Fancy Indexing.

Nó cũng giống như các cách truy cập khác nhưng với tham số truyền vào là các mảng chỉ số, điều này sẽ khiến cho ta làm việc với các mảng dữ liệu lớn trở nên dễ dàng hơn.

1. Giới thiệu về Fancy Indexing

Cơ chế của Fancy Indexing nhìn chung khá đơn giản: chúng ta truyền vào một mảng chứa các vị trí của các phần tử cần lấy.

Ví dụ:

Bài viết này được đăng tại [free tuts .net]

import numpy as np
arr = np.random.randint(100, size=10)
print(arr)

[61 42 66 51 41  9 53 14 63 64]

Giả sử chúng ta muốn lấy 3 phần tử ở 3 vị trí khác nhau, thông thường thì ta sẽ làm thế này:

sub_arr = [arr[2], arr[5], arr[8]]
print(sub_arr)

[66, 9, 63]

Với Fancy Indexing, ta có thể truyền mảng chứa vị trí các phần tử (mảng chỉ mục) và nhận giá trị tương đương trên:

ind_arr = [2, 5, 8]
sub_arr = arr[ind_arr]
print(sub_arr)

[66  9 63]

Một điều quan trọng trong Fancy Indexing chính là mảng trả về sẽ có shape tương ứng với shape của mảng chỉ mục chứ không phải là mảng ban đầu:

index_arr = np.array([[1, 2],
                      [8, 9]])
sub_arr = arr[index_arr]
print(sub_arr)

[[42 66]
 [63 64]]

Fancy Indexing cũng hoạt động tương tự với mảng nhiều chiều:

arr = np.arange(16).reshape(4, 4)
print("arr = ", arr)

# Mảng row (hàng) và cột (col) chứa vị trí của các phần tử cần trích xuất
# Các phần tử gồm arr[0, 1], arr[1, 2] và arr[2, 3]
row = [0, 1, 2]
col = [1, 2, 3]

sub_arr = arr[row, col] 

print("sub_arr = ", sub_arr)

arr =  [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
sub_arr =  [ 1  6 11]

Trong Fancy Indexing, điều mà bạn luôn cần nhớ đó chính là mảng trả về sẽ luôn có shape tương ứng với shape của mảng chỉ mục chứ không phải là mảng ban đầu.

2. Combined Indexing (Chỉ mục kết hợp)

Fancy Indexing còn có một tính năng rất mạnh đó là nó có thể kết hợp với những kiểu truy cập mảng mà chúng ta đã học, khiến cho ta có thể thao tác nhiều phép toán phức tạp chỉ trong một dòng code. Chúng ta sẽ đến với từng trường hợp cụ thể

Fancy Indexing và chỉ mục đơn giản

Ta có thể kết hợp kiểu chỉ mục truyền thống mà ta thường dùng để lấy 1 phần tử và kết hợp với fancy indexing như sau:

arr = np.arange(16).reshape(4, 4)
print("arr = ", arr)

#Lấy các phần tử arr[3, 1], arr[3, 2] và arr[3, 3]
sub_arr = arr[3, [1, 2, 3]]
print("sub_arr = ", sub_arr)

arr =  [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]

sub_arr =  [13 14 15]

Fancy Indexing và Array Slicing

Ta có thể kết hợp giữa Fancy Indexing và Array Slicing (đã nói ở bài 2) như sau:

print("arr = ", arr)

# Lấy tất cả các phần tử nằm tại hàng >= 1 và các cột = 1, 2, 3 tương ứng
sub_arr = arr[1:, [1, 2, 3]]
print("sub_arr = ", sub_arr)

arr =  [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
sub_arr =  [[ 5  6  7]
 [ 9 10 11]
 [13 14 15]]

Hoặc phức tạp hơn với mảng 3 chiều:

arr = np.arange(18).reshape(3, 2, 3)
print("arr = ", arr)

print("sub_arr = ", arr[0, 1:, [0, 1]])

arr =  [[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]

 [[12 13 14]
  [15 16 17]]]

sub_arr =  [[3]
 [4]]

Fancy Indexing và Masks

Và cuối cùng, ta có thể kết hợp giữa Fancy Indexing và Masks:

arr = np.arange(16).reshape(4, 4)

print("arr = ", arr)

masks = arr[0, :] % 2 == 0
print("masks =", masks)

arr[:, masks]

arr =  [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
masks = [ True False  True False]

array([[ 0,  2],
       [ 4,  6],
       [ 8, 10],
       [12, 14]])

Ứng dụng Fancy Indexing trong chia tập dữ liệu

Chia tập dữ liệu là một trong những công việc khá phổ biến trong machine learning, trong đó chúng ta sẽ chia tập dữ liệu của chúng ta thành 2 phần: train và test nếu bạn chưa biết gì thì cũng đừng lo vì đây chỉ là một ví dụ của mình minh hoạ cho ứng dụng của Fancy Indexing. Giả sử mình sẽ tạo 1 tập dữ liệu mẫu và dùng matplotlib để biểu thị như sau:

import matplotlib.pyplot as plt
import seaborn; seaborn.set() # Thư viện chia cột đơn vị cho matplotlib

# Tạo mảng 2 chiều giá trị từ 1 -> 200
X = np.arange(200).reshape(100, 2)

# Thêm nhiễu cho mảng
noise = np.random.uniform(1, 30, X.shape)
X = X + noise

plt.scatter(X[:, 0], X[:, 1])

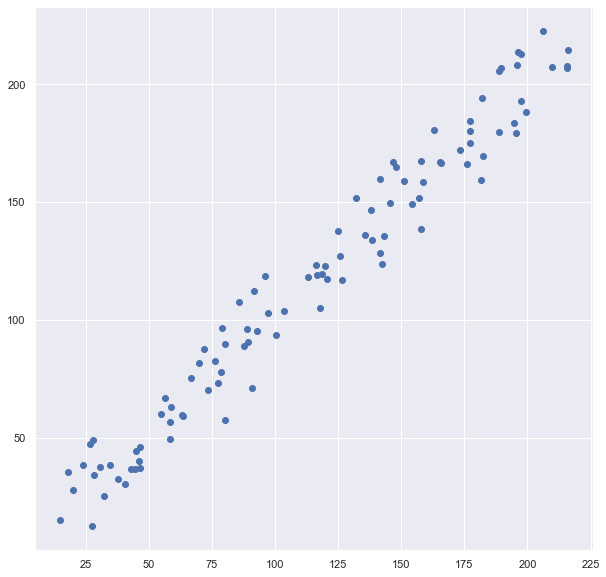
Bây giờ chúng ta sẽ lấy ngẫu nhiên các phần tử trong mảng với tỉ lệ là 80/20 (80% cho train, 20% cho test, với số lượng 200 phần tử thì ta sẽ lấy ngẫu nhiên 40 phần tử trong mảng X):

random_indices = np.random.choice(X.shape[0], 40, replace=False)
print("Vị trí các phần tử ngẫu nhiên: ", random_indices)
plt.figure(figsize=(10, 10))
# Fancy indexing
selection = X[random_indices]

# Hiển thị dữ liệu lên biểu đồ phân tán, với các phần tử bị làm mờ đi
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)

# Tô tròn các giá trị được chọn ngẫu nhiên bằng fancy indexing
plt.scatter(selection[:, 0], selection[:, 1], s=200, facecolors='none', edgecolors='r');

Vị trí các phần tử ngẫu nhiên:  [12  6 85 20 56 70 96 72 88 60 27 83 98 64  2 74 95 38 58 29 79 21 81 76
  7 94 57 52 23 91  4 66 68 50 87 84 39  3 78 16]

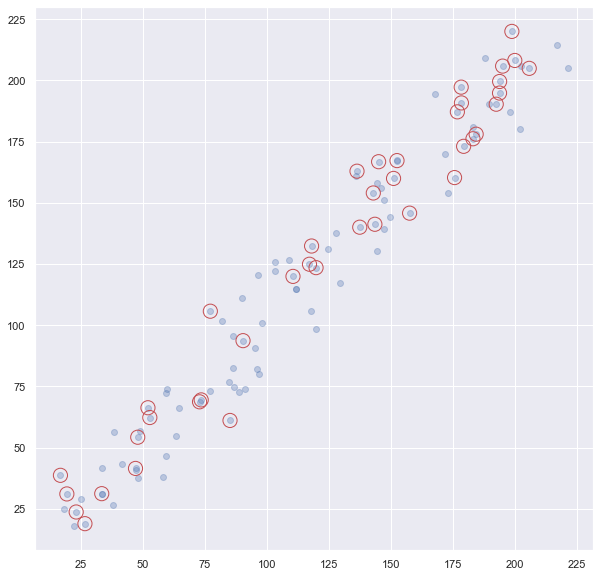
3. Thay đổi giá trị với Fancy Indexing

Tương tự với việc truy cập vào các mảng con, Fancy Indexing cũng có thể dùng để thay đổi giá trị tại các điểm, ví dụ:

x = np.array([1, 3, 5, 7, 9])
print("X = ", x)

i = np.array([0, 2, 4])
x[i] = 35

print("X = ", x)

X =  [1 3 5 7 9]
X =  [35  3 35  7 35]

Lưu ý là bạn cần quan tâm đến lựa chọn đúng shape của mảng chỉ mục, nếu lựa chọn sai sẽ dễ dẫn đến nhiều kết quả không mong muốn, chẳng hạn:

x = np.zeros(10)
print("x = ", x)
i = [[0, 0]]

x[i] = [2, 3]

print("x = ", x)

x =  [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
x =  [3. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

Chúng ta có thể thấy mảng x sau khi được thay đổi không chứa phần tử nào có giá trị bằng 2, lý do chính là vì mảng chỉ mục i. Khi thực hiện phép toán, đầu tiên nó sẽ được gán x[0] = 2, sau đó là x[0] = 3, vì vậy tất nhiên nó chỉ có phần tử = 3 mà thôi.

4. Tổng kết

Qua bài này ta đã tìm hiểu được về Fancy Indexing trong NumPy là gì và cách ứng dụng nó. Đây là một tính năng rất hữu ích giúp rút gọn code của bạn đi rất nhiều. Trong bài tới ta sẽ tìm hiểu về bài cuối cùng trong chương NumPy là Dữ liệu có cấu trúc trong NumPy nhé. Hẹn gặp các bạn ở bài tới.