Thông báo: Download 4 khóa học Python từ cơ bản đến nâng cao tại đây.
Tính toán trên mảng với NumPy
Tính toán trên mảng với NumPy có thể rất nhanh, nhưng đôi khi cũng rất chậm. Nhân tố chính khiến nó nhanh chính là nhờ vào các phép toán vectơ hoá (vectorized operations), được thêm vào trong Python qua các universal function (ufuncs). Trong bài này chúng ta sẽ cùng tìm hiểu về ufuncs, vectorized operations và các phép toán trên mảng với NumPy.

1. Các phép toán số học trong NumPy
Có 2 loại hàm toán học mà NumPy hỗ trợ, đó là unary functions (nhận một tham số duy nhất) và binary functions (nhận vào 2 tham số). Chúng ta sẽ đến với một số ví dụ cho cả hai loại hàm này:
Các hàm số học trên mảng
Một trong những ưu điểm tuyệt vời của NumPy đó là cho chúng ta cảm giác như đang thực hiện các phép toán bình thường với các biến trên Python,ví dụ như:
x = np.arange(5)
print("x =", x)
print("-x =", -x)
print("x + 2 =", x + 2)
print("x - 2 =", x - 2)
print("x * 2 =", x * 2)
print("x / 2 =", x / 2)
print("x // 2 =", x // 2) # Chia lấy phần nguyên
print("x ** 2 = ", x ** 2) # Luỹ thừa mũ 2
print("x % 2 = ", x % 2) # Chia lấy phần dưx = [0 1 2 3 4] -x = [ 0 -1 -2 -3 -4] x + 2 = [2 3 4 5 6] x - 2 = [-2 -1 0 1 2] x * 2 = [0 2 4 6 8] x / 2 = [0. 0.5 1. 1.5 2. ] x // 2 = [0 0 1 1 2] x ** 2 = [ 0 1 4 9 16] x % 2 = [0 1 0 1 0]
Hoặc bạn có thể viết như một biểu thức toán học:
Bài viết này được đăng tại [free tuts .net]
(-5*x + 3) / 2
array([ 1.5, -1. , -3.5, -6. , -8.5])
Ngoài việc dùng như một phép toán bình thường như trên, NumPy cũng cung cấp các hàm với tính năng tương tự, ví dụ như phép "+" tương ứng với hàm add:
print(x + 2) print(np.add(x, 2))
[2 3 4 5 6] [2 3 4 5 6]
Bạn có thể xem danh sách các hàm tương ứng với các phép toán số học ở bảng sau:
| Toán tử | Ufunc tương ứng | Chú thích |
| + | np.add | Phép cộng |
| - | np.subtract | Phép trừ |
| * | np.multiply | Phép nhân |
| / | np.divide | Phép chia |
| // | np.floor_divide | Phép chia lấy phần nguyên |
| ** | np.power | Phép luỹ thừa |
| % | np.mod | Phép chia lấy phần dư |
| - | np.negative | Phép lấy ngược dấu |
Giá trị tuyệt đối (absolute value)
Cũng giống như việc NumPy có thể dùng các phép toán cộng, trừ,... của Python, thì NumPy cũng có thể hiểu được hàm lấy giá trị tuyệt đối mặc định của Python:
y = np.array([-5, -4, -3, 3, 2, 1]) abs(y)
array([5, 4, 3, 3, 2, 1])
Ufunc tương ứng của NumPy là hàm np.absolute hoặc np.abs (cả 2 đều giống nhau):
print(np.absolute(y)) print(np.abs(y))
[5 4 3 3 2 1] [5 4 3 3 2 1]
Một điểm đáng quan tâm của ufunc này đó là nó có thể xử lý được số phức, nó sẽ trả về module của số phức tương ứng trong mảng, ví dụ:
z = np.array([1 - 2j, 0 + 1j, 3 + 4j]) np.abs(z)
array([2.23606798, 1. , 5. ])
Công thức tính module của số phức được tính như sau:
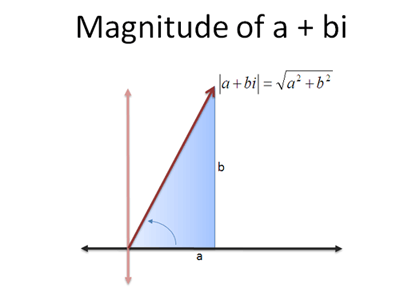
Hàm lượng giác
NumPy cung cấp một số các ufunc liên quan đến hàm lượng giác, đầu tiên hãy nhớ lại là hồi cấp 3 chúng ta đã từng học về vòng tròn lượng giác như sau:
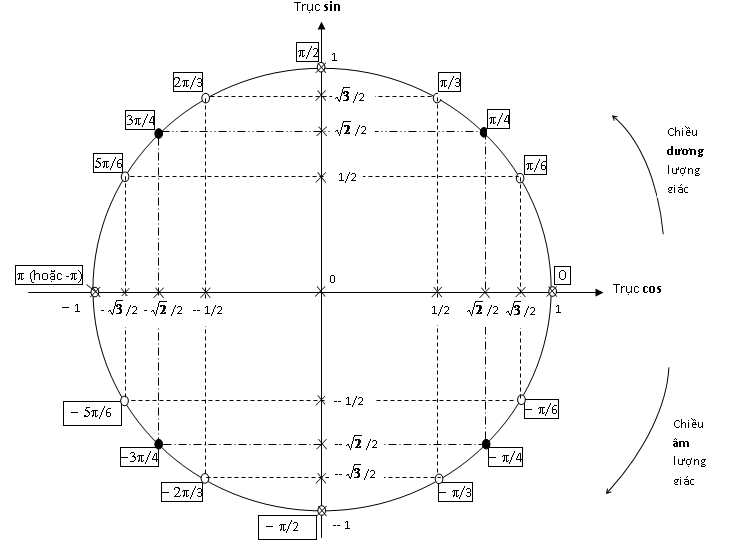
Chúng ta sẽ tạo một mảng chứa các giá trị sau:
theta = np.array([0, np.pi / 2, np.pi, 3*np.pi/2, np.pi * 2]) # Mảng có giá trị lần lượt là 0, pi/2, pi, 3pi/2 và 2pi print(np.sin(theta)) print(np.cos(theta))
[ 0.0000000e+00 1.0000000e+00 1.2246468e-16 -1.0000000e+00 -2.4492936e-16] [ 1.0000000e+00 6.1232340e-17 -1.0000000e+00 -1.8369702e-16 1.0000000e+00]
Các giá trị không thể bằng 0 tuyệt đối do hệ thống dấu phẩy động của máy tính (các bạn có thể đọc thêm), còn lại thì ta có thể thấy là các giá trị trên đều khớp với vòng tròn lượng giác đã nêu.
Ngoài ra các hàm lượng giác đảo cũng đều được hỗ trợ:
x = [-1, 0, 1] print(np.arcsin(x)) print(np.arccos(x)) print(np.arctan(x))
[-1.57079633 0. 1.57079633] [3.14159265 1.57079633 0. ] [-0.78539816 0. 0.78539816]
Hàm luỹ thừa và logarit
Hàm luỹ thừa trong NumPy có cú pháp như sau:
x = [1, 2, 3, 4]
print("x = ", x)
print("e^x =", np.exp(x))
print("2^x =", np.exp2(x))
print("3^x =", np.power(3, x))x = [1, 2, 3, 4] e^x = [ 2.71828183 7.3890561 20.08553692 54.59815003] 2^x = [ 2. 4. 8. 16.] 3^x = [ 3 9 27 81]
Ngược lại với luỹ thừa, ta có các hàm logarit:
print("x =", x)
print("ln(x) =", np.log(x))
print("log2(x) =", np.log2(x))
print("log10(x) =", np.log10(x))x = [1, 2, 3, 4] ln(x) = [0. 0.69314718 1.09861229 1.38629436] log2(x) = [0. 1. 1.5849625 2. ] log10(x) = [0. 0.30103 0.47712125 0.60205999]
NumPy cũng cung cấp một số hàm đặc biệt với tham số là các giá trị rất nhỏ, các hàm này sẽ xuất ra số thập phân chi tiết hơn so với những hàm bên trên:
x = [0, 0.0001, 0.001, 0.01, 0.1]
print("exp(x) - 1 =", np.expm1(x))
print("log(1 + x) =", np.log1p(x))exp(x) - 1 = [0.00000000e+00 1.00005000e-04 1.00050017e-03 1.00501671e-02 1.05170918e-01] log(1 + x) = [0.00000000e+00 9.99950003e-05 9.99500333e-04 9.95033085e-03 9.53101798e-02]
Nhìn chung ta có thể thấy các hàm số học trong NumPy được hỗ trợ rất nhiều cũng như rất tiện dụng. Một đặc điểm khác khiến NumPy phổ biến chính là vì nó rất nhanh, và chìa khoá cho việc đó chính là vectorized operation (vectơ hoá). Trong phần tiếp theo ta sẽ tìm hiểu cụ thể về vectorized operation.
2. Vectorized operations là gì? Ưu điểm của vectorized operation
Trong bài 2, chúng ta đã nói về việc một mảng trong NumPy phải là mảng đồng nhất về dữ liệu, ví dụ như một mảng có thể gồm một số nguyên (integer) hoặc số thực (float), nhưng không thể chứa cả hai được. Điều này đem đến một lợi thế lớn đó là vì NumPy "biết" được kiểu dữ liệu, nó có thể ủy quyền nhiệm vụ thực hiện các phép toán trên nội dung của mảng cho C biên dịch và tối ưu hóa, đây chính là vectorized operation. Kết quả chính là tốc độ của phép toán được tăng lên đáng kể so với việc xử lý phép toán tương tự trên Python.
Ta sẽ đến một ví dụ đó là tính tổng các số nguyên từ 0 => 99999 với NumPy và vòng lặp for trong Python để kiểm tra:
#Freetuts.net
#Khai báo mảng x với số phần tử từ 0 => 9999 và hàm sum để tính tổng theo vòng lặp for
x = np.arange(10000)
def sum(x):
total = 0
for i in x:
total = i + total
return totalTa sẽ sử dụng một magic function hỗ trợ trong IPython là %timeit để đo thời gian thực hiện:
%timeit np.sum(x) #Đo thời gian thực thi của NumPy %timeit sum(x) #Đo thời gian thực thi của vòng for
16.1 µs ± 2.44 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each) 4.16 ms ± 174 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Như vậy ta có thể thấy rõ sự khác biệt: sử dụng ufunc np.sum với việc đã được vectorized cho tốc độ nhanh hơn khoảng 258 lần (16.1 µs vs 4.16 ms) so với việc sử dụng Python thuần tuý. Tất cả các ufunc được hỗ trợ bởi NumPy đều được vectorized, do đó khuyến khích bạn nên sử dụng chúng thay vì thực hiện bằng Python.
3. Tính toán trên các mảng khác chiều với broadcasting
Qua phần trên, ta đã thấy sử dụng ufunc trong NumPy loại bỏ đi sự chậm chạp của Python một cách rất hiệu quả. Bên cạnh đó, NumPy còn cung cấp một tính năng rất hữu ích là broadcasting. Broadcasting là một tập hợp các quy tắc áp dụng cho binary ufuncs (cộng, trừ, nhân, chia,... đã nói ở trên) trên các mảng khác kích thước.
Giới thiệu về broadcasting
Quay lại với một ví dụ đơn giản về cộng 2 mảng cùng kích thước như sau:
a = np.array([0, 1, 2]) b = np.array([3, 3, 3]) a + b
array([3, 4, 5])
Broadcasting cho phép các tính toán này có thể thực hiện trên các mảng với số chiều khác nhau, chẳng hạn đối với ví dụ trên, ta có thể đơn giản hoá bằng cách cộng một số vô hướng (có số chiều bằng 0):
a + 3
array([3, 4, 5])
Chúng ta có thể tưởng tượng đơn giản là số 3 trên đã kéo dài ra thành một mảng [3, 3, 3] giống như ở ví dụ 1.
Ta có thể làm như thế với các mảng với số chiều cao hơn, chẳng hạn như mảng 2 chiều với mảng một chiều:
m = np.ones((3, 3))
print(m)
print("m + a =")
print(m + a)[[1. 1. 1.] [1. 1. 1.] [1. 1. 1.]] m + a = [[1. 2. 3.] [1. 2. 3.] [1. 2. 3.]]
Ở đây mảng a đã giãn ra thành mảng 2 chiều để khớp với mảng m và thực hiện phép toán giống như mảng 1 chiều cộng với một số vô hướng vậy.
Trên là các ví dụ cơ bản, giờ ta sẽ đến một ví dụ nâng cao sau đây:
a = np.arange(3)
b = np.arange(3)[:, np.newaxis]
print(a)
print(b)
print("a + b = ", a + b)[0 1 2] [[0] [1] [2]] a + b = [[0 1 2] [1 2 3] [2 3 4]]
Có thể bạn sẽ hơi khó hiểu về ví dụ này. Ở đây, chúng ta không còn giãn 1 mảng để khớp với mảng kia nữa mà cả 2 mảng cùng giãn để khớp với nhau. Ta có thể xem hình dưới để có thể hình dung về ví dụ này:
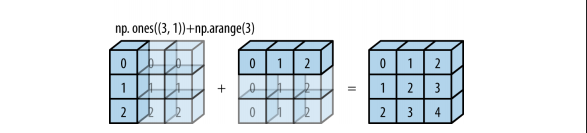
Các hộp in đậm là giá trị thực, còn các hộp nhạt màu là các giá trị được thêm vào để 2 mảng khớp với nhau.
Nếu như bạn đã hiểu cơ chế của broadcasting, thì đây thực sự là một công cụ vô cùng hữu ích khi thao tác với mảng, giúp ta giảm code đi rất nhiều.
Các quy tắc của broadcasting
Broadcasting có thể thực hiện được nếu như thoả mãn các quy tắc sau (các thuộc tính ndim, shape,... đã nói ở bài 2):
- Nếu 2 mảng khác kích thước, mảng có ndim nhỏ hơn mảng kia được thêm '1' vào (bên trái) shape của mảng đó.
- Nếu shape của 2 mảng không tương ứng ở bất cứ chiều nào, mảng có shape bằng 1 tại chiều nào thì chiều đó sẽ giãn ra để tương ứng với shape kia.
- Nếu trong bất kỳ kích thước nào mà kích thước không bằng nhau và không bằng 1, thì sẽ báo lỗi.
3 quy tắc trên đọc nhìn chung khá khó hiểu, mình sẽ đi vào từng ví dụ cụ thể:
Ví dụ 1: Cộng mảng 2 chiều với mảng 1 chiều
M = np.ones((2, 3)) a = np.arange(3)
Ở đây ta có shape của 2 mảng là:
M.shape = (2, 3) a.shape = (3,)
Theo quy tắc 1, ta sẽ thêm một vào phía bên trái shape của mảng a:
M.shape -> (2, 3) a.shape -> (1, 3)
Theo quy tắc 2, thì chiều có giá trị = 1 sẽ giãn ra để tương ứng với shape còn lại:
M.shape -> (2, 3) a.shape -> (2, 3)
Và ta thấy 2 shape đều chung kích thước (2, 3). Vậy output sẽ là:
M + a
array([[1., 2., 3.],
[1., 2., 3.]])Ví dụ 2: Cả 2 mảng đều broadcast
Xét 2 mảng:
a = np.arange(3).reshape((3, 1)) b = np.arange(3)
Đầu tiên, ta xét shape của 2 mảng:
a.shape = (3, 1) b.shape = (3,)
Theo quy tắc 1:
a.shape -> (3, 1) b.shape -> (1, 3)
Theo quy tắc 2:
a.shape -> (3, 3) b.shape -> (3, 3)
Vì cả 2 shape đã tương đương nhau, ta có kết quả:
a + b
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])Ví dụ 3: Cả 2 mảng không thể broadcast
Ta xét 2 mảng:
M = np.ones((3, 2)) a = np.arange(3)
Shape của 2 mảng:
M.shape = (3, 2) a.shape = (3,)
Theo quy tắc 1:
M.shape -> (3, 2) a.shape -> (1, 3)
Theoq quy tắc 2:
M.shape -> (3, 2) a.shape -> (3, 3)
Và như ta thấy, quy tắc 3 đã bị vi phạm do shape của 2 mảng sau khi đã giãn ra không trùng khớp, nếu như ta thử cộng 2 mảng này thì sẽ nhận lỗi sau:
M + a
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-24-8cac1d547906> in <module> ----> 1 M + a ValueError: operands could not be broadcast together with shapes (3,2) (3,)
4. Một số tính năng nâng cao trong tính toán với NumPy
Chỉ định đầu ra (Specifying output)
Nếu như đang tính toán với các mảng lớn, ta có thể chỉ định một mảng để lưu dữ liệu thay vì tạo một mảng mới, ví dụ:
a = np.arange(10) b = np.empty(10) np.multiply(a, 10, out=b) print(b)
[ 0. 10. 20. 30. 40. 50. 60. 70. 80. 90.]
Hoặc chi tiết hơn, ta có thể chỉ định lưu trữ tại từng phần tử của mảng:
a = np.arange(5) b = np.zeros(10) np.power(2, a, out=b[::2]) print(b)
[ 1. 0. 2. 0. 4. 0. 8. 0. 16. 0.]
Tổng hợp (Aggregates)
Trong một số trường hợp ta cần tổng hợp tất cả các giá trị của mảng bằng một phép toán trực tiếp trên các ufunc, NumPy cho ta một phương thức hữu ích là reduce.
Ví dụ như nếu ta thêm reduce sau hàm add, nó sẽ tính tổng tất cả các giá trị trong mảng:
x = np.array([0, 1, 2, 3]) np.add.reduce(x)
6
Tương tự, nếu sau hàm multiply, nó sẽ nhân tất cả các giá trị trong mảng:
np.multiply.reduce(x)
0
Và reduce cũng được áp dụng tương tự với các ufunc khác.
Outer products
Phương thức outer cho phép áp dụng ufunc cho tất cả các phần tử trong 2 mảng đầu vào, ví dụ:
np.multiply.outer([1, 2, 3], [4, 5, 6])
array([[ 4, 5, 6],
[ 8, 10, 12],
[12, 15, 18]])Biểu diễn bằng mặt toán học thì với hàm np.op.outer(A, B) (op là ufunc của NumPy, chẳng hạn add, multiply,...), cho M = A.dim, N = B.dim thì ta sẽ có output là C thoả mãn công thức:
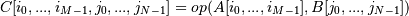
Với A, B là mảng một chiều thì nó tương ứng với đoạn code sau:
r = empty(len(A),len(B))
for i in range(len(A)):
for j in range(len(B)):
r[i,j] = op(A[i], B[j]) # op = ufunc 5. Tổng kết
Đây là một bài khá dài và bao quát gần như các thao tác tính toán trong NumPy, với mỗi phần trong bài bạn nên làm lại với nhiều ví dụ khác nhau (mà bạn tự nghĩ ra), như thế sẽ dễ để tiếp thu hơn. Trong bài tiếp theo ta sẽ tìm hiểu các hàm của NumPy ứng dụng trong xác suất và thống kê, hẹn gặp bạn ở bài tiếp theo.

 Các kiểu dữ liệu trong C ( int - float - double - char ...)
Các kiểu dữ liệu trong C ( int - float - double - char ...)  Thuật toán tìm ước chung lớn nhất trong C/C++
Thuật toán tìm ước chung lớn nhất trong C/C++  Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)  ComboBox - ListBox trong lập trình C# winforms
ComboBox - ListBox trong lập trình C# winforms  Random trong Python: Tạo số random ngẫu nhiên
Random trong Python: Tạo số random ngẫu nhiên  Lệnh cin và cout trong C++
Lệnh cin và cout trong C++  Cách khai báo biến trong PHP, các loại biến thường gặp
Cách khai báo biến trong PHP, các loại biến thường gặp  Download và cài đặt Vertrigo Server
Download và cài đặt Vertrigo Server  Thẻ li trong HTML
Thẻ li trong HTML  Thẻ article trong HTML5
Thẻ article trong HTML5  Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên  Cách dùng thẻ img trong HTML và các thuộc tính của img
Cách dùng thẻ img trong HTML và các thuộc tính của img  Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng 