Bài 12: Giải thuật đệ quy trong php

Đệ quy là một vấn đề nan giải đối với những bạn mới học lập trình web vì nó được sử dụng trong các ứng dụng như đệ quy menu đa cấp, chuyên mục đa cấp nhưng thực sự người nắm được giải thuật này không nhiều, vì thế trong loạt series php căn bản này ta sẽ tìm hiểu thêm về giải thuật này nhé.

Nội dung bao gồm:

• Đệ quy là gì?
• Đệ quy tuyến tính
• Đệ quy nhị phân
• Đệ quy hổ tương
• Khử đệ quy

1. Giải thuật đệ quy là gì ?

Đệ quy liên quan đến rất nhiều trong toán học, vì thế ta quay lại toán học một chút, một tính chất trong toán học được gọi là đệ quy nếu trong đó một lớp các đối tượng có các tính chất giống nhau và có mối liên hệ với nhau, kết quả của bước 1 là một thành phần của bước 2, bước 2 là thành phần bước 3, ….

Ví dụ: Ba của tôi là ông A, Ba của Ba tôi là ông B, … cứ như vậy đệ quy n lần sẽ tìm được nguồn gốc của tôi ( hơi căng ), và đây có thể gọi là một chương trình đệ quy nhằm tìm ra nguồn gốc của tôi. Giải thuật đệ quy cũng có thể gọi là phương pháp chia để trị (chia nhỏ từng phần ra rồi kết hợp lại sẽ dễ dàng hơn).

Bài viết này được đăng tại [free tuts .net]

Muốn dùng được đệ quy bạn phải biết viết hàm vì mỗi lần đệ quy là hàm gọi lại chính nó. Một chương trình đệ quy phải có điều kiện dừng, vì nếu không có thì chương trình sẽ gọi vô hạn (lặp vô hạn). Ví dụ tính tổng từ 1 tới n thì điều kiện dừng là khi tới n rồi thì không được tính nữa. còn nếu tính từ n trở về 1 thì điều kiện dừng là n = 1.

2. Đệ quy tuyến tính

Đây là loại đệ quy mà trong hàm đệ quy chỉ gọi duy nhất 1 lần đến chính nó.

Ví dụ: Cho n = 100, tính tổng các số từ 1 tới 100.

Bài này nếu dùng vòng lặp thì đơn giản, ta lặp từ 1 đến 100 và mỗi vòng lặp cộng dồn lại sẽ ra tổng. Bài giải cho vòng lặp như sau:

function tinhtong($n){
    $tong = 0;
    for ($i = 1; $i <= $n; $i++){
        $tong += $i; // mỗi vòng lặp cộng lại với nhau
    }
    return $tong;
}

Còn với giải thuật đệ quy thì ý tưởng là ở mỗi lần đệ quy ta sẽ lấy số đó cộng với hàm chính nó và biến truyền vào là số đó trừ đi 1. Điều kiện dừng là nếu số đó = 1 thì dừng vòng lặp và trả kết quả về. Phân tích kỹ hơn tức là mỗi bước đệ quy chính là một lần lặp, cộng dồn tổng các lần đệ quy chính là cộng dồn tổng các lần lặp nên kết quả nó sẽ thương đương với bài giải bằng vòng lặp trên.

function tinhtong($n)
{
    if ($n == 1){ return $n; }
    return $n + tinhtong($n-1);
}
echo tinhtong(100);

Trong giải thuật đệ quy này thì trong  hàm gọi lại chính nó chỉ 1 lần (tức là chỉ có 1 đoạn code tinhtong($n-1)). Ở mỗi bước đệ quy sẽ lấy giá trị $n truyền vào cộng với giá trị của tinhtong($n-1), cứ lặp đệ quy như vậy cho tới khi biến $n truyền vào hàm = 1 thì dừng đệ quy, bài toán được mô phỏng như sau:

Biến $n truyền vào = 100; giá trị return = 100 + đệ quy lần 2 với tham số như sau: tinhtong(100-1). Cứ như vậy mỗi lần đệ quy quy sẽ bằng biến truyền vào + lần đệ quy tiếp.

Luồng cộng như sau: 100 + ( 100-1 = 99 ) + (99 – 1 = 98) + …. + (2-1 = 1)  <=> 100 + 99 + 98 + …. + 1

3. Đệ quy nhị phân

Đệ quy nhị phân là loại đệ quy mà thân hạm gọi lại chính nó 2 lần.

Ví dụ: Xuất ra màn hình phần tử thứ 100 của dãy Fibonacci.

Dãy Fibonacci là dãy bắt đầu từ 1 tới n trong đó phần tử thứ $i trong dãy sẽ bằng tổng 2 phần tử trước nó cộng lại.  Ví dụ viết dãy từ Fibonacci của 8 phần tử đầu tiên thì ta viết như sau: 1 – 1 – 2 – 3 – 5  – 8  – 13 – 21.

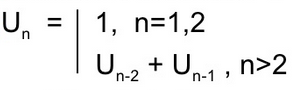
Trong dãy Fibonacci phần tử thứ 1 và thứ 2 có giá trị bằng 1. Đây cũng chính là điêu kiện dừng của dãy.

Bài giải:

// Hàm tính giá trị của phần tử thứ $n của dãy Fibonacci
function Fibo($n)
{
    if ($n <= 2){
        return 1;
    }
    else {
        return (Fibo($n - 2) + Fibo($n - 1));
    }
}
 
// Truyền 100 vào để test
echo Fibo(100);

3. Đệ quy phi tuyến

Là loại đệ quy mà trong hàm có dùng vòng lặp để gọi lại chính nó.

Ví dụ: Tính phần tử thứ 8 của dãy được tính theo công thức sau:

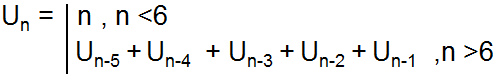
Ý nghĩa của dãy như sau:

• Nếu n nhập vào mà bé hơn 6 thì trả về chính nó
• Nếu n nhập vào mà lớn hơn hoặc bằng 6 thì trả về kết quả bằng tổng các số từ 1 tới n-1, với mỗi số lại tính theo quy luật trên. Có nghĩa rằng ví dụ tôi có hàm  phep_tinh và nhập giá trị 6 vào thì dãy được tính như sau: pheptinh(5) + pheptinh(4) + pheptinh(3) + pheptinh(2) + pheptinh(1)

Bài giải:

function pheptinh($n)
{
    // Neeus $n < 6 thì trả về chính nó
    if ($n < 6){
        return $n;
    }
    else{
        // Ngược lại tính tổng từ 1 tới $n - 1, và mỗi phần tử lại gọi làm hàm chính nó
        $tong = 0;
        for ($i = 1; $i < $n; $i++){
            $tong += pheptinh($n - $i);
        }
        return $tong;
    }
}
 
echo pheptinh(6);

4. Đệ quy hổ tương

Nghe cái tên thôi cũng hiểu được phần nào. Đệ quy hổ tương là đệ quy một hàm A gọi sang một hàm B, Trong hàm B lại gọi sang hàm A. Như vậy là chúng gọi lẫn nhau nên người ta gọi là  hổ tương.

Cũng như các loại đệ quy trên kia, nếu cả 2 hàm A, B đều không có điều kiện dừng thì sẽ bị lặp vô hạn, điều này rất nguy hiểm nên các bạn phải chú ý.

Ví dụ: Tính giá trị của dãy sau

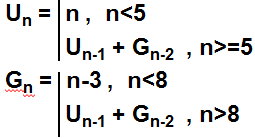
Ta thấy 2 hàm đệ quy có gọi lẫn nhau và mỗi hàm đều có điều kiện dừng. Đến đây hy vọng tôi không cần giải thích ý nghĩa của 2 hàm này nữa. Dựa vào cấu trúc của 2 hàm này tôi có bài giải như sau:

// Hàm đệ quy U
function U($n)
{
    if ($n < 5){ // điều kiện dừng
        return $n;
    }
    else{
        return U($n - 1) + G($n - 2);
    }
}
 
// Hàm đệ quy G
function G($n)
{
    if ($n <= 8){ // điều kiện dừng
        return $n - 3;
    }
    else{
        return U($n - 1) + G($n - 2);
    }
}
 
// Gọi Hàm
 
echo G(12);

5. Khử đệ quy

Giải thuật đệ quy rất hay nhưng chi phí tính toán cho nó thì rất mà cao, vì thế người ta hay tìm những giải thuật khác để thay thế cho nó. Tuy  nhiên trên thực tế chưa có một giải thuật nào chắc chắn cho điều này, có nghĩa là không phải bài nào cũng chuyển được. Và phần này là một quá trình nên tôi không có thời gian và cũng như là không đủ trình độ để giải hết các bài đệ quy được. Như ví dụ ở phần đệ quy tuyến tính các bạn thấy tôi đã dùng vòng lặp for để giải cho bài toán tính tổng. đó cũng là một cách dùng vòng lặp để khử đệ quy.

6. Lời kết

Giải thuật đệ quy thật sự rất khó phải không các bạn, nên để nắm được nó cần phải luyện tập nhiều thời gian. Tôi hy vọng qua bài này sẽ làm tiền đề cho các bạn đam mê giải thuật tìm tòi thêm. Bài tiếp theo chúng ta sẽ tìm hiểu một thuật toán khác liên quan đến sắp xếp, đó là thuật toán sắp xếp nổi bọt.