Mảng hai chiều trong Java
Trong bài trước, các bạn đã được tìm hiểu về mảng một chiều trong Java. Sang bài này, tôi sẽ giới thiệu đến các bạn một khái niệm mảng mới phức tạp hơn mảng một chiều, đó là khái niệm mảng hai chiều trong Java. Sau khi đã nắm được phần lý thuyết tôi đã trình bày trong bài này thì tôi sẽ đưa ra một số bài tập để các bạn luyện tập.

1. Mảng hai chiều trong Java
Như đã nói trong bài trước, mảng hai chiều là mảng có 2 chỉ số để lưu trữ các giá trị (chẳng hạn giá trị của một bảng có m dòng, n cột). Sau đây chúng ta sẽ đi tìm hiểu chi tiết về nội dung của bài học này.
Cú pháp khai báo mảng
Tương tự như khai báo mảng 1 chiều, cú pháp khai báo mảng 2 chiều có 2 dạng như sau:
Dạng 1:
Bài viết này được đăng tại [free tuts .net]
[Kiểu_dữ_liệu] Tên_mảng[][];
Dạng 2:
[Kiểu_dữ_liệu][][] Tên_mảng;
trong đó: [Kiểu_dữ_liệu] mô tả kiểu của mỗi phần tử thuộc mảng (như int, char, double, String,...), tên_mảng là tên của mảng và quy tắc đặt tên phải tuân theo quy tắc đặt tên biến trong Java.
Ví dụ: int a[][];: khai báo mảng hai chiều a có kiểu dữ liệu là int.
Cấp phát bộ nhớ cho mảng
Để cấp phát bộ nhớ cho mảng 2 chiều thì chúng ta sử dụng từ khóa new, trong đó [Số_dòng], [Số_cột]: là hai số nguyên dương chỉ ra số lượng dòng và số lượng cột của mảng hai chiều và trong Java có 2 cách để cấp phát bộ nhớ như sau:
Cách 1:
[Kiểu_dữ_liệu] Tên_mảng[][] = new [Kiểu_dữ_liệu] [Số_dòng][Số_cột];
Ví dụ: khai báo và cấp phát bộ nhớ cho mảng number có 2 dòng, 3 cột:
int number[][] = new int[2][3];
Cách 2:
[Kiểu_dữ_liệu][][] Tên_mảng = new [Kiểu_dữ_liệu] [Số_dòng][Số_cột];
Ví dụ: khai báo và cấp phát bộ nhớ cho mảng A có 3 dòng, 5 cột:
String[][] A = new String[3][5];
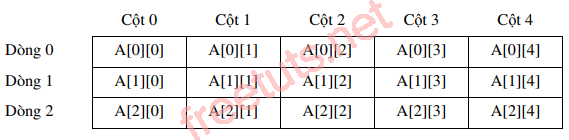
Khi trình biên dịch gặp lệnh trên thì nó sẽ cấp phát vùng nhớ để chứa mảng hai chiều có 3 dòng, 5 cột với số phần tử trong mảng = số dòng * số cột = 15. Hình ảnh minh họa của mảng hai chiều trên như là một bảng gồm có các dòng và các cột như sau:
Bản chất của mảng 2 chiều là mỗi dòng của nó chính là một mảng một chiều. Ví dụ: với mảng hai chiều a có 3 dòng, 5 cột, mỗi phần tử của mảng có kiểu int thì a được xem như mảng một chiều có 3 phần tử, mỗi phần tử này là một mảng một chiều có 5 phần tử.
Ngoài ra, Java còn cho phép chúng ta vừa có thể khai báo mảng và vừa khởi tạo giá trị cho mảng. Ví dụ để khai báo mảng một chiều có tên là diem, kiểu dữ liệu là int và mảng này chứa 6 phần tử có giá trị lần lượt là 1, 2, 3, 4, 5, 6 thì chúng ta làm như sau:
// khai báo một mảng 2 chiều có 3 dòng và 2 cột
int diem[][] = {{1, 2}, {3, 4}, {5, 6}};Bảng dưới đây minh họa mảng hai chiều trên:
| Dòng | Cột | |
|---|---|---|
| 0 | 1 | |
| 0 | 1 | 2 |
| 1 | 3 | 4 |
| 2 | 5 | 6 |
Truy xuất các phần tử của mảng
Mỗi phần tử của mảng 2 chiều được truy xuất thông qua tên mảng cùng với chỉ số dòng và chỉ số cột của phần tử đó. Tương tự như mảng một chiều, nếu một mảng hai chiều có m dòng và n cột thì chỉ số của dòng sẽ chạy từ 0, 1, 2,..., m - 1 và chỉ số của cột sẽ chạy từ 0, 1, 2,..., n - 1.
Cú pháp như sau:
Tên_mảng[Chỉ_số_dòng][Chỉ_số_cột]
Ví dụ: Để truy cập đến phần tử nằm ở dòng 2, cột 1 của mảng diem được khai báo ở trên thì chúng ta làm như sau:
public static void main(String[] args) {
// khai báo một mảng 2 chiều có 3 dòng và 2 cột
int diem[][] = {{1, 2}, {3, 4}, {5, 6}};
System.out.println("Phần tử nằm ở dòng 2 và cột 1 trong mảng diem là " + diem[2][1]);
}
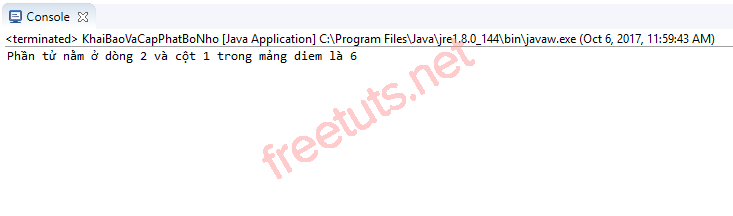
Nhìn vào bảng minh họa bên trên thì chúng ta nhận thấy phần tử nằm ở dòng 2 và cột 1 trong bảng diem là 6. Kết quả biên dịch chương trình cũng cho chúng ta thấy được điều đó:
2. Nhập xuất các phần tử cho mảng
Chương trình dưới đây sẽ minh họa cách nhập các phần tử cho mảng hai chiều từ bàn phím và sau đó hiển thị các phần tử đó ra màn hình.
public static void main(String[] args) {
// khai báo số dòng và số cột cho mảng
int soDong, soCot;
Scanner scanner = new Scanner(System.in);
System.out.println("Nhập vào số dòng của mảng: ");
soDong = scanner.nextInt();
System.out.println("Nhập vào số cột của mảng: ");
soCot = scanner.nextInt();
// khai báo và cấp phát bộ nhớ cho mảng
int[][] A = new int[soDong][soCot];
// Để nhập giá trị các phần tử cho mảng
// chúng ta sẽ sử dụng 2 vòng lặp for
// vòng lặp for bên ngoài sẽ duyệt i từ 0 đến soDong - 1
// và vòng lặp for bên trong sẽ duyệt j từ 0 đến soCot - 1
// mỗi lần như vậy thì sẽ nhập vào phần tử tại vị trí i, j
for (int i = 0; i < soDong; i++) {
for (int j = 0; j < soCot; j++) {
System.out.print("Nhập phần tử thứ [" + i + ", " + j + "]: ");
A[i][j] = scanner.nextInt();
}
}
// hiển thị các phần tử trong mảng vừa nhập
// chúng ta cũng sử dụng 2 vòng lặp for như khi nhập
System.out.println("Mảng vừa nhập: ");
for (int i = 0; i < soDong; i++) {
for (int j = 0; j < soCot; j++) {
System.out.print(A[i][j] + "\t");
}
// sau khi viết xong 1 dòng thi xuống hàng
System.out.println("\n");
}
}
Kết quả sau khi biên dịch chương trình:
3. Một số ví dụ về thao tác đối với mảng hai chiều
Ví dụ 1
Viết chương trình thực hiện các công việc sau:
- Nhập m, n là số dòng và 2 số cột của 2 ma trận 2 chiều A và B từ bàn phím.
- Nhập giá trị cho các phần tử cho 2 ma trận này.
- Tính và in ra màn hình ma trận C là tổng của 2 ma trận này.
Yêu cầu kỹ thuật: Kiểm tra số dòng, số cột nhập vào không được nhỏ hơn 1.
public static void main(String[] args) {
int m; // số dòng của ma trận
int n; // số cột của ma trận
Scanner scanner = new Scanner(System.in);
do {
System.out.println("Nhập vào số dòng của ma trận:");
m = scanner.nextInt();
System.out.println("Nhập vào số cột của ma trận:");
n = scanner.nextInt();
} while (m < 1 || n < 1);
// khai báo 2 ma trận A và B có m dòng và n cột
int A[][] = new int[m][n];
int B[][] = new int[m][n];
// ma trận tổng C
int C[][] = new int [m][n];
System.out.println("Nhập các phần tử cho ma trận A:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print("A[" + i + "," + j + "] = ");
A[i][j] = scanner.nextInt();
}
}
System.out.println("Nhập các phần tử cho ma trận B:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print("B[" + i + "," + j + "] = ");
B[i][j] = scanner.nextInt();
}
}
System.out.println("Ma trận A:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(A[i][j] + "\t");
}
System.out.println("\n");
}
System.out.println("Ma trận B:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(B[i][j] + "\t");
}
System.out.println("\n");
}
// Để tính tổng hai ma trận
// ta sẽ sử dụng 2 vòng lặp for
// để duyệt i từ 0 đến m và j từ 0 đến n
// sau đó tính tổng hai phần tử
// tại vị trí i, j tương ứng của 2 ma trận A, B
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
// hiển thị ma trận tổng C
System.out.println("Ma trận tổng C:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(C[i][j] + "\t");
}
System.out.println("\n");
}
}
Kết quả sau khi biên dịch chương trình:
Ví dụ 2
Một ma trận được gọi là ma trận thưa nếu số phần tử có giá trị bằng 0 nhiều hơn số phần tử khác 0. Viết chương trình thực hiện các công việc sau:
- Nhập m, n là số dòng và số cột của ma trận hai chiều A từ bàn phím.
- Nhập giá trị các phần tử của ma trận A từ bàn phím.
- Kiểm tra và thông báo lên màn hình ma trận vừa nhập là ma trận thưa hay ma trận không thưa.
Yêu cầu kỹ thuật: Kiểm tra số dòng, số cột nhập vào không được nhỏ hơn 1.
public static void main(String[] args) {
int m, n;
int soPhanTu0 = 0; // số phần tử = 0 trong ma trận
int soPhanTuKhac0 = 0; // số phần tử khác 0 trong ma trận
Scanner scanner = new Scanner(System.in);
do {
System.out.println("Nhập vào số dòng của ma trận:");
m = scanner.nextInt();
System.out.println("Nhập vào số cột của ma trận:");
n = scanner.nextInt();
} while (m < 1 || n < 1);
// khai báo ma trận A có m dòng, n cột
int A[][] = new int[m][n];
System.out.println("Nhập các phần tử cho ma trận A:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print("A[" + i + "," + j + "] = ");
A[i][j] = scanner.nextInt();
}
}
System.out.println("Ma trận A vừa nhập:");
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(A[i][j] + "\t");
}
System.out.println("\n");
}
// kiểm tra ma trận thưa hay không thưa
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// kiểm tra nếu phần tử tại i, j bằng 0
// thì tăng biến soPhanTu0 lên 1
// ngược lại tăng biến soPhanTuKhac0 lên 1
if (A[i][j] == 0) {
soPhanTu0++;
} else {
soPhanTuKhac0++;
}
}
}
// nếu biến soPhanTu0 lớn hơn soPhanTuKhac0
// thì ma trận đó là ma trận thưa
// ngược lại là ma trận không thưa
if (soPhanTu0 > soPhanTuKhac0) {
System.out.println("Ma trận vừa nhập là ma trận thưa");
} else {
System.out.println("Ma trận vừa nhập là ma trận không thưa");
}
}
Kết quả sau khi biên dịch chương trình:
Ví dụ 3
Một ma trận được gọi là ma trận đối xứng trước hết nó phải là ma trận vuông (có số dòng và số cột bằng nhau) và các phần tử của nó đối xứng nhau qua đường chéo chính. Viết chương trình nhập từ bàn phím các phần tử của ma trận A, kích thước m dòng, n cột (1 <= m, n <= 5). Kiểm tra xem ma trận vừa nhập có phải là ma trận đối xứng hay không?
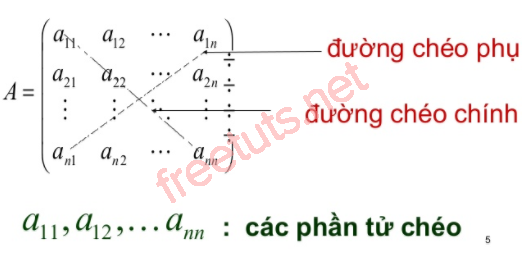
Hướng dẫn: Giả sử chúng ta có một ma trận vuông có 3 dòng, 3 cột thì chúng ta gọi ma trận này là ma trận vuông bậc 3. Hình dưới đây minh họa đường chéo phụ và đường chéo chính như sau:
Các phần tử nằm trên đường chéo chính có đặc điểm chỉ số dòng bằng chỉ số cột. Ví dụ trong hình trên chúng ta thấy có các phần tử nằm trên đường chéo chính như a11, a12,..., ann, các phần tử này được gọi là các phần tử chéo.
Để kiểm tra ma trận A có phải là ma trận đối xứng hay không thì cần thực hiện các bước sau:
- Ma trận A nhập vào phải luôn luôn là một ma trận vuông.
- Kiểm tra phần tử nằm dưới đường chéo chính có bằng phần tử đối xứng với nó qua đường chéo chính hay không (tức là kiểm tra các phần tử A[i][j] có bằng A[j][i] không, với i, j chạy từ 0 đến n).
public static void main(String[] args) {
int n; // bậc của ma trận
int kt = 0;
Scanner scanner = new Scanner(System.in);
do {
System.out.println("Nhập vào số bậc của ma trận: ");
n = scanner.nextInt();
} while (n < 1);
// ma trận A là ma trận vuông
// có n dòng và n cột
int[][] A = new int[n][n];
System.out.println("Nhập các phần tử cho ma trận A:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print("A[" + i + "," + j + "] = ");
A[i][j] = scanner.nextInt();
}
}
System.out.println("Ma trận A vừa nhập:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(A[i][j] + "\t");
}
System.out.println("\n");
}
// kiểm tra các phần tử nằm dưới đường chéo chính
// và phần tử đối xứng với nó qua đường chéo chính
// có bằng nhau hay không
// nếu bằng nhau thì ma trận đó là ma trận đối xứng
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (A[i][j] == A[j][i]) {
kt = 1;
} else {
kt = 0;
}
}
}
if (kt == 1) {
System.out.println("Ma trận vừa nhập là ma trận đối xứng");
} else {
System.out.println("Ma trận vừa nhập là ma trận không đối xứng");
}
}
Giải thích hoạt động của chương trình trên như sau:
Giả sử khi biên dịch chương trình, tôi nhập vào một ma trận vuông bậc 3 như sau:
3 1 2
1 0 3
Thì chúng ta thấy các phần tử nằm trên đường chéo chính bao gồm 3 phần tử đó là A00 = 3, A11 = 0 và A22 = 0. Hoạt động của vòng lặp for kiểm tra mảng đó có phải là mảng đối xứng trải qua các bước như sau:
Bước 1: Khởi tạo i = 0 < n nhưng j = 0 = i nên không thực hiện lệnh trong thân vòng lặp for.
Bước 2: Tăng i lên 1, lúc này i = 1 < n và j = 0 < i nên thực hiện lệnh trong thân vòng lặp for thì thấy A[1][0] = A[0][1] = 1 nên lúc này biến kt = 1.
Bước 3: Tăng j lên 1, lúc này j = 1 = i nên không thực hiện lệnh trong thân vòng lặp for.
Bước 4: Quay lại vòng lặp for, lúc này i = 2 < n và j = 0 < i nên thực hiện lệnh trong thân vòng lặp for thì thấy A[2][0] = A[0][2] = 2 nên lúc này biến kt = 1.
Bước 5: Tăng j lên 1, lúc này j = 1 < i nên thực hiện lệnh trong thân vòng lặp for thì thấy A[2][1] = A[1][2] = 3 nên lúc này biến kt = 1.
Bước 6: Tăng j lên 1, lúc này j = 2 = i nên không thực hiện lệnh trong thân vòng lặp for.
Bước 7: Tăng i lên 1, lúc này i = 3 = n nên kết thúc vòng lặp for.
for thì lúc này biến kt = 1 nên sẽ hiển thị thông báo "Ma trận vừa nhập là ma trận đối xứng" ra màn hình.4. Hạn chế của mảng
Vì các phần tử trong mảng được sắp xếp liên tục nên việc chèn hoặc xóa một phần tử trong mảng cũng sẽ gặp nhiều khó khăn.
5. Lời kết
Đây là bài cuối cùng về mảng và cũng là bài cuối cùng trong chương Chuỗi và mảng. Sang chương sau, chúng ta sẽ bước sang tìm hiểu một khái niệm mới dùng để giải quyết những hạn chế của mảng - đó là khái niệm Collections (Tập hợp) trong Java. Các bạn theo dõi nhé!
Câu hỏi thường gặp liên quan:
- Java - Tìm giá trị lớn nhất trong một ma trận 2 chiều với các phần tử được nhập từ bàn phím.
- Java - Viết chương trình tính tổng các phần tử nằm trên đường chéo chính của một ma trận vuông.
- Java - Tìm phần tử có giá trị lớn nhất và nhỏ nhất trên đường chéo chính của một ma trận vuông.
- Java - Thực hiện phép nhân hai ma trận và tìm ma trận chuyển vị của ma trận tích vừa tính được.
- Java - Thực hiện nhập vào một ma trận vuông và kiểm tra ma trận đó có phải là ma trận tam giác trên không?
- Java - Viết chương trình tính giá trị trung bình của các phần tử nhỏ nhất trên mỗi cột của một ma trận.
- Java - Viết chương trình tìm và in ra màn hình phần tử lớn nhất và vị trí của phần tử đó trong ma trận số nguyên
- Java - Viết chương trình tìm và in ra phần tử chẵn dương nhỏ nhất trong ma trận.
- Java - Viết chương trình xóa dòng có tổng lớn nhất của một ma trận số thực.

 Các kiểu dữ liệu trong C ( int - float - double - char ...)
Các kiểu dữ liệu trong C ( int - float - double - char ...)  Thuật toán tìm ước chung lớn nhất trong C/C++
Thuật toán tìm ước chung lớn nhất trong C/C++  Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành)  ComboBox - ListBox trong lập trình C# winforms
ComboBox - ListBox trong lập trình C# winforms  Random trong Python: Tạo số random ngẫu nhiên
Random trong Python: Tạo số random ngẫu nhiên  Lệnh cin và cout trong C++
Lệnh cin và cout trong C++  Cách khai báo biến trong PHP, các loại biến thường gặp
Cách khai báo biến trong PHP, các loại biến thường gặp  Download và cài đặt Vertrigo Server
Download và cài đặt Vertrigo Server  Thẻ li trong HTML
Thẻ li trong HTML  Thẻ article trong HTML5
Thẻ article trong HTML5  Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên  Cách dùng thẻ img trong HTML và các thuộc tính của img
Cách dùng thẻ img trong HTML và các thuộc tính của img  Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng