Các kiểu dữ liệu trong C ( int - float - double - char ...) 
Thuật toán tìm ước chung lớn nhất trong C/C++ 
Cấu trúc lệnh switch case trong C++ (có bài tập thực hành) 
Random trong Python: Tạo số random ngẫu nhiên 
Lệnh cin và cout trong C++ 
ComboBox - ListBox trong lập trình C# winforms 
Cách khai báo biến trong PHP, các loại biến thường gặp 
Download và cài đặt Vertrigo Server 
Thẻ li trong HTML 
Thẻ article trong HTML5 
Cấu trúc HTML5: Cách tạo template HTML5 đầu tiên 
Cách dùng thẻ img trong HTML và các thuộc tính của img 
Thẻ a trong HTML và các thuộc tính của thẻ a thường dùng Thông báo: Download 4 khóa học Python từ cơ bản đến nâng cao tại đây.
Hàm round() trong Python
Trong lập trình Python, việc làm tròn số là một thao tác quan trọng giúp xử lý các giá trị số một cách hiệu quả và chính xác. Hàm round() trong Python là công cụ mạnh mẽ và tiện lợi để làm tròn số theo nhiều cách khác nhau, đáp ứng các yêu cầu cụ thể của từng bài toán. Trong bài viết này, bạn sẽ học cách sử dụng hàm round() của Python để làm tròn số một cách chính xác và linh hoạt, bao gồm các tình huống làm tròn đơn giản cũng như phức tạp.
Giới thiệu về hàm round() của Python
Làm tròn số có nghĩa là làm cho số đó đơn giản hơn nhưng vẫn giữ giá trị gần với giá trị ban đầu. Ví dụ, số 89 làm tròn đến số gần nhất là 90 vì 89 gần 90 hơn 80.
Để làm tròn một số trong Python, bạn sử dụng hàm tích hợp round():
round(number [, ndigits])
Hàm round() làm tròn số đến bội số gần nhất của 10^(-ndigits).
Bài viết này được đăng tại [free tuts .net]
Nói cách khác, hàm round() trả về số được làm tròn đến độ chính xác ndigits sau dấu thập phân.
Nếu ndigits bị bỏ qua hoặc là None, hàm round() sẽ trả về số nguyên gần nhất.
Ví dụ về hàm round() của Python
Hãy xem một số ví dụ để hiểu rõ hơn về hàm round().
Ví dụ về hàm round() của Python
Ví dụ sau sử dụng hàm round() mà không truyền tham số ndigits:
round(1.25)
Kết quả:
1
Nó trả về số nguyên 1.
Tuy nhiên, nếu bạn truyền ndigits là 0, hàm round() sẽ trả về số float 1.0:
round(1.25, 0)
Kết quả:
1.0
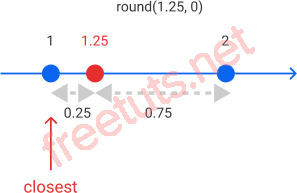
Khi ndigits là 0, hàm round() làm tròn số 1.25 đến bội số gần nhất của 10^(0) = 1.
Ví dụ sử dụng hàm round() với ndigits âm
round(15.5, -1)
Vì ndigits là -1, hàm round() làm tròn số 15.5 đến bội số gần nhất của 20 (10^-(-1)):
Kết quả:
20
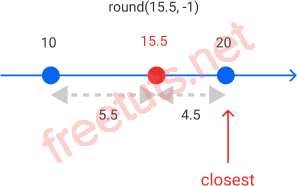
Vì ndigits là -1, hàm round() làm tròn số 15.5 đến bội số gần nhất của 20 (10^-(-1)).
Ví dụ về hàm round() của Python với trường hợp ties
Khi bạn làm tròn một số nằm giữa hai số, Python không thể tìm số gần nhất. Trong trường hợp này, Python sử dụng tiêu chuẩn IEEE 754 để làm tròn, gọi là "banker’s rounding".
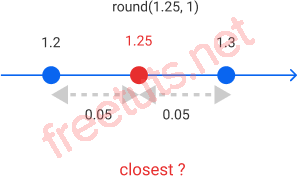
Trong banker’s rounding, số được làm tròn đến giá trị gần nhất, với các trường hợp ties được làm tròn đến giá trị gần nhất có chữ số cuối cùng là số chẵn.
Ví dụ:
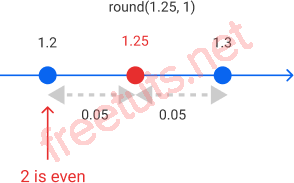
round(1.25, 1)
Kết quả:
1.2
Vì chữ số ít quan trọng nhất của 1.2 là 2, và 2 là số chẵn.
Tương tự, làm tròn số 1.35 sẽ trả về 1.4:
round(1.35, 1)
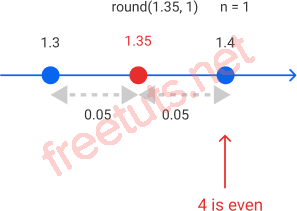
Python sử dụng banker’s rounding thay vì làm tròn ra khỏi số 0 vì nó ít thiên vị hơn.
Ví dụ, nếu bạn tính trung bình ba số 1.5, 2.5, và 3.5, làm tròn ra khỏi số 0 trả về 3.0 trong khi banker’s rounding trả về 2.66:
| Số | Banker’s Rounding | Làm tròn ra khỏi số 0 |
|---|---|---|
| 1.5 | 2 | 2 |
| 2.5 | 2 | 3 |
| 3.5 | 4 | 4 |
| Trung bình | 2.66666… | 3.0 |
Cách làm tròn ra khỏi số 0 trong Python
Python không cung cấp cách trực tiếp để làm tròn số ra khỏi số 0 như bạn có thể mong đợi. Ví dụ:
| Số | Làm tròn ra khỏi số 0 |
|---|---|
| 1.2 | 1 |
| 1.5 | 2 |
Một cách phổ biến để làm tròn số ra khỏi số 0 là sử dụng biểu thức sau:
int(x + 0.5)
Biểu thức này hoạt động đúng cho các số dương. Ví dụ:
print(int(1.2 + 0.5)) print(int(1.5 + 0.5))
Kết quả:
1 2
Tuy nhiên, nó không hoạt động đúng cho các số âm:
print(int(-1.2 + 0.5)) print(int(-1.5 + 0.5))
Kết quả:
0 -1
Đối với các số âm, bạn nên trừ đi 0.5 thay vì cộng thêm.
Ví dụ sau hoạt động đúng cho các số âm:
print(int(-1.2 - 0.5)) print(int(-1.5 - 0.5))
Bạn có thể định nghĩa một hàm trợ giúp để làm tròn một số:
def round_up(x):
if x > 0:
return int(x + 0.5)
return int(x - 0.5)
Mô-đun math của Python cung cấp cho bạn một hàm gọi là copysign():
math.copysign(x, y)
Hàm copysign() trả về giá trị tuyệt đối của x nhưng giữ dấu của y.
Bạn có thể sử dụng hàm copysign() để phát triển hàm round_up() mà không cần kiểm tra x là dương hay âm:
from math import copysign
def round_up(x):
return int(x + copysign(0.5, x))
Kết bài
Việc làm tròn số là một thao tác thường gặp và cần thiết trong lập trình, đặc biệt khi xử lý các giá trị số thực. Hàm round() của Python cung cấp một phương thức linh hoạt và hiệu quả để làm tròn số, giúp bạn dễ dàng điều chỉnh mức độ chính xác theo yêu cầu. Qua hướng dẫn này, bạn đã nắm được cách sử dụng hàm round() cùng các trường hợp đặc biệt và phức tạp. Hãy áp dụng những kiến thức này vào các bài toán thực tế để xử lý số liệu một cách chính xác và hiệu quả hơn.
